4.2.2.1指数函数的图象和性质(一)(共25张PPT)
文档属性
| 名称 | 4.2.2.1指数函数的图象和性质(一)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 578.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 13:18:09 | ||
图片预览






文档简介
(共25张PPT)
第四章
4.2.2 指数函数的图象和性质
第一课时 指数函数的图象和性质(一)
1.掌握指数函数的图象及简单性质.
2.掌握利用指数函数的图象和性质求函数的定义域和值域.
课标要求
素养要求
1.通过借助计算工具画出简单指数函数的图象,发展直观想象素养.
2.通过指数性质的应用提升数学运算素养.
课前预习
知识探究
1
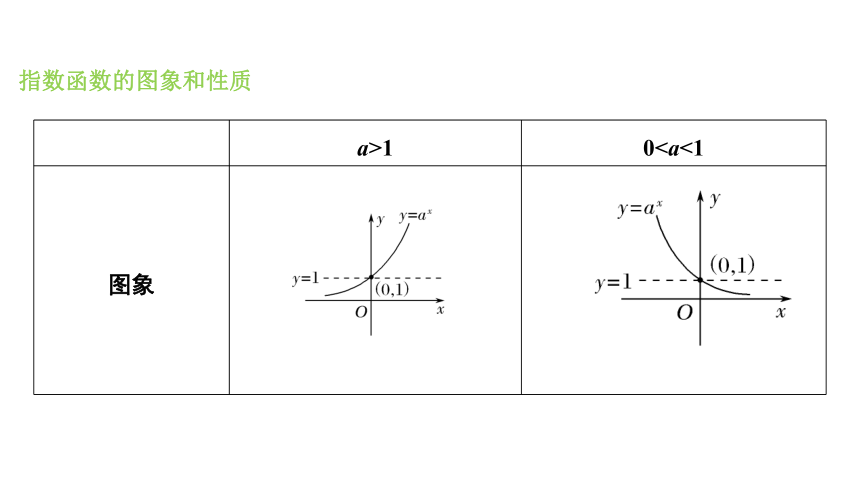
指数函数的图象和性质
a>1 0图象
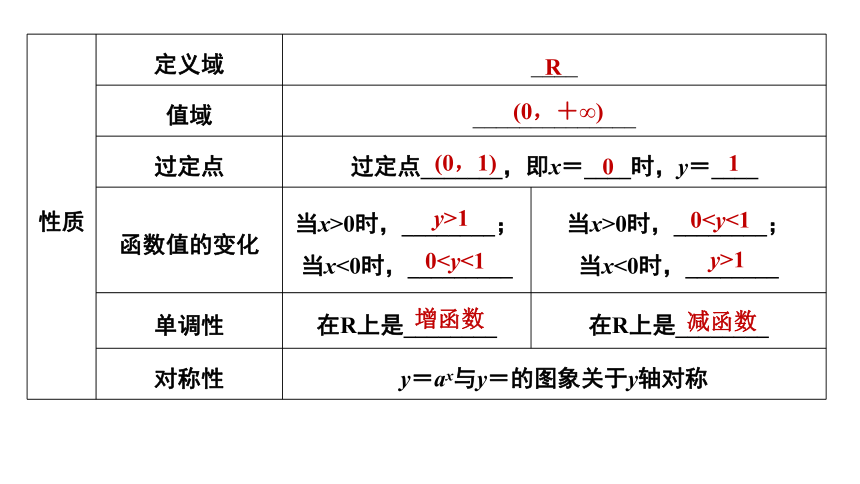
性质 定义域 ____ 值域 ______________ 过定点 过定点_______,即x=____时,y=____ 函数值的变化 当x>0时,________; 当x<0时,_________ 当x>0时,________;
当x<0时,________
单调性 在R上是________ 在R上是________
对称性 y=ax与y=的图象关于y轴对称 R
(0,+∞)
(0,1)
0
1
y>1
00y>1
增函数
减函数
点睛
(1)当a>1时,x→-∞,y→0;当0(2)底数互为倒数的两个指数函数的图象关于y轴对称,根据这种对称性,就可以利用一个函数的图象画出另一个函数的图象.
(3)在y轴右侧,图象从上到下相应的底数由大变小,即“底数大图象高”;
在y轴左侧,图象从上到下相应的底数由小变大,即“底数大图象低”.
1.思考辨析,判断正误
(1)若函数y=(a-3)x是增函数,则a>4.( )
(2)函数f(x)=a|x-2|是偶函数.( )
提示 函数f(x)=a|x-2|的图象是由y=a|x|的图象向右平移2个单位得到的,其图象不关于y轴对称,故(2)错.
(3)函数f(x)=2x的图象与g(x)=-2x的图象关于x轴对称.( )
√
×
√
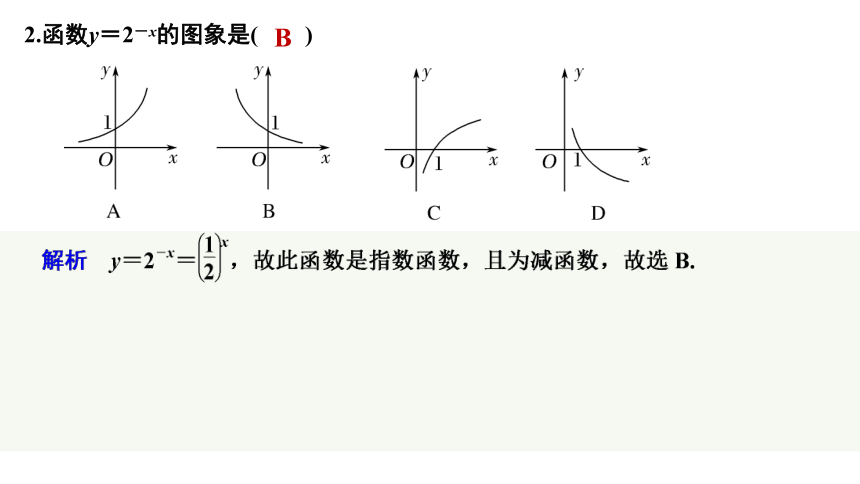
2.函数y=2-x的图象是( )
B
3.指数函数y=2x的定义域是________,值域是___________.
R
解析 由指数函数y=2x的图象和性质可知定义域为R,值域为(0,+∞).
(0,+∞)
(0,1)
解析 由题意知当x≤0时,ax-1≥0,
那么ax≥1,所以0课堂互动
题型剖析
2
题型一 与指数函数有关的定义域和值域问题
【例1】 求下列函数的定义域和值域:
1.y=af(x)型函数的定义域、值域的求法
(1)形如y=af(x)的函数的定义域就是f(x)的定义域.
(2)形如y=af(x)的函数的值域,先求出u=f(x)的值域,再结合y=au的单调性求出y=af(x)的值域.若a的取值范围不确定,则需对a进行分类讨论.
2.y=f(ax)型函数的定义域、值域的求法
(1)函数y=f(ax)(a>0且a≠1)的定义域,关键是找出t=ax的值域的哪些部分在y=f(x)的定义域中;
(2)求函数y=f(ax)的值域,先求出t=ax的值域,再求y=f(x)的值域.
思维升华
【训练1】 (多选题)下列函数的值域不是(0,+∞)的有( )
ABD
【例2】 (1)函数f(x)=2ax+1-3(a>0,且a≠1)的图象恒过的定点是__________.
题型二 指数函数的图象
解析 因为y=ax的图象过定点(0,1),所以令x+1=0,
即x=-1,则f(x)=-1,故f(x)=2ax+1-3的图象过定点(-1,-1).
(-1,-1)
处理函数图象问题的策略
(1)抓住特殊点:指数函数的图象过定点(0,1),求指数型函数图象所过的定点时,只要令指数为0,求出对应的y的值,即可得函数图象所过的定点.
(2)巧用图象变换:函数图象的平移变换(左右平移、上下平移).
(3)利用函数的性质:奇偶性与单调性.
思维升华
【训练2】 (1)函数y=2|x|的图象是( )
B
(2)函数y=ax,y=x+a在同一坐标系中的图象可能是( )
解析 由题意知a>0且a≠1,则函数y=x+a单调递增.当01时,y=ax单调递增,直线y=x+a在y轴上的截距大于1.故选D.
D
题型三 指数函数图象的应用
C
φ(x)=ax的图象,如图所示,
当0图象法解方程和不等式问题
利用函数的图象可解决与方程和不等式有关的问题,如观察两个函数y=f(x)和y=g(x)的图象的交点个数可确定方程f(x)=g(x)的解的个数,观察函数y=f(x)的图象与x轴的交点情况,可以确定不等式f(x)>0或f(x)<0的解集等.
思维升华
【训练3】 (1)指数函数①y=ax,②y=bx,③y=cx,④y=dx在同一坐标系中的图象如图,根据图象可得a,b,c,d与1的大小关系为( )
A.aC.1B
解析 如图,直线x=1与四条曲线的交点坐标从下往上依次是(1,b),(1,a),(1,d),(1,c),故有0(2)若函数y=|2x-1|在(-∞,m]上单调递减,则m的取值范围是__________.
(-∞,0]
解析 (2)画出y=2x的图象,沿y轴向下平移1个单位长度得到y=2x-1的图象,再将图象在x轴下方的部分沿x轴翻折,其余部分不变,如图.由图知y=|2x-1|在(-∞,0]上单调递减,∴m∈(-∞,0].
1.对于形如y=af(x)与y=f(ax)的函数,求其定义域和值域要利用换元的思想方法,结合函数的单调性求解.
2.作指数函数的图象,要抓住其单调性,过定点等特征,并结合图象的平移、翻折等变换规则进行.
课堂小结
第四章
4.2.2 指数函数的图象和性质
第一课时 指数函数的图象和性质(一)
1.掌握指数函数的图象及简单性质.
2.掌握利用指数函数的图象和性质求函数的定义域和值域.
课标要求
素养要求
1.通过借助计算工具画出简单指数函数的图象,发展直观想象素养.
2.通过指数性质的应用提升数学运算素养.
课前预习
知识探究
1
指数函数的图象和性质
a>1 0
性质 定义域 ____ 值域 ______________ 过定点 过定点_______,即x=____时,y=____ 函数值的变化 当x>0时,________; 当x<0时,_________ 当x>0时,________;
当x<0时,________
单调性 在R上是________ 在R上是________
对称性 y=ax与y=的图象关于y轴对称 R
(0,+∞)
(0,1)
0
1
y>1
0
增函数
减函数
点睛
(1)当a>1时,x→-∞,y→0;当0
(3)在y轴右侧,图象从上到下相应的底数由大变小,即“底数大图象高”;
在y轴左侧,图象从上到下相应的底数由小变大,即“底数大图象低”.
1.思考辨析,判断正误
(1)若函数y=(a-3)x是增函数,则a>4.( )
(2)函数f(x)=a|x-2|是偶函数.( )
提示 函数f(x)=a|x-2|的图象是由y=a|x|的图象向右平移2个单位得到的,其图象不关于y轴对称,故(2)错.
(3)函数f(x)=2x的图象与g(x)=-2x的图象关于x轴对称.( )
√
×
√
2.函数y=2-x的图象是( )
B
3.指数函数y=2x的定义域是________,值域是___________.
R
解析 由指数函数y=2x的图象和性质可知定义域为R,值域为(0,+∞).
(0,+∞)
(0,1)
解析 由题意知当x≤0时,ax-1≥0,
那么ax≥1,所以0
题型剖析
2
题型一 与指数函数有关的定义域和值域问题
【例1】 求下列函数的定义域和值域:
1.y=af(x)型函数的定义域、值域的求法
(1)形如y=af(x)的函数的定义域就是f(x)的定义域.
(2)形如y=af(x)的函数的值域,先求出u=f(x)的值域,再结合y=au的单调性求出y=af(x)的值域.若a的取值范围不确定,则需对a进行分类讨论.
2.y=f(ax)型函数的定义域、值域的求法
(1)函数y=f(ax)(a>0且a≠1)的定义域,关键是找出t=ax的值域的哪些部分在y=f(x)的定义域中;
(2)求函数y=f(ax)的值域,先求出t=ax的值域,再求y=f(x)的值域.
思维升华
【训练1】 (多选题)下列函数的值域不是(0,+∞)的有( )
ABD
【例2】 (1)函数f(x)=2ax+1-3(a>0,且a≠1)的图象恒过的定点是__________.
题型二 指数函数的图象
解析 因为y=ax的图象过定点(0,1),所以令x+1=0,
即x=-1,则f(x)=-1,故f(x)=2ax+1-3的图象过定点(-1,-1).
(-1,-1)
处理函数图象问题的策略
(1)抓住特殊点:指数函数的图象过定点(0,1),求指数型函数图象所过的定点时,只要令指数为0,求出对应的y的值,即可得函数图象所过的定点.
(2)巧用图象变换:函数图象的平移变换(左右平移、上下平移).
(3)利用函数的性质:奇偶性与单调性.
思维升华
【训练2】 (1)函数y=2|x|的图象是( )
B
(2)函数y=ax,y=x+a在同一坐标系中的图象可能是( )
解析 由题意知a>0且a≠1,则函数y=x+a单调递增.当0
D
题型三 指数函数图象的应用
C
φ(x)=ax的图象,如图所示,
当0
利用函数的图象可解决与方程和不等式有关的问题,如观察两个函数y=f(x)和y=g(x)的图象的交点个数可确定方程f(x)=g(x)的解的个数,观察函数y=f(x)的图象与x轴的交点情况,可以确定不等式f(x)>0或f(x)<0的解集等.
思维升华
【训练3】 (1)指数函数①y=ax,②y=bx,③y=cx,④y=dx在同一坐标系中的图象如图,根据图象可得a,b,c,d与1的大小关系为( )
A.a
解析 如图,直线x=1与四条曲线的交点坐标从下往上依次是(1,b),(1,a),(1,d),(1,c),故有0
(-∞,0]
解析 (2)画出y=2x的图象,沿y轴向下平移1个单位长度得到y=2x-1的图象,再将图象在x轴下方的部分沿x轴翻折,其余部分不变,如图.由图知y=|2x-1|在(-∞,0]上单调递减,∴m∈(-∞,0].
1.对于形如y=af(x)与y=f(ax)的函数,求其定义域和值域要利用换元的思想方法,结合函数的单调性求解.
2.作指数函数的图象,要抓住其单调性,过定点等特征,并结合图象的平移、翻折等变换规则进行.
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
