5.5.1第三课时 两角和与差的正切公式(共22张PPT)
文档属性
| 名称 | 5.5.1第三课时 两角和与差的正切公式(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 752.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 13:10:28 | ||
图片预览







文档简介
(共22张PPT)
第五章
第三课时 两角和与差的正切公式
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
课标要求
素养要求
从公式间的联系入手,引导学生对公式变形,感悟数学抽象的作用,提升逻辑推理、数学运算素养.
课前预习
知识探究
1
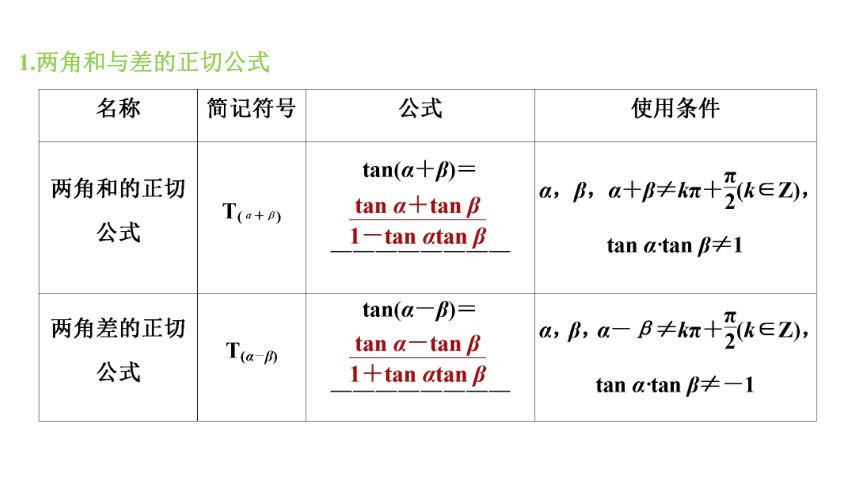
1.两角和与差的正切公式
2.两角和与差的正切公式的变形
(1)T(α+β)的变形:
tan α+tan β=________________________.
tan α+tan β+tan αtan βtan(α+β)=__________.
tan αtan β=______________.
(2)T(α-β)的变形:
tan α-tan β=_______________________.
tan α-tan β-tan αtan βtan(α-β)=__________.
tan αtan β=______________.
tan(α+β)(1-tan αtan β)
tan(α+β)
tan(α-β)(1+tan αtan β)
tan(α-β)
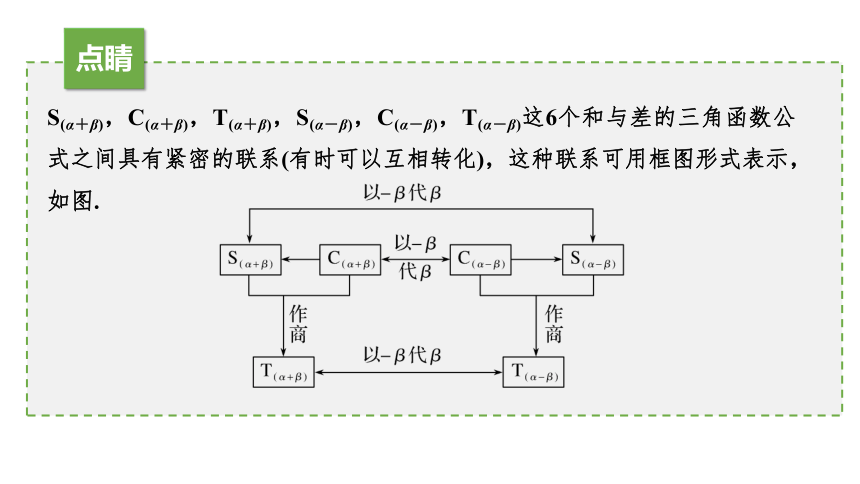
点睛
S(α+β),C(α+β),T(α+β),S(α-β),C(α-β),T(α-β)这6个和与差的三角函数公式之间具有紧密的联系(有时可以互相转化),这种联系可用框图形式表示,如图.
1.思考辨析,判断正误
(1)存在α,β∈R,使tan(α+β)=tan α+tan β成立.( )
√
×
×
2.(多选题)已知α,β为任意角,则下列等式恒成立的有( )
ABC
-3
课堂互动
题型剖析
2
题型一 公式的正用、逆用、变形用
A
-1
(3)∵tan 23°+tan 37°=tan 60°(1-tan 23°tan 37°),
思维升华
【训练1】 求值:
tan α+tan β=tan(α+β)(1-tan αtan β)得:
tan 10°+tan 35°=tan 45°(1-tan 10°tan 35°)=1-tan 10°tan 35,
所以tan 10°+tan 35°+tan 10°tan 35°=1.
(3)(1+tan 18°)(1+tan 27°)=1+tan 18°+tan 27°+tan 18°tan 27°
=1+tan 45°(1-tan 18°tan 27°)+tan 18°·tan 27°=2.
题型二 条件求值问题
解析 (1)由题意知tan α+tan β=3,tan α·tan β=2,
A
C
给值求值问题的两种变换
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系以实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角与待求角间的关系,如用α=β-(β-α),2α=(α+β)+(α-β)等关系,把待求的三角函数与已知三角函数巧妙地建立等量关系,从而求值.
思维升华
题型三 给值求角问题
(2)若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.
解 ∵(1-tan α)(1-tan β)=2,
∴1-(tan α+tan β)+tan αtan β=2,
∴tan α+tan β=tan αtan β-1,
探究利用公式T(α±β)求角的步骤
(1)求值:根据题设条件求角的某一三角函数值.
(2)确定所求角的范围(范围讨论的过大或过小,会使求出的角不合题意或漏解),根据范围找出角.
思维升华
C
课堂小结
第五章
第三课时 两角和与差的正切公式
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
课标要求
素养要求
从公式间的联系入手,引导学生对公式变形,感悟数学抽象的作用,提升逻辑推理、数学运算素养.
课前预习
知识探究
1
1.两角和与差的正切公式
2.两角和与差的正切公式的变形
(1)T(α+β)的变形:
tan α+tan β=________________________.
tan α+tan β+tan αtan βtan(α+β)=__________.
tan αtan β=______________.
(2)T(α-β)的变形:
tan α-tan β=_______________________.
tan α-tan β-tan αtan βtan(α-β)=__________.
tan αtan β=______________.
tan(α+β)(1-tan αtan β)
tan(α+β)
tan(α-β)(1+tan αtan β)
tan(α-β)
点睛
S(α+β),C(α+β),T(α+β),S(α-β),C(α-β),T(α-β)这6个和与差的三角函数公式之间具有紧密的联系(有时可以互相转化),这种联系可用框图形式表示,如图.
1.思考辨析,判断正误
(1)存在α,β∈R,使tan(α+β)=tan α+tan β成立.( )
√
×
×
2.(多选题)已知α,β为任意角,则下列等式恒成立的有( )
ABC
-3
课堂互动
题型剖析
2
题型一 公式的正用、逆用、变形用
A
-1
(3)∵tan 23°+tan 37°=tan 60°(1-tan 23°tan 37°),
思维升华
【训练1】 求值:
tan α+tan β=tan(α+β)(1-tan αtan β)得:
tan 10°+tan 35°=tan 45°(1-tan 10°tan 35°)=1-tan 10°tan 35,
所以tan 10°+tan 35°+tan 10°tan 35°=1.
(3)(1+tan 18°)(1+tan 27°)=1+tan 18°+tan 27°+tan 18°tan 27°
=1+tan 45°(1-tan 18°tan 27°)+tan 18°·tan 27°=2.
题型二 条件求值问题
解析 (1)由题意知tan α+tan β=3,tan α·tan β=2,
A
C
给值求值问题的两种变换
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系以实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角与待求角间的关系,如用α=β-(β-α),2α=(α+β)+(α-β)等关系,把待求的三角函数与已知三角函数巧妙地建立等量关系,从而求值.
思维升华
题型三 给值求角问题
(2)若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.
解 ∵(1-tan α)(1-tan β)=2,
∴1-(tan α+tan β)+tan αtan β=2,
∴tan α+tan β=tan αtan β-1,
探究利用公式T(α±β)求角的步骤
(1)求值:根据题设条件求角的某一三角函数值.
(2)确定所求角的范围(范围讨论的过大或过小,会使求出的角不合题意或漏解),根据范围找出角.
思维升华
C
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
