2021--2022学年人教版九年级数学上册24 .2.2 直线和圆的位置关系 复习课件(共29张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册24 .2.2 直线和圆的位置关系 复习课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 16:33:44 | ||
图片预览




文档简介
(共29张PPT)
24.2.2直线和圆的位置关系
复习课
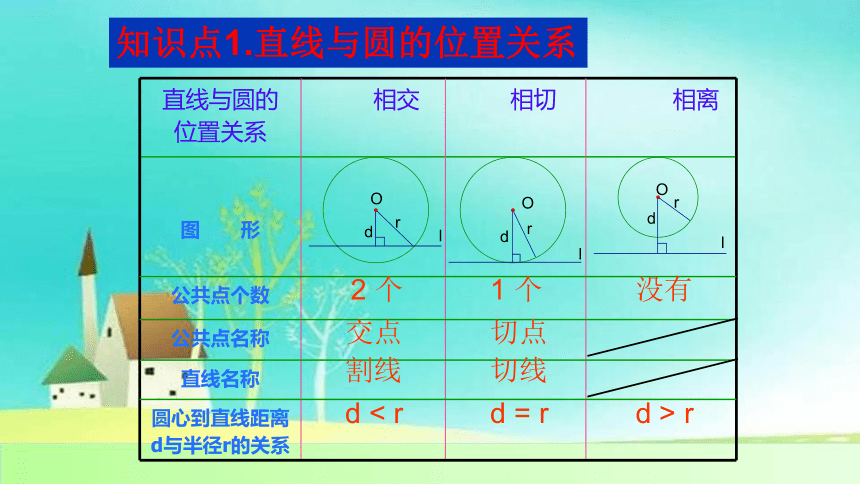
知识点1.直线与圆的位置关系
直线与圆的 位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
重要结论:判断直线与圆的位置关系
直线l与☉O 相交 d<r;
直线l与☉O 相切 d=r;
直线l与☉O 相离 d>r.
典例解析:
回顾例1.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的
圆与AB有怎样的位置关系 为什么
(1)r=2. (2)r=2.4. (3) r=3.
解:(1)当r=2时,AB和圆相离.
(2)当r=2.4时,AB和圆相切.
(3)当r=3时,AB和圆相交.
归纳总结:
判定直线与圆的位置关系,关键是先确定圆心到直线的距离(d)和圆的半径(r)两个量,然后再进行d与r的大小比较,最后根据d与r的数量关系得到直线与圆的位置关系.
d=CD=2.4
D
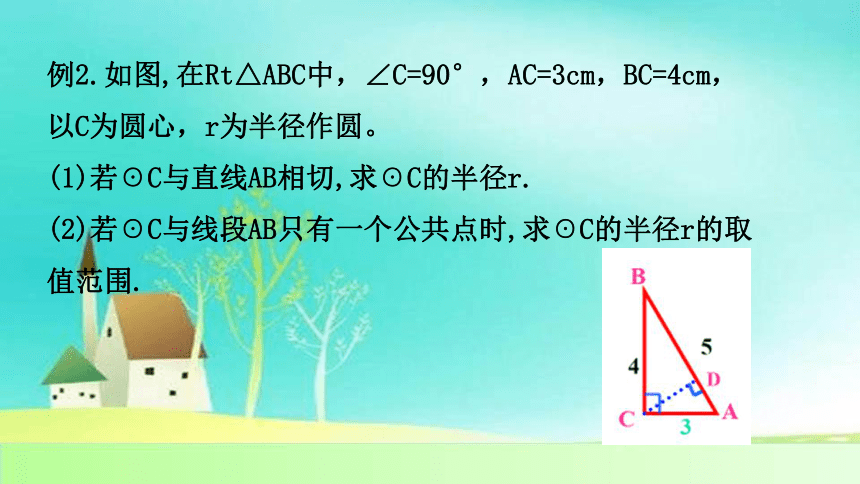
例2.如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
(1)若☉C与直线AB相切,求☉C的半径r.
(2)若☉C与线段AB只有一个公共点时,求☉C的半径r的取值范围.
B
C
A
D
4
5
3
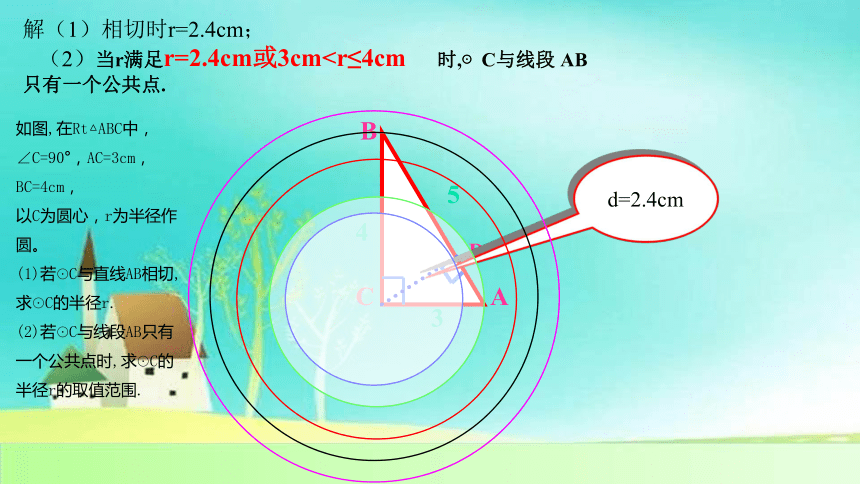
d=2.4cm
解(1)相切时r=2.4cm;
(2)当r满足r=2.4cm或3cm如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
(1)若☉C与直线AB相切,求☉C的半径r.
(2)若☉C与线段AB只有一个公共点时,求☉C的半径r的取值范围.
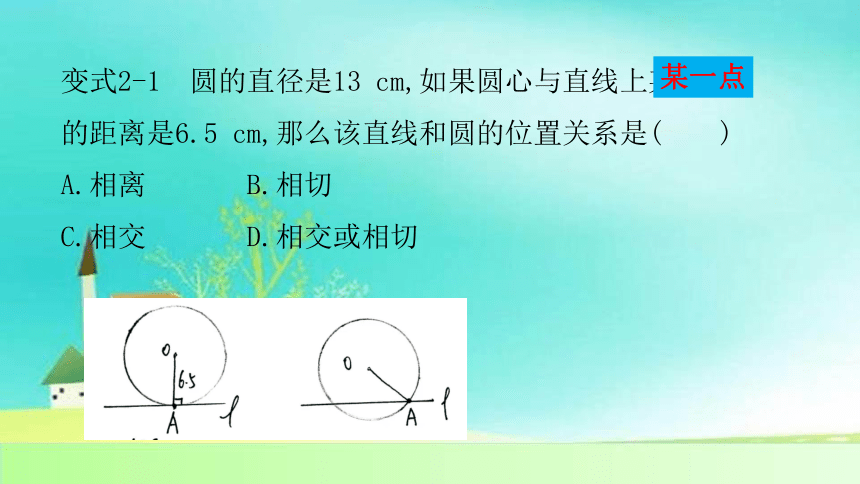
变式2-1 圆的直径是13 cm,如果圆心与直线上某一点的距离是6.5 cm,那么该直线和圆的位置关系是( )
A.相离 B.相切
C.相交 D.相交或相切
某一点
归纳总结:
首先根据直线与圆的位置关系,得到圆心到直线的距离(d)和圆的半径(r)的数量关系,再根据数量关系列出方程或不等式求解.
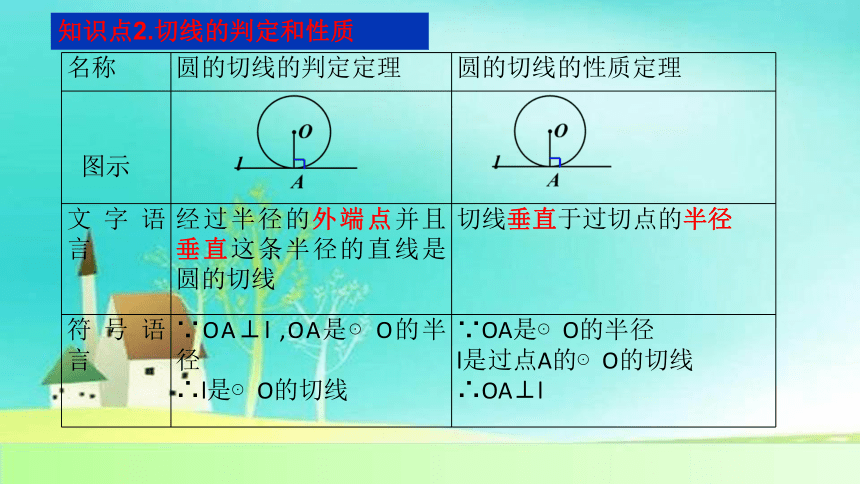
名称 圆的切线的判定定理 圆的切线的性质定理
图示
文字语言 经过半径的外端点并且垂直这条半径的直线是圆的切线 切线垂直于过切点的半径
符号语言 ∵OA⊥l ,OA是⊙O的半径 ∴l是⊙O的切线 ∵OA是⊙O的半径
l是过点A的⊙O的切线
∴OA⊥l
知识点2.切线的判定和性质
(1)切线长的定义:
切线上一点到切点之间的线段的长叫作这点到圆的切线长.
知识点
知识点3.切线长的概念和定理
(2)切线长定理:
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
特别提示:切线长定理包括线段相等和角相等两个结论,为证明线段相等、角相等提供了新的方法.
PA、PB是☉O的两条切线
PA = PB
∠OPA=∠OPB,∠AOP=∠BOP
几何语言:
例3(1)如图,点A在⊙O上,若∠ABO=∠P= 30°,
则直线PA与⊙O的位置关系是 .
变式3-1 设⊙O的半径为4,点O到直线a的距离为d,若⊙O
与直线a至少有一个公共点,则d为 .
例3.(2)已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。
E
例4.如图所示,△ABC是直角三角形,∠ABC=90°,
以AB为直径的☉O交AC于点E,点D是BC边的中点,连接DE.
(1)求证:DE与O相切;
(2)若O的半径为 ,DE=3,求AE.
总结归纳1:
证明一条切线的两种辅助线:
(1)若已知直线与圆有公共点,则连接圆心与公共点,证明已知直线与过公共点的半径垂直,简记为“已知圆上点,连半径,证垂直”.
(2)若已知直线与圆没有公共点,则过圆心作直线的垂线,证明圆心到直线的距离与圆的半径相等,简记为“未知圆上点,作垂直,证半径”.
口诀:已知圆上点,连半径,证垂直;
未知圆上点,作垂直,证半径。
归纳总结2:
在运用切线长定理时,要注意切线长定理与等腰三角形,勾股定理,垂径定理,切线的性质及圆中有关的性质定理等知识的联系与运用。
三三两两一直线
拓展:切线长定理的一个基本图形,包含的其他结论有:
(1)三组垂直线段:OA⊥PA,OB⊥PB,AB⊥OP;
(2)三组全等三角形:△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP;
(3)两组相等的弧: ;
(4)两个等腰三角形:△OAB,△PAB;
(5)一条特殊的直线:OP平分∠APB和∠AOB
例5.如图,AB为☉O的直径,C为☉O上的一点,AD和过
点C的切线互相垂直,垂足为D。求证:AC平分∠DAB。
变式5-1 如图,一个边长为4cm的等边△ABC的高与☉O的
直径相等, ☉O与BC相切于点C,与AC相交于点E,则
CE的长为 .
M
归纳总结:
当已知圆的切线和切点时,通常需要连接圆心和切点,可以得到
切线与半径垂直。充分运用切线的有关性质“两过一垂直”。
1.切线垂直于过切点的半径.
2.经过圆心垂直于切线的直线必过切点.
3.经过切点垂直于切线的直线必过圆心.
切线的性质:
以上关于切线的性质可归纳为:已知直线满足a.过圆心,b.过切点,c.垂直于切线中任意两个,便得到第三个结论.
两过一垂直
课堂小结
1.直线与圆的位置关系
2.切线的判定方法及其性质:
特别记忆:证切线时常用辅助线添加方法:
①已知圆上点,连半径,证垂直;
②已知圆上点,作垂直,证半径.
3.切线长定理及其简单应用。
2.如图,在△ABC中,AB=3,AC=4,BC=5,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是( )
A.相切 B.相交
C.相离 D.无法确定
复习检测(共五道题目,每题20分, 满分100分 )
1.如图:在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,则∠AOB = .
3.如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(-3,0),将☉P沿x轴的正方向平移,使得☉P与y轴相切,则平移的距离为( )
A.1 B.3 C.5 D.1或5
4.如图,已知PA、PB、EF分别切于A、B、D,若PA=15cm,则△PEF的周长是
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径.
O
知识点4:三角形的内切圆及内心的概念
名称 定义 图示
三角形的内切圆 与三角形的三边都相切的圆
三角形的内心 三角形内切圆的圆心,也是三角形内角平分线的交点 例6.(1) 如图,△ABC中,∠ B=43°,∠C=61 °,点I是
△ABC的内心,求∠ BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点I是△ABC的内心,
∴IB,IC分别是∠ B,∠C的平分线,
在△IBC中,
归纳总结:在解决三角形内切圆的相关问题时,常利用切线的性质,在直角三角形中借助方程来解决问题,或利用内心是角平分线的交点来进行角度的计算.
(2)在Rt△ABC中,AC=8,BC=6,则△ABC的
内切圆半径r = .
变式6-1 设△ABC的面积为S,周长为L, △ABC内切圆的半径为r,则S,L与r之间的数量关系是= .
变式6-2 ☉O 内切于四边形ABCD,AB=10,BC=7,
CD=8.求AD的长度。
知识拓展一:弦切角的定义及性质
1.定义:顶点在圆上,一边和圆相交,另一边和圆相切的叫弦切角。
2.弦切角定理:弦切角等于它所夹的弧所对的圆周角。
拓展应用1:如图,AB为☉O的直径,圆周角∠ ABC=40°,
当∠ BCD= °时,CD为☉O的切线。
24.2.2直线和圆的位置关系
复习课
知识点1.直线与圆的位置关系
直线与圆的 位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
重要结论:判断直线与圆的位置关系
直线l与☉O 相交 d<r;
直线l与☉O 相切 d=r;
直线l与☉O 相离 d>r.
典例解析:
回顾例1.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的
圆与AB有怎样的位置关系 为什么
(1)r=2. (2)r=2.4. (3) r=3.
解:(1)当r=2时,AB和圆相离.
(2)当r=2.4时,AB和圆相切.
(3)当r=3时,AB和圆相交.
归纳总结:
判定直线与圆的位置关系,关键是先确定圆心到直线的距离(d)和圆的半径(r)两个量,然后再进行d与r的大小比较,最后根据d与r的数量关系得到直线与圆的位置关系.
d=CD=2.4
D
例2.如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
(1)若☉C与直线AB相切,求☉C的半径r.
(2)若☉C与线段AB只有一个公共点时,求☉C的半径r的取值范围.
B
C
A
D
4
5
3
d=2.4cm
解(1)相切时r=2.4cm;
(2)当r满足r=2.4cm或3cm
以C为圆心,r为半径作圆。
(1)若☉C与直线AB相切,求☉C的半径r.
(2)若☉C与线段AB只有一个公共点时,求☉C的半径r的取值范围.
变式2-1 圆的直径是13 cm,如果圆心与直线上某一点的距离是6.5 cm,那么该直线和圆的位置关系是( )
A.相离 B.相切
C.相交 D.相交或相切
某一点
归纳总结:
首先根据直线与圆的位置关系,得到圆心到直线的距离(d)和圆的半径(r)的数量关系,再根据数量关系列出方程或不等式求解.
名称 圆的切线的判定定理 圆的切线的性质定理
图示
文字语言 经过半径的外端点并且垂直这条半径的直线是圆的切线 切线垂直于过切点的半径
符号语言 ∵OA⊥l ,OA是⊙O的半径 ∴l是⊙O的切线 ∵OA是⊙O的半径
l是过点A的⊙O的切线
∴OA⊥l
知识点2.切线的判定和性质
(1)切线长的定义:
切线上一点到切点之间的线段的长叫作这点到圆的切线长.
知识点
知识点3.切线长的概念和定理
(2)切线长定理:
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
特别提示:切线长定理包括线段相等和角相等两个结论,为证明线段相等、角相等提供了新的方法.
PA、PB是☉O的两条切线
PA = PB
∠OPA=∠OPB,∠AOP=∠BOP
几何语言:
例3(1)如图,点A在⊙O上,若∠ABO=∠P= 30°,
则直线PA与⊙O的位置关系是 .
变式3-1 设⊙O的半径为4,点O到直线a的距离为d,若⊙O
与直线a至少有一个公共点,则d为 .
例3.(2)已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。
E
例4.如图所示,△ABC是直角三角形,∠ABC=90°,
以AB为直径的☉O交AC于点E,点D是BC边的中点,连接DE.
(1)求证:DE与O相切;
(2)若O的半径为 ,DE=3,求AE.
总结归纳1:
证明一条切线的两种辅助线:
(1)若已知直线与圆有公共点,则连接圆心与公共点,证明已知直线与过公共点的半径垂直,简记为“已知圆上点,连半径,证垂直”.
(2)若已知直线与圆没有公共点,则过圆心作直线的垂线,证明圆心到直线的距离与圆的半径相等,简记为“未知圆上点,作垂直,证半径”.
口诀:已知圆上点,连半径,证垂直;
未知圆上点,作垂直,证半径。
归纳总结2:
在运用切线长定理时,要注意切线长定理与等腰三角形,勾股定理,垂径定理,切线的性质及圆中有关的性质定理等知识的联系与运用。
三三两两一直线
拓展:切线长定理的一个基本图形,包含的其他结论有:
(1)三组垂直线段:OA⊥PA,OB⊥PB,AB⊥OP;
(2)三组全等三角形:△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP;
(3)两组相等的弧: ;
(4)两个等腰三角形:△OAB,△PAB;
(5)一条特殊的直线:OP平分∠APB和∠AOB
例5.如图,AB为☉O的直径,C为☉O上的一点,AD和过
点C的切线互相垂直,垂足为D。求证:AC平分∠DAB。
变式5-1 如图,一个边长为4cm的等边△ABC的高与☉O的
直径相等, ☉O与BC相切于点C,与AC相交于点E,则
CE的长为 .
M
归纳总结:
当已知圆的切线和切点时,通常需要连接圆心和切点,可以得到
切线与半径垂直。充分运用切线的有关性质“两过一垂直”。
1.切线垂直于过切点的半径.
2.经过圆心垂直于切线的直线必过切点.
3.经过切点垂直于切线的直线必过圆心.
切线的性质:
以上关于切线的性质可归纳为:已知直线满足a.过圆心,b.过切点,c.垂直于切线中任意两个,便得到第三个结论.
两过一垂直
课堂小结
1.直线与圆的位置关系
2.切线的判定方法及其性质:
特别记忆:证切线时常用辅助线添加方法:
①已知圆上点,连半径,证垂直;
②已知圆上点,作垂直,证半径.
3.切线长定理及其简单应用。
2.如图,在△ABC中,AB=3,AC=4,BC=5,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是( )
A.相切 B.相交
C.相离 D.无法确定
复习检测(共五道题目,每题20分, 满分100分 )
1.如图:在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,则∠AOB = .
3.如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(-3,0),将☉P沿x轴的正方向平移,使得☉P与y轴相切,则平移的距离为( )
A.1 B.3 C.5 D.1或5
4.如图,已知PA、PB、EF分别切于A、B、D,若PA=15cm,则△PEF的周长是
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径.
O
知识点4:三角形的内切圆及内心的概念
名称 定义 图示
三角形的内切圆 与三角形的三边都相切的圆
三角形的内心 三角形内切圆的圆心,也是三角形内角平分线的交点 例6.(1) 如图,△ABC中,∠ B=43°,∠C=61 °,点I是
△ABC的内心,求∠ BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点I是△ABC的内心,
∴IB,IC分别是∠ B,∠C的平分线,
在△IBC中,
归纳总结:在解决三角形内切圆的相关问题时,常利用切线的性质,在直角三角形中借助方程来解决问题,或利用内心是角平分线的交点来进行角度的计算.
(2)在Rt△ABC中,AC=8,BC=6,则△ABC的
内切圆半径r = .
变式6-1 设△ABC的面积为S,周长为L, △ABC内切圆的半径为r,则S,L与r之间的数量关系是= .
变式6-2 ☉O 内切于四边形ABCD,AB=10,BC=7,
CD=8.求AD的长度。
知识拓展一:弦切角的定义及性质
1.定义:顶点在圆上,一边和圆相交,另一边和圆相切的叫弦切角。
2.弦切角定理:弦切角等于它所夹的弧所对的圆周角。
拓展应用1:如图,AB为☉O的直径,圆周角∠ ABC=40°,
当∠ BCD= °时,CD为☉O的切线。
同课章节目录
