第22章 二次函数 复习 课件 2021--2022学年人教版九年级数学上册(共31张PPT)
文档属性
| 名称 | 第22章 二次函数 复习 课件 2021--2022学年人教版九年级数学上册(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 478.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 16:36:22 | ||
图片预览






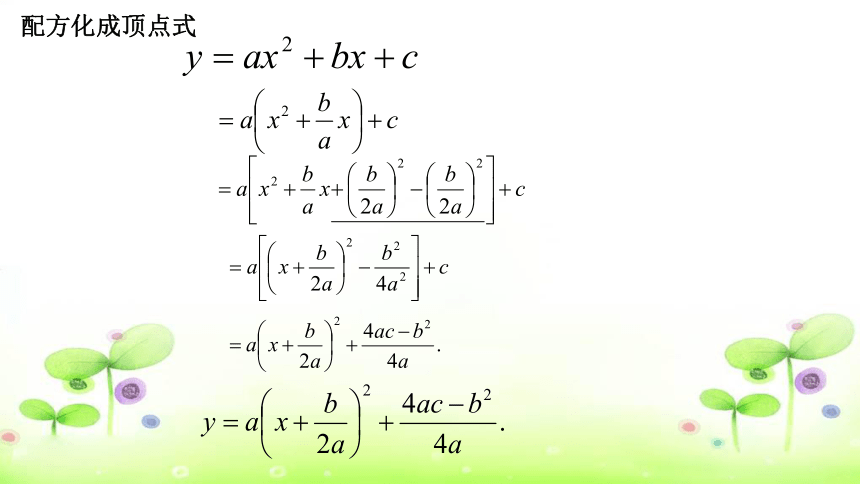

文档简介
(共31张PPT)
二次函数(1)
一般地,形如 (a,b,c是常数, __)的函数,叫做二次函数.
y=ax2+bx+c
a ≠0
1.二次函数的概念
一. 二次函数的概念及表达式
2. 二次函数解析式的三种表达式
(1)一般式:y=ax2+bx+c (a≠0)
(2)顶点式:y=a(x-h)2+k (a≠0)
(3)交点式:y=a(x-x1)(x-x2) (a≠0)
二. 二次函数的图象和性质
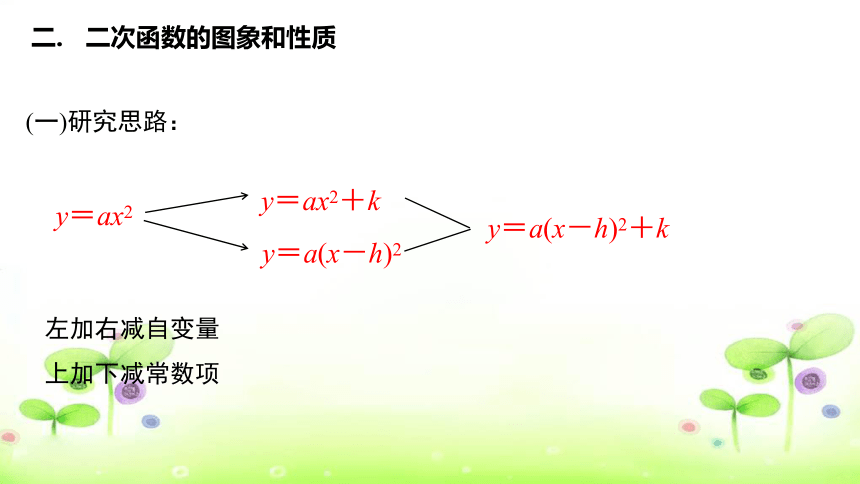
(一)研究思路:
y=ax2
y=a(x-h)2
y=ax2+k
y=a(x-h)2+k
左加右减自变量
上加下减常数项
二. 二次函数的图象和性质
y=ax2 a>0 a<0
开口方向 开口向上 开口向下
对称轴 y轴(x=0) 顶点坐标 (0,0) 增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大. 当x<0时,y随x的增大而增大;当x>0时,y随x的增大而 减小.
最值 当x=0时,y有最小值y=0 当x= 0 时,y有最大值y=0
y=a(x-h)2+k a>0 a<0
开口方向 开口向上 开口向下
对称轴 x=h 顶点坐标 (h,k) 增减性 当xh时,y随x的增大而增大. 当xh时,y随x的增大而减小.
最值 当x=h时,y有最小值y=k 当x= h 时,y有最大值y=k
配方化成顶点式
1.二次函数y=(x-1)2+3图象的顶点坐标是( )
A. (1.3) B.(1,-3) C.(-1.3) D.(-1.-3)
2.物线y=-3x2+6x+2的对称轴是( )
A.直线 x=2 B.直线x=-2 C.直线x=1 D.直线 x=-1
3.对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
4.将抛物线y=x2-6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
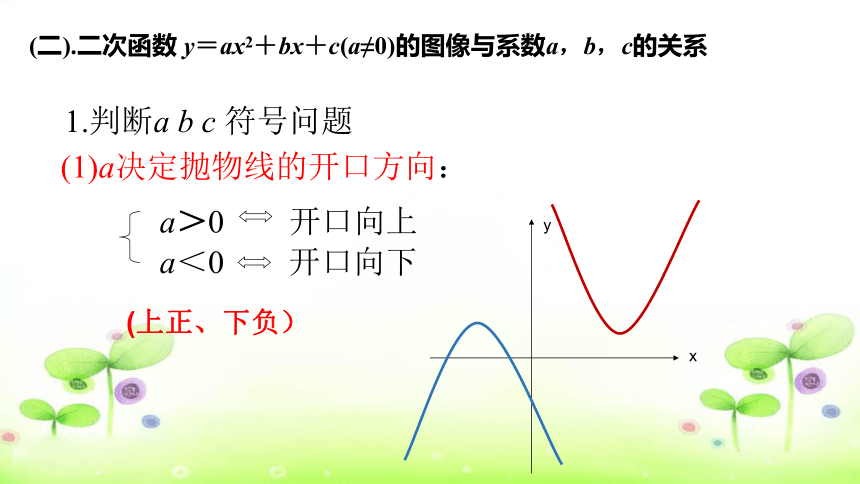
(1)a决定抛物线的开口方向:
a<0 开口向下
x
y
(上正、下负)
1.判断a b c 符号问题
a>0 开口向上
(二).二次函数 y=ax2+bx+c(a≠0)的图像与系数a,b,c的关系
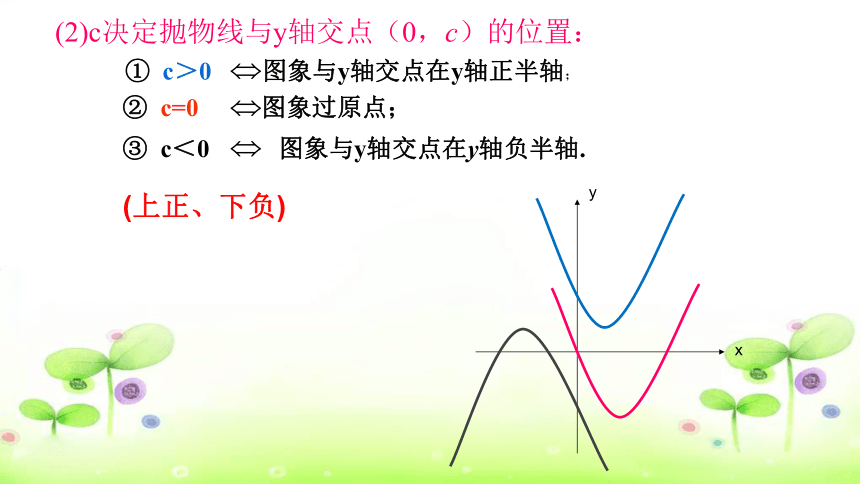
③ c<0 图象与y轴交点在y轴负半轴.
(2)c决定抛物线与y轴交点(0,c)的位置:
① c>0 图象与y轴交点在y轴正半轴;
② c=0 图象过原点;
x
y
(上正、下负)
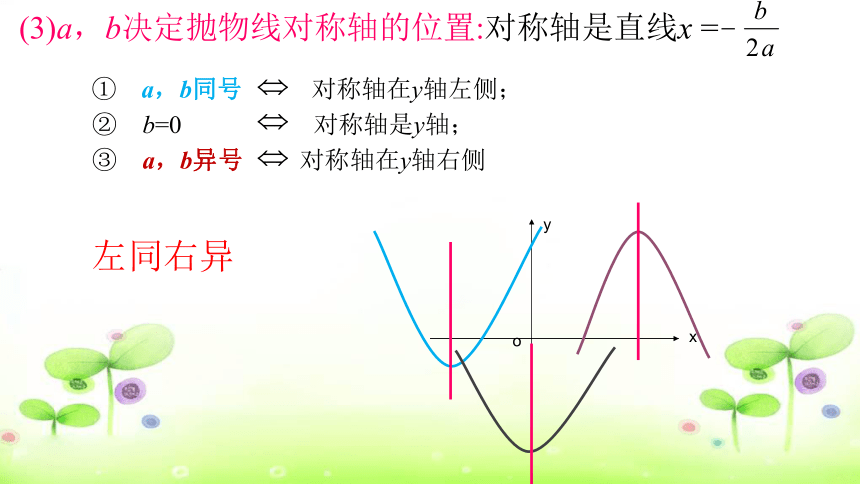
(3)a,b决定抛物线对称轴的位置:对称轴是直线x =
① a,b同号 对称轴在y轴左侧;
② b=0 对称轴是y轴;
③ a,b异号 对称轴在y轴右侧
o
x
y
左同右异
y
o
x
y
o
x
y
o
x
① △>0 抛物线与x轴有两个交点;
② △=0 抛物线与x轴有唯一的公共点;
③ △<0 抛物线与x轴无交点.
2.判断△= b2-4ac 与0的关系 抛物线与x轴交点情况:
o
x
y
3.判断 a+b+c 与0的关系 抛物线与直线x=+1交点情况
x=1
o
x
y
x= -1
3.判断 a+b+c 与0的关系 抛物线与直线x=+1交点情况
o
x
y
x= -2
判断 4a+2b+c 与0的关系 抛物线与直线x=+2交点情况
x=2
类似地
o
x
y
4.判断 2a+b 、2a-b 与0的关系 对称轴与直线x=1、x= -1
x=1
2a+b=0
o
x
y
4.判断 2a+b 、2a-b 与0的关系 对称轴与直线x=1、x= -1
x= -1
2a-b=0
已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
2a-b_____0,
b2-4ac_____0
a+b+c_____0, a-b+c___0
4a-2b+c_____0
0
-1
1
-2
针对训练
已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
2a-b_____0,
b2-4ac_____0
a+b+c____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
<
>
>
>
>
>
针对训练
o
x
y
x=1
x= -1
2a+b=0
2a-b=0
5.判断 ma+nc或mb+nc与0的关系
思想:消元
5.已知二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
(A)k <3 (B) k<3 且k ≠0 (C) k ≤3 (D) k≤3 且k ≠0
6.已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的是 ( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
7.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x -1 0 2 3 4
y 5 0 -4 -3 0
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当00;④抛物线与x轴的两个交点间的距离是4;⑤若A(x1,2),B(x2,3)是抛物线上两点,则x1A.2 B.3 C.4 D.5
8.如图,是二次函数y=ax2+bx+c图象的一部分,下列结论中:
①abc>0;②a﹣b+c<0;③ax2+bx+c+1=0有两个相等的实数根;
④﹣4a<b<﹣2a.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
9.二次函数y=ax2+bx+c的部分图象如图所示,有以下结论:①3a –b=0;②b2-4ac>0;③5a-2b+c>0; ④4b+3c>0,其中错误结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
11.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(-1,0),顶点(1,n),判断下列结论的正误:
①abc>0; ( )
②a+b+c<0 ; ( )
③a-b+c>0; ( )
④4a-2b+c<0; ( )
⑤b2 4ac>0; ( )
⑥ax2+bx+c=0两根为x1=-1,x2=3 ( )
⑦当时y>0, 1⑧ax2+bx+c+2=0有两个不相等的实数根. ( )
12.将抛物线y=ax2+bx+c向上平移1个单位,再向右平移1个单位,得到y=2x2-4x-1则a= ,b= ,c= .
13.已知抛物线y=x2-(2m-1)x-6m与x轴两交点的横坐标x1,x2,满足x1x2=x1+x2+49.问此抛物线向右平移_______单位过原点.
19.抛物线y=2x2-4x+3绕坐标原点旋转180°所得的抛物线解析式是_____________.
二次函数(1)
一般地,形如 (a,b,c是常数, __)的函数,叫做二次函数.
y=ax2+bx+c
a ≠0
1.二次函数的概念
一. 二次函数的概念及表达式
2. 二次函数解析式的三种表达式
(1)一般式:y=ax2+bx+c (a≠0)
(2)顶点式:y=a(x-h)2+k (a≠0)
(3)交点式:y=a(x-x1)(x-x2) (a≠0)
二. 二次函数的图象和性质
(一)研究思路:
y=ax2
y=a(x-h)2
y=ax2+k
y=a(x-h)2+k
左加右减自变量
上加下减常数项
二. 二次函数的图象和性质
y=ax2 a>0 a<0
开口方向 开口向上 开口向下
对称轴 y轴(x=0) 顶点坐标 (0,0) 增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大. 当x<0时,y随x的增大而增大;当x>0时,y随x的增大而 减小.
最值 当x=0时,y有最小值y=0 当x= 0 时,y有最大值y=0
y=a(x-h)2+k a>0 a<0
开口方向 开口向上 开口向下
对称轴 x=h 顶点坐标 (h,k) 增减性 当x
最值 当x=h时,y有最小值y=k 当x= h 时,y有最大值y=k
配方化成顶点式
1.二次函数y=(x-1)2+3图象的顶点坐标是( )
A. (1.3) B.(1,-3) C.(-1.3) D.(-1.-3)
2.物线y=-3x2+6x+2的对称轴是( )
A.直线 x=2 B.直线x=-2 C.直线x=1 D.直线 x=-1
3.对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
4.将抛物线y=x2-6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
(1)a决定抛物线的开口方向:
a<0 开口向下
x
y
(上正、下负)
1.判断a b c 符号问题
a>0 开口向上
(二).二次函数 y=ax2+bx+c(a≠0)的图像与系数a,b,c的关系
③ c<0 图象与y轴交点在y轴负半轴.
(2)c决定抛物线与y轴交点(0,c)的位置:
① c>0 图象与y轴交点在y轴正半轴;
② c=0 图象过原点;
x
y
(上正、下负)
(3)a,b决定抛物线对称轴的位置:对称轴是直线x =
① a,b同号 对称轴在y轴左侧;
② b=0 对称轴是y轴;
③ a,b异号 对称轴在y轴右侧
o
x
y
左同右异
y
o
x
y
o
x
y
o
x
① △>0 抛物线与x轴有两个交点;
② △=0 抛物线与x轴有唯一的公共点;
③ △<0 抛物线与x轴无交点.
2.判断△= b2-4ac 与0的关系 抛物线与x轴交点情况:
o
x
y
3.判断 a+b+c 与0的关系 抛物线与直线x=+1交点情况
x=1
o
x
y
x= -1
3.判断 a+b+c 与0的关系 抛物线与直线x=+1交点情况
o
x
y
x= -2
判断 4a+2b+c 与0的关系 抛物线与直线x=+2交点情况
x=2
类似地
o
x
y
4.判断 2a+b 、2a-b 与0的关系 对称轴与直线x=1、x= -1
x=1
2a+b=0
o
x
y
4.判断 2a+b 、2a-b 与0的关系 对称轴与直线x=1、x= -1
x= -1
2a-b=0
已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
2a-b_____0,
b2-4ac_____0
a+b+c_____0, a-b+c___0
4a-2b+c_____0
0
-1
1
-2
针对训练
已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
2a-b_____0,
b2-4ac_____0
a+b+c____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
<
>
>
>
>
>
针对训练
o
x
y
x=1
x= -1
2a+b=0
2a-b=0
5.判断 ma+nc或mb+nc与0的关系
思想:消元
5.已知二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
(A)k <3 (B) k<3 且k ≠0 (C) k ≤3 (D) k≤3 且k ≠0
6.已知二次函数y=x2-4x+2,关于该函数在-1≤x≤3的取值范围内,下列说法正确的是 ( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
7.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x -1 0 2 3 4
y 5 0 -4 -3 0
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0
8.如图,是二次函数y=ax2+bx+c图象的一部分,下列结论中:
①abc>0;②a﹣b+c<0;③ax2+bx+c+1=0有两个相等的实数根;
④﹣4a<b<﹣2a.其中正确结论的序号为( )
A.①② B.①③ C.②③ D.①④
9.二次函数y=ax2+bx+c的部分图象如图所示,有以下结论:①3a –b=0;②b2-4ac>0;③5a-2b+c>0; ④4b+3c>0,其中错误结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
11.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(-1,0),顶点(1,n),判断下列结论的正误:
①abc>0; ( )
②a+b+c<0 ; ( )
③a-b+c>0; ( )
④4a-2b+c<0; ( )
⑤b2 4ac>0; ( )
⑥ax2+bx+c=0两根为x1=-1,x2=3 ( )
⑦当时y>0, 1
12.将抛物线y=ax2+bx+c向上平移1个单位,再向右平移1个单位,得到y=2x2-4x-1则a= ,b= ,c= .
13.已知抛物线y=x2-(2m-1)x-6m与x轴两交点的横坐标x1,x2,满足x1x2=x1+x2+49.问此抛物线向右平移_______单位过原点.
19.抛物线y=2x2-4x+3绕坐标原点旋转180°所得的抛物线解析式是_____________.
同课章节目录
