2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.1.2椭圆的简单几何性质 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.1.2椭圆的简单几何性质 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 12:44:44 | ||
图片预览






文档简介
(共27张PPT)
3.1.2
椭圆的简单几何性质
高二数学选择性必修第一册 第三章 圆锥曲线的方程
学习目标
1.掌握椭圆的几何图形及简单几何性质;
2.能用坐标法解决一些与椭圆有关的简单几何问题和实际问题;
3.通过学习椭圆,进一步体会数形结合的思想.
4.核心素养:数学抽象、逻辑推理。
1.椭圆的定义:
平面内与两个定点F1、F2的距离之和为常数2a (大于|F1F2 |)的动点M的轨迹叫做椭圆.
2.椭圆的标准方程:
3.椭圆中a,b,c的关系:
当焦点在X轴上时
当焦点在Y轴上时
a2=b2+c2
一、回顾旧知:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线x=±a,y= ± b所围成的矩形中,
如图所示:
o
y
B2
B1
A1
A2
F1
F2
c
a
b
1.椭圆 的范围:
由
x
二、探究新知
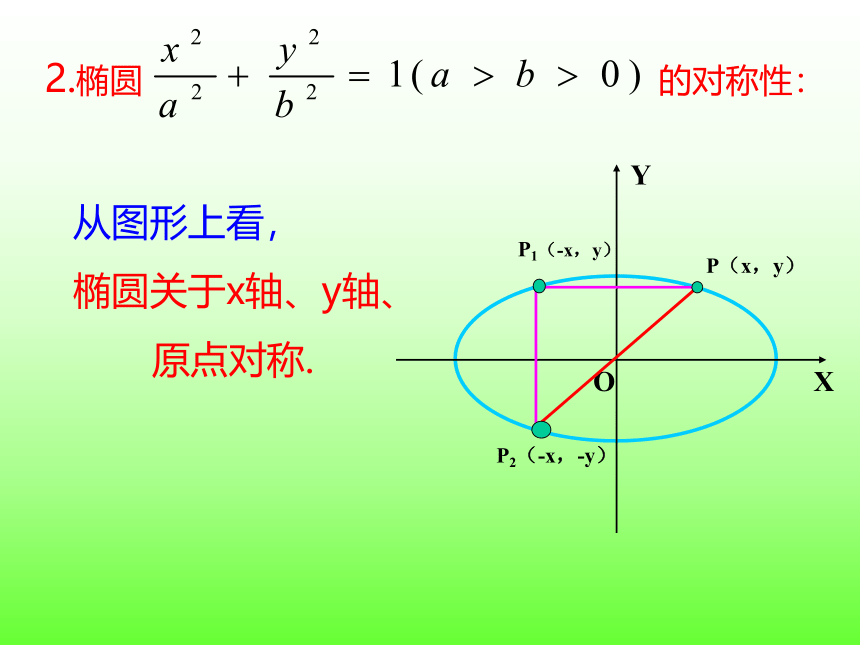
2.椭圆 的对称性:
从图形上看,
椭圆关于x轴、y轴、
原点对称.
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
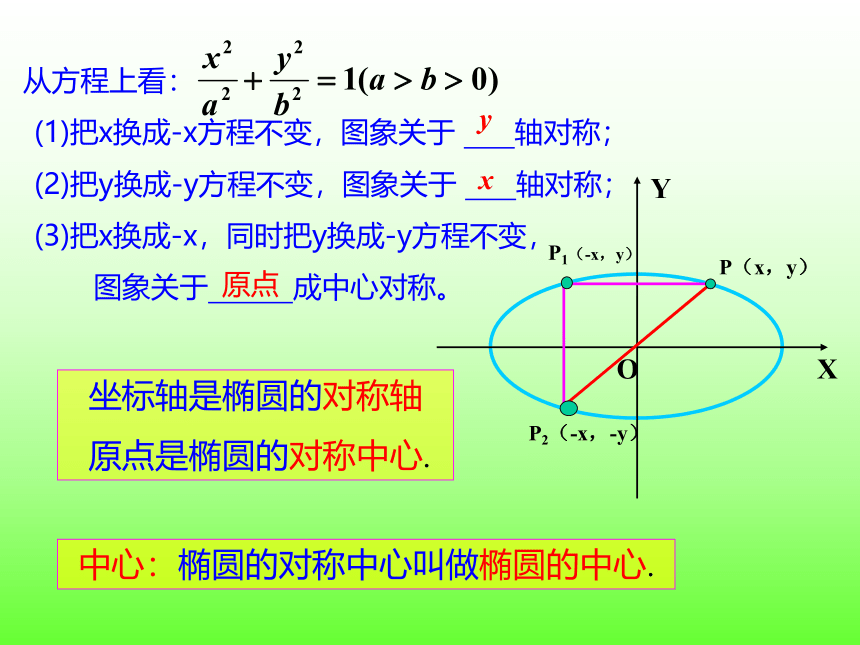
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心.
中心:椭圆的对称中心叫做椭圆的中心.
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
*长轴、短轴:
线段A1A2、B1B2分别
叫做椭圆的长轴和短轴。
它们的长分别等于2 a和2 b 。
a、b分别叫做椭圆的长半轴长和短半轴长.
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(0,-b)
(a,0)
(-a,0)
3. 椭圆 的顶点:
令 x=0,得 y=?说明椭圆与 y轴的交点为( ),
令 y=0,得 x=?说明椭圆与 x轴的交点为( )。
0, ±b
±a, 0
*顶点:椭圆与它的对称轴的四个
交点,叫做椭圆的顶点。
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
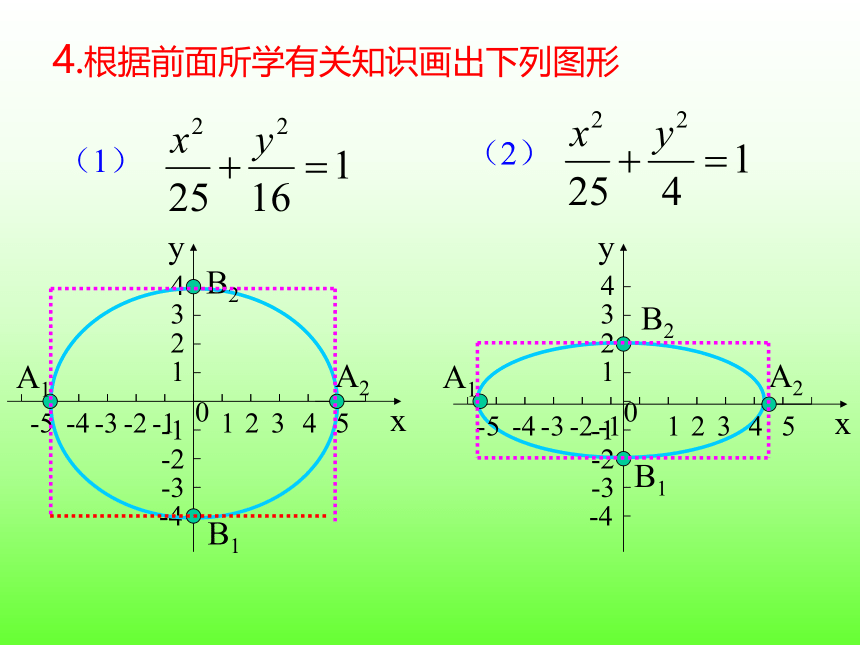
4.根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
0
0
5.椭圆的离心率
离心率:椭圆的焦距与长轴长的比
叫做椭圆的离心率.
(1)离心率的取值范围:
(2)离心率对椭圆形状的影响:
0①e 越接近 1,c 就越接近 a,请问:此时椭圆的变化情况?
(3)e与a,b的关系:
用e表示,即
思考:当e=0时,曲线是什么?当e=1时曲线又是什么?
②e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?
e 越接近 1,c 就越接近 a, b就越小,此时椭圆就越扁
e 越接近 0,c 就越接近 0, b就越大,此时椭圆就越圆
(e用来刻画椭圆扁平程度的量)
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
(1)基本量:a、b、c、e、(共四个量)
(2)基本点:顶点、焦点、中心(共七个点)
(3)基本线:对称轴(共两条线)
思考:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)
6.椭圆的基本元素
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
-a ≤ x≤ a, - b≤ y≤ b
关于x轴、y轴成轴对称;
关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. (a>b)
a2=b2+c2
7.椭圆的几何性质
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的
关系
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,
短半轴长为b. (a>b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,
短半轴长为b.(a>b)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a, - b≤ x ≤ b
a2=b2+c2
a2=b2+c2
1.练习:已知椭圆方程为16x2+25y2=400,则
它的长轴长是: ;短轴长是: ;
焦距是: ;离心率等于: ;
焦点坐标是: ;顶点坐标是: ;
外切矩形的面积等于: ;
10
8
6
80
解题步骤:
1、将椭圆方程转化为标准方程求a、b:
2、确定焦点的位置和长轴的位置.
三、巩固新知:
2.变式:求适合下列条件的椭圆的标准方程
(1) a=6, e= , 焦点在x轴上.
(2) 离心率 e=0.8, 焦距为8.
(3) 长轴是短轴的2倍, 且过点P(2,-6).
求椭圆的标准方程时, 应: 先定位(焦点), 再定量[a、b ]
当焦点位置不确定时,要讨论,此时有两个解!
(4)在x轴上的一个焦点与短轴两端点的连线互相垂直,
且焦距为6.
3.例5.
4.例6.
O
x
y
M
F
d
H
解:
思考上面探究问题,并回答下列问题:
5.探究:
(1)用坐标法如何求出其轨迹方程,并说出轨迹
(2)给椭圆下一个新的定义
O
x
y
M
F
d
H
O
x
y
M
F
d
H
6.椭圆第二定义:
注意:我们一般把这个定义称为椭圆的第二定义,
而相应的把另一个定义称为椭圆的第一定义.
定点是椭圆的焦点,定直线叫做椭圆的准线.
7.椭圆的第一定义与第二定义是相呼应的
定义 1 图 形 定义 2
平面内与
8.椭圆与直线的位置关系及判断方法
(1)联立方程组
(2)消去一个未知数
相离
相切
相交
<0
=0
>0
判断方法
9.例7.
F1
F2
O
x
y
⑴-25<m <25,有两个交点; ⑵m1=-25, m2= 25,有一个交点; ⑶ m < -25或m >25,没有交点.
10.变式:
F1
F2
x
O
y
11.变式:
F1
F2
O
x
y
解:
12变式:
O
x
y
P
F1
F2
解:
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. (a>b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a,- b≤ x ≤ b
a2=b2+c2
四.课堂小结
作业: 课本P115 习题3.1 4 题
3.1.2
椭圆的简单几何性质
高二数学选择性必修第一册 第三章 圆锥曲线的方程
学习目标
1.掌握椭圆的几何图形及简单几何性质;
2.能用坐标法解决一些与椭圆有关的简单几何问题和实际问题;
3.通过学习椭圆,进一步体会数形结合的思想.
4.核心素养:数学抽象、逻辑推理。
1.椭圆的定义:
平面内与两个定点F1、F2的距离之和为常数2a (大于|F1F2 |)的动点M的轨迹叫做椭圆.
2.椭圆的标准方程:
3.椭圆中a,b,c的关系:
当焦点在X轴上时
当焦点在Y轴上时
a2=b2+c2
一、回顾旧知:
-a≤x≤a, -b≤y≤b
∴椭圆位于直线x=±a,y= ± b所围成的矩形中,
如图所示:
o
y
B2
B1
A1
A2
F1
F2
c
a
b
1.椭圆 的范围:
由
x
二、探究新知
2.椭圆 的对称性:
从图形上看,
椭圆关于x轴、y轴、
原点对称.
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴
原点是椭圆的对称中心.
中心:椭圆的对称中心叫做椭圆的中心.
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
*长轴、短轴:
线段A1A2、B1B2分别
叫做椭圆的长轴和短轴。
它们的长分别等于2 a和2 b 。
a、b分别叫做椭圆的长半轴长和短半轴长.
o
y
B2
B1
A1
A2
F1
F2
c
a
b
(0,b)
(0,-b)
(a,0)
(-a,0)
3. 椭圆 的顶点:
令 x=0,得 y=?说明椭圆与 y轴的交点为( ),
令 y=0,得 x=?说明椭圆与 x轴的交点为( )。
0, ±b
±a, 0
*顶点:椭圆与它的对称轴的四个
交点,叫做椭圆的顶点。
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
4.根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
0
0
5.椭圆的离心率
离心率:椭圆的焦距与长轴长的比
叫做椭圆的离心率.
(1)离心率的取值范围:
(2)离心率对椭圆形状的影响:
0
(3)e与a,b的关系:
用e表示,即
思考:当e=0时,曲线是什么?当e=1时曲线又是什么?
②e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?
e 越接近 1,c 就越接近 a, b就越小,此时椭圆就越扁
e 越接近 0,c 就越接近 0, b就越大,此时椭圆就越圆
(e用来刻画椭圆扁平程度的量)
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
(1)基本量:a、b、c、e、(共四个量)
(2)基本点:顶点、焦点、中心(共七个点)
(3)基本线:对称轴(共两条线)
思考:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)
6.椭圆的基本元素
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
-a ≤ x≤ a, - b≤ y≤ b
关于x轴、y轴成轴对称;
关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. (a>b)
a2=b2+c2
7.椭圆的几何性质
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的
关系
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,
短半轴长为b. (a>b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,
短半轴长为b.(a>b)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a, - b≤ x ≤ b
a2=b2+c2
a2=b2+c2
1.练习:已知椭圆方程为16x2+25y2=400,则
它的长轴长是: ;短轴长是: ;
焦距是: ;离心率等于: ;
焦点坐标是: ;顶点坐标是: ;
外切矩形的面积等于: ;
10
8
6
80
解题步骤:
1、将椭圆方程转化为标准方程求a、b:
2、确定焦点的位置和长轴的位置.
三、巩固新知:
2.变式:求适合下列条件的椭圆的标准方程
(1) a=6, e= , 焦点在x轴上.
(2) 离心率 e=0.8, 焦距为8.
(3) 长轴是短轴的2倍, 且过点P(2,-6).
求椭圆的标准方程时, 应: 先定位(焦点), 再定量[a、b ]
当焦点位置不确定时,要讨论,此时有两个解!
(4)在x轴上的一个焦点与短轴两端点的连线互相垂直,
且焦距为6.
3.例5.
4.例6.
O
x
y
M
F
d
H
解:
思考上面探究问题,并回答下列问题:
5.探究:
(1)用坐标法如何求出其轨迹方程,并说出轨迹
(2)给椭圆下一个新的定义
O
x
y
M
F
d
H
O
x
y
M
F
d
H
6.椭圆第二定义:
注意:我们一般把这个定义称为椭圆的第二定义,
而相应的把另一个定义称为椭圆的第一定义.
定点是椭圆的焦点,定直线叫做椭圆的准线.
7.椭圆的第一定义与第二定义是相呼应的
定义 1 图 形 定义 2
平面内与
8.椭圆与直线的位置关系及判断方法
(1)联立方程组
(2)消去一个未知数
相离
相切
相交
<0
=0
>0
判断方法
9.例7.
F1
F2
O
x
y
⑴-25<m <25,有两个交点; ⑵m1=-25, m2= 25,有一个交点; ⑶ m < -25或m >25,没有交点.
10.变式:
F1
F2
x
O
y
11.变式:
F1
F2
O
x
y
解:
12变式:
O
x
y
P
F1
F2
解:
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. (a>b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
-a ≤ x≤ a, - b≤ y≤ b
-a ≤ y ≤ a,- b≤ x ≤ b
a2=b2+c2
四.课堂小结
作业: 课本P115 习题3.1 4 题
