人教高中数学选修2-3第二章2.2.3-独立重复试验与二项分布 课件(22张ppt)
文档属性
| 名称 | 人教高中数学选修2-3第二章2.2.3-独立重复试验与二项分布 课件(22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 680.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
2.2.3 独立重复试验与二项分布
复习引入
引例
基本概念
①包含了n个相同的试验; ②每次试验相互独立;
③每次试验只有两种可能的结果:“成功”或“失败”;
④每次出现“成功”的概率相同为p ,“失败“的概率也相同,为1-p;
⑤试验”成功”或“失败”可以计数,即试验结果对应于一个离散型随机变量。
独立重复试验的特点:
等价于各次试验的结果不会受其他试验的影响
判断下列试验是不是独立重复试验:
1).依次投掷四枚质地不同的硬币,3次正面向上;
2).某射击手每次击中目标的概率是0.9,他进行了4
次射击,只命中一次;
3).口袋装有5个白球,3个红球,2个黑球,从中依次
抽取5个球,恰好抽出4个白球;
4).口袋装有5个白球,3个红球,2个黑球,从中有放回
的抽取5个球,恰好抽出4个白球
不是
是
不是
是
注:独立重复试验的实际原型是有放回的抽样试验
探究
投掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率为q=1-p.连续掷一枚图钉3次,仅出现1次针尖向上的概率是多少?
连续掷一枚图钉3次,就是做3次独立重复试验。用 表示第i次掷得针尖向上的事件,用 表示“仅出现一次针尖向上”的事件,则
由于事件 彼此互斥,由概率加法公式得
所以,连续掷一枚图钉3次,仅出现1次针尖向上的概率是
思考?
上面我们利用掷1次图钉,针尖向上的概率为p,求出了连续掷3次图钉,仅出现次1针尖向上的概率。类似地,连续掷3次图钉,出现 次针尖向上的概率是多少?你能发现其中的规律吗?
仔细观察上述等式,可以发现
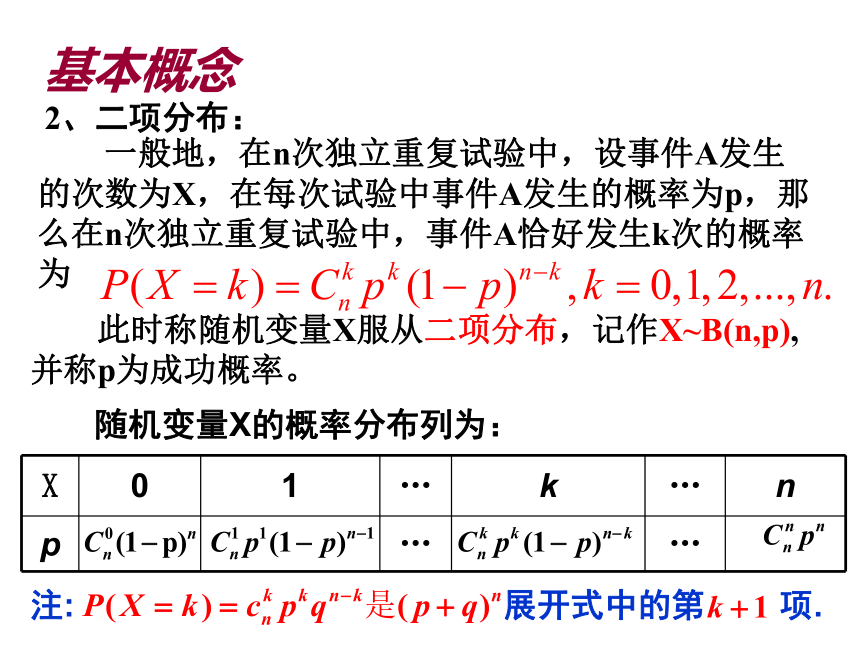
基本概念
2、二项分布:
一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。
注: 展开式中的第 项.
X 0 1 … k … n
p … …
随机变量X的概率分布列为:
(其中k = 0,1,2,···,n )
试验总次数
事件 A 发生的次数
一次试验中事件 A 发生的概率
公式理解
例1某射手每次射击击中目标的概率是0.8 , 求这名射
手在10次射击中 ,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率 .
例2、某所气象预报站的预报准确率为80%,试计算(保留两位有效数字):
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率。
解:
这个问题为一个5次独立重复试验,其中“预报1次,结果准确”为事件A,p=0.8, 1-p=0.2。
(1)5次预报中4次准确的概率为:
(2)5次预报中至少有4次准确的概率为:
例3: 某城市的发电厂有5台发电机组,每台机组在一个季度里停机维修率为1/4,已知3台以上机组停机维修,将造成城市缺电。计算:
①该城市在一个季度里停电的概率;
②该城市在一个季度里缺电的概率。
①解:该城市停电必须是5台机组都停电维修,所以停电的概率是
②解:当3台或4台或5台机组停电维修时,该城市将缺电,所以缺电的概率是
练习
已知一个射手每次击中目标的概率为 ,求他在3次射击中下列事件发生的概率。
(1)命中一次;
(2)恰在第三次命中目标;
(3)命中两次;
(4)刚好在第二、第三两次击中目标。
1、每次试验的成功率为
重复进行10次试验,其中前
7次都未成功后3次都成功的概率为( )
2、已知随机变量
服从二项分布,
3、甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为
3:2,比赛时均能正常发挥技术水平,则在5局3胜制中,甲
打完4局才胜的概率为( )
C
D
A
课堂练习
课堂练习
4.某机器正常工作的概率是 ,5天内有4天正常工作的概率是( )
5.在4次独立重复试验中,若已知事件A至少发生一次的概率是
则事件A在一次试验中发生的概率是
课堂练习
6、 在某一试验中, A出现的概率为P,则在n次试验中 出现k次的概率为
7、100件产品中有3件不合格,有放回地连续抽取10次,每次一件,10件产品中恰有2件不合格的概率为
8、某人投篮的命中率为2/3,他连续投5次,则至多投中4次的概率为
例4.设3次独立重复试验中,事件A发生的概率相等,若已知A至少发生一次的概率等于19/27,求事件A在一次试验中发生的概率。
独立重复试验
二项分布
课堂小结
2.2.3 独立重复试验与二项分布
复习引入
引例
基本概念
①包含了n个相同的试验; ②每次试验相互独立;
③每次试验只有两种可能的结果:“成功”或“失败”;
④每次出现“成功”的概率相同为p ,“失败“的概率也相同,为1-p;
⑤试验”成功”或“失败”可以计数,即试验结果对应于一个离散型随机变量。
独立重复试验的特点:
等价于各次试验的结果不会受其他试验的影响
判断下列试验是不是独立重复试验:
1).依次投掷四枚质地不同的硬币,3次正面向上;
2).某射击手每次击中目标的概率是0.9,他进行了4
次射击,只命中一次;
3).口袋装有5个白球,3个红球,2个黑球,从中依次
抽取5个球,恰好抽出4个白球;
4).口袋装有5个白球,3个红球,2个黑球,从中有放回
的抽取5个球,恰好抽出4个白球
不是
是
不是
是
注:独立重复试验的实际原型是有放回的抽样试验
探究
投掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率为q=1-p.连续掷一枚图钉3次,仅出现1次针尖向上的概率是多少?
连续掷一枚图钉3次,就是做3次独立重复试验。用 表示第i次掷得针尖向上的事件,用 表示“仅出现一次针尖向上”的事件,则
由于事件 彼此互斥,由概率加法公式得
所以,连续掷一枚图钉3次,仅出现1次针尖向上的概率是
思考?
上面我们利用掷1次图钉,针尖向上的概率为p,求出了连续掷3次图钉,仅出现次1针尖向上的概率。类似地,连续掷3次图钉,出现 次针尖向上的概率是多少?你能发现其中的规律吗?
仔细观察上述等式,可以发现
基本概念
2、二项分布:
一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。
注: 展开式中的第 项.
X 0 1 … k … n
p … …
随机变量X的概率分布列为:
(其中k = 0,1,2,···,n )
试验总次数
事件 A 发生的次数
一次试验中事件 A 发生的概率
公式理解
例1某射手每次射击击中目标的概率是0.8 , 求这名射
手在10次射击中 ,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率 .
例2、某所气象预报站的预报准确率为80%,试计算(保留两位有效数字):
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率。
解:
这个问题为一个5次独立重复试验,其中“预报1次,结果准确”为事件A,p=0.8, 1-p=0.2。
(1)5次预报中4次准确的概率为:
(2)5次预报中至少有4次准确的概率为:
例3: 某城市的发电厂有5台发电机组,每台机组在一个季度里停机维修率为1/4,已知3台以上机组停机维修,将造成城市缺电。计算:
①该城市在一个季度里停电的概率;
②该城市在一个季度里缺电的概率。
①解:该城市停电必须是5台机组都停电维修,所以停电的概率是
②解:当3台或4台或5台机组停电维修时,该城市将缺电,所以缺电的概率是
练习
已知一个射手每次击中目标的概率为 ,求他在3次射击中下列事件发生的概率。
(1)命中一次;
(2)恰在第三次命中目标;
(3)命中两次;
(4)刚好在第二、第三两次击中目标。
1、每次试验的成功率为
重复进行10次试验,其中前
7次都未成功后3次都成功的概率为( )
2、已知随机变量
服从二项分布,
3、甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为
3:2,比赛时均能正常发挥技术水平,则在5局3胜制中,甲
打完4局才胜的概率为( )
C
D
A
课堂练习
课堂练习
4.某机器正常工作的概率是 ,5天内有4天正常工作的概率是( )
5.在4次独立重复试验中,若已知事件A至少发生一次的概率是
则事件A在一次试验中发生的概率是
课堂练习
6、 在某一试验中, A出现的概率为P,则在n次试验中 出现k次的概率为
7、100件产品中有3件不合格,有放回地连续抽取10次,每次一件,10件产品中恰有2件不合格的概率为
8、某人投篮的命中率为2/3,他连续投5次,则至多投中4次的概率为
例4.设3次独立重复试验中,事件A发生的概率相等,若已知A至少发生一次的概率等于19/27,求事件A在一次试验中发生的概率。
独立重复试验
二项分布
课堂小结
