5.5.1 两角和与差的正弦、余弦和正切公式第四课时 二倍角的正弦、余弦、正切公式-学案(Word版)
文档属性
| 名称 | 5.5.1 两角和与差的正弦、余弦和正切公式第四课时 二倍角的正弦、余弦、正切公式-学案(Word版) |

|
|
| 格式 | docx | ||
| 文件大小 | 64.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 12:50:44 | ||
图片预览



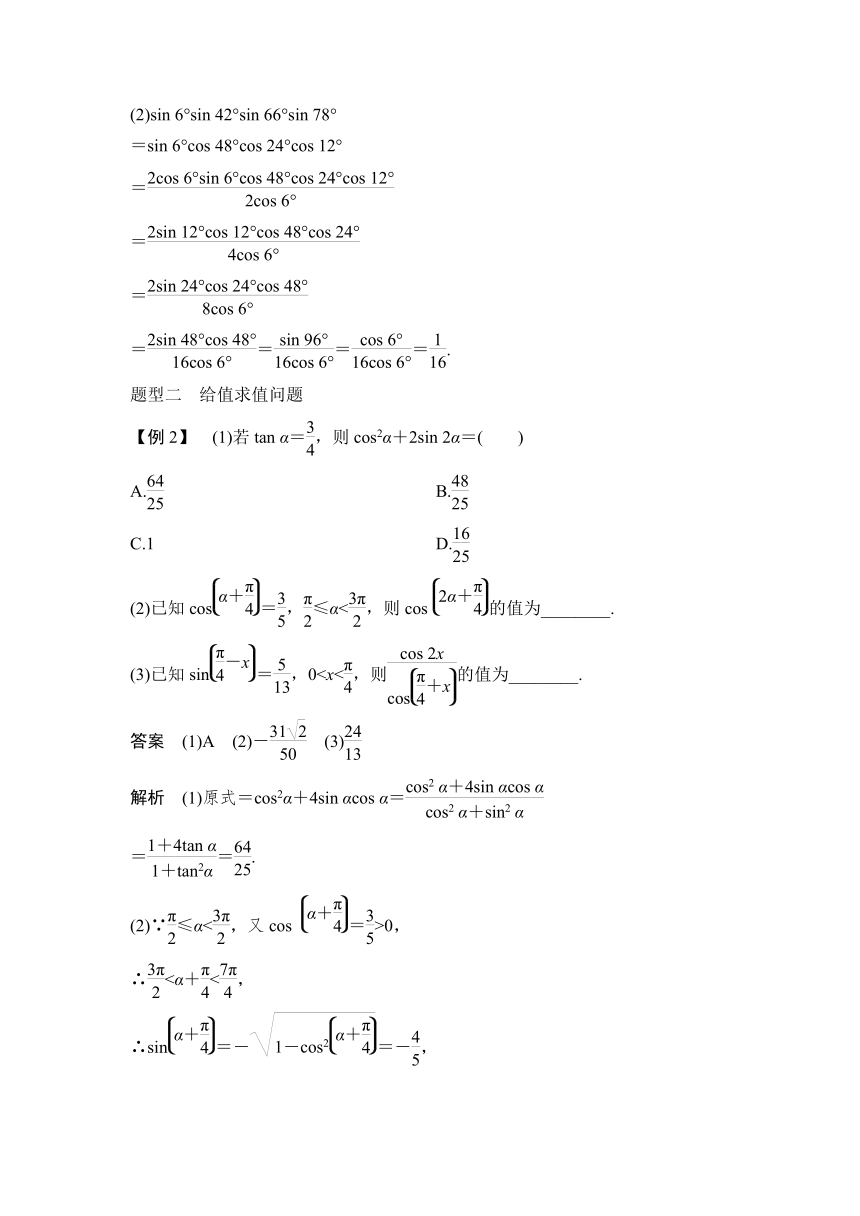
文档简介
第四课时 二倍角的正弦、余弦、正切公式-学案
课标要求 素养要求
1.会从两角和与差的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式. 2.能熟练运用二倍角的公式进行简单的恒等变换,并能灵活地将公式变形应用. 在二倍角公式的推导中,经历由特殊到一般的逻辑推理过程,发展学生的数学运算素养.
自主梳理
二倍角的正弦、余弦、正切公式
三角函数 公式 简记
正弦 sin 2α=2sin__αcos__α S2α
余弦 cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α C2α
正切 tan 2α= T2α
以上这些公式都叫做倍角公式,倍角公式给出了α的三角函数与2α的三角函数之间的关系.
(1)二倍角是相对的,如4α是2α的二倍,α是的二倍,2α+是α+的二倍等.
(2)二倍角的余弦公式的变形:
①cos2α=;
②sin2α=.
自主检验
1.思考辨析,判断正误
(1)sin α=2sincos.(√)
(2)cos2α=(1+cos 2α),cos 3α=1-2sin2α.(√)
(3)=tan.(×)
提示 公式中所含各角都要使三角函数有意义,而tan无意义.
(4)sin2-cos2=.(×)
提示 sin2-cos2=-
=-cos=-.
2.sincos的值为________.
答案
解析 sincos=sin=.
3.cos2-sin2的值为________.
答案
解析 cos2-sin2=cos=.
4.=________.
答案
解析 =tan 30°=.
题型一 给角求值问题
【例1】 求下列各式的值.
(1)1-2sin2750°;
(2);
(3)cos 20°·cos 40°·cos 80°.
解 (1)原式=cos(2×750°)=cos 1 500°=cos(4×360°+60°)=cos 60°=.
(2)原式====2.
(3)原式=2sin 20°cos 20°cos 40°cos 80°
=·sin 40°cos 40°cos 80°
=sin 80°cos 80°=·sin 160°
==.
思维升华 二倍角公式的关注点
(1)对“二倍角”应该有广义的理解,如:4α是2α的二倍角,α是的二倍角,3α是的二倍角等.
(2)公式逆用:主要形式有2sin αcos α=sin 2α,sin αcos α=sin 2α,cos α=,cos2α-sin2α=cos 2α,=tan 2α.
(3)化简求值关注四个方向:分别从“角”“函数名”“幂”“形”着手分析,消除差异.
【训练1】 (1)-cos2=________;
(2)sin 6°sin 42°sin 66°sin 78°=________.
答案 (1)- (2)
解析 (1)原式==-cos=-.
(2)sin 6°sin 42°sin 66°sin 78°
=sin 6°cos 48°cos 24°cos 12°
=
=
=
====.
题型二 给值求值问题
【例2】 (1)若tan α=,则cos2α+2sin 2α=( )
A. B.
C.1 D.
(2)已知cos=,≤α<,则cos的值为________.
(3)已知sin=,0答案 (1)A (2)- (3)
解析 (1)原式=cos2α+4sin αcos α=
==.
(2)∵≤α<,又cos =>0,
∴<α+<,
∴sin=-=-,
从而cos 2α=sin=2sincos
=-,
sin 2α=-cos=1-2cos2=.
∴cos=cos 2αcos-sin 2αsin=(cos 2α-sin 2α)=×=-.
(3)∵0∴-x∈,cos=,
利用诱导公式,sin=cos
=cos=.
∴原式==
=2sin=.
思维升华 解决给值求值问题的方法
(1)有方向地将已知式或未知式化简,使关系明朗化;寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
(2)当遇到±x这样的角时可利用互余角的关系和诱导公式,将条件与结论沟通.
【训练2】 设α为锐角,若cos=,则sin的值为________.
答案
解析 ∵α为锐角,∴<α+<.
∵cos=,∴sin=,
∴sin=sin
=2sincos
=2××=,
cos=cos
=2cos2-1
=2×-1=,
∴sin=sin
=sincos-cossin
=×=×=.
题型三 三角函数式的化简与证明
角度1 三角恒等式的证明问题
【例3-1】 求证:=tan4 A.
证明 ∵左边=
===(tan2A)2
=tan4 A=右边,
∴=tan4 A.
角度2 三角函数式的化简问题
【例3-2】 化简:.
解
=
=·
=sin x·=tan x.
思维升华 探究三角函数式化简、证明的常用技巧
(1)特殊角的三角函数与特殊值的互化;
(2)对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分;
(3)对于二次根式,注意倍角公式的逆用;
(4)利用角与角之间的隐含关系,如互余、互补等;
(5)利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
【训练3】 (1)求证:=.
(2)化简·.
(1)证明 原式变形为1+sin 4θ-cos 4θ
=tan 2θ(1+sin 4θ+cos 4θ),(*)
而(*)式右边=tan 2θ(1+cos 4θ+sin 4θ)
=(2cos22θ+2sin 2θcos 2θ)
=2sin 2θcos 2θ+2sin22θ
=sin 4θ+1-cos 4θ
=左边,
∴(*)式成立,即原式得证.
(2)解 原式=·
=·
=·=2.
1.倍角公式中的“倍角”是相对的,对于两个角的比值等于2的情况都成立,如6α是3α的2倍,3α是的2倍……这里蕴含着换元思想.这就是说,“倍”是相对而言的,是描述两个数量之间的关系的.
2.在二倍角公式中,二倍角的余弦公式最为灵活多样,应用广泛,二倍角的常用形式:①1+cos 2α=2cos2α,②cos2α=,③1-cos 2α=2sin2α,④sin2α=.
课标要求 素养要求
1.会从两角和与差的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式. 2.能熟练运用二倍角的公式进行简单的恒等变换,并能灵活地将公式变形应用. 在二倍角公式的推导中,经历由特殊到一般的逻辑推理过程,发展学生的数学运算素养.
自主梳理
二倍角的正弦、余弦、正切公式
三角函数 公式 简记
正弦 sin 2α=2sin__αcos__α S2α
余弦 cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α C2α
正切 tan 2α= T2α
以上这些公式都叫做倍角公式,倍角公式给出了α的三角函数与2α的三角函数之间的关系.
(1)二倍角是相对的,如4α是2α的二倍,α是的二倍,2α+是α+的二倍等.
(2)二倍角的余弦公式的变形:
①cos2α=;
②sin2α=.
自主检验
1.思考辨析,判断正误
(1)sin α=2sincos.(√)
(2)cos2α=(1+cos 2α),cos 3α=1-2sin2α.(√)
(3)=tan.(×)
提示 公式中所含各角都要使三角函数有意义,而tan无意义.
(4)sin2-cos2=.(×)
提示 sin2-cos2=-
=-cos=-.
2.sincos的值为________.
答案
解析 sincos=sin=.
3.cos2-sin2的值为________.
答案
解析 cos2-sin2=cos=.
4.=________.
答案
解析 =tan 30°=.
题型一 给角求值问题
【例1】 求下列各式的值.
(1)1-2sin2750°;
(2);
(3)cos 20°·cos 40°·cos 80°.
解 (1)原式=cos(2×750°)=cos 1 500°=cos(4×360°+60°)=cos 60°=.
(2)原式====2.
(3)原式=2sin 20°cos 20°cos 40°cos 80°
=·sin 40°cos 40°cos 80°
=sin 80°cos 80°=·sin 160°
==.
思维升华 二倍角公式的关注点
(1)对“二倍角”应该有广义的理解,如:4α是2α的二倍角,α是的二倍角,3α是的二倍角等.
(2)公式逆用:主要形式有2sin αcos α=sin 2α,sin αcos α=sin 2α,cos α=,cos2α-sin2α=cos 2α,=tan 2α.
(3)化简求值关注四个方向:分别从“角”“函数名”“幂”“形”着手分析,消除差异.
【训练1】 (1)-cos2=________;
(2)sin 6°sin 42°sin 66°sin 78°=________.
答案 (1)- (2)
解析 (1)原式==-cos=-.
(2)sin 6°sin 42°sin 66°sin 78°
=sin 6°cos 48°cos 24°cos 12°
=
=
=
====.
题型二 给值求值问题
【例2】 (1)若tan α=,则cos2α+2sin 2α=( )
A. B.
C.1 D.
(2)已知cos=,≤α<,则cos的值为________.
(3)已知sin=,0
解析 (1)原式=cos2α+4sin αcos α=
==.
(2)∵≤α<,又cos =>0,
∴<α+<,
∴sin=-=-,
从而cos 2α=sin=2sincos
=-,
sin 2α=-cos=1-2cos2=.
∴cos=cos 2αcos-sin 2αsin=(cos 2α-sin 2α)=×=-.
(3)∵0
利用诱导公式,sin=cos
=cos=.
∴原式==
=2sin=.
思维升华 解决给值求值问题的方法
(1)有方向地将已知式或未知式化简,使关系明朗化;寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
(2)当遇到±x这样的角时可利用互余角的关系和诱导公式,将条件与结论沟通.
【训练2】 设α为锐角,若cos=,则sin的值为________.
答案
解析 ∵α为锐角,∴<α+<.
∵cos=,∴sin=,
∴sin=sin
=2sincos
=2××=,
cos=cos
=2cos2-1
=2×-1=,
∴sin=sin
=sincos-cossin
=×=×=.
题型三 三角函数式的化简与证明
角度1 三角恒等式的证明问题
【例3-1】 求证:=tan4 A.
证明 ∵左边=
===(tan2A)2
=tan4 A=右边,
∴=tan4 A.
角度2 三角函数式的化简问题
【例3-2】 化简:.
解
=
=·
=sin x·=tan x.
思维升华 探究三角函数式化简、证明的常用技巧
(1)特殊角的三角函数与特殊值的互化;
(2)对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分;
(3)对于二次根式,注意倍角公式的逆用;
(4)利用角与角之间的隐含关系,如互余、互补等;
(5)利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
【训练3】 (1)求证:=.
(2)化简·.
(1)证明 原式变形为1+sin 4θ-cos 4θ
=tan 2θ(1+sin 4θ+cos 4θ),(*)
而(*)式右边=tan 2θ(1+cos 4θ+sin 4θ)
=(2cos22θ+2sin 2θcos 2θ)
=2sin 2θcos 2θ+2sin22θ
=sin 4θ+1-cos 4θ
=左边,
∴(*)式成立,即原式得证.
(2)解 原式=·
=·
=·=2.
1.倍角公式中的“倍角”是相对的,对于两个角的比值等于2的情况都成立,如6α是3α的2倍,3α是的2倍……这里蕴含着换元思想.这就是说,“倍”是相对而言的,是描述两个数量之间的关系的.
2.在二倍角公式中,二倍角的余弦公式最为灵活多样,应用广泛,二倍角的常用形式:①1+cos 2α=2cos2α,②cos2α=,③1-cos 2α=2sin2α,④sin2α=.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
