苏科版数学八年级上册第三章《勾股定理》单元测试题(含解析)
文档属性
| 名称 | 苏科版数学八年级上册第三章《勾股定理》单元测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-16 17:17:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
苏科版数学八年级上册第三章勾股定理练习题
一、选择题(本大题共14小题,共42.0分)
已知一个直角三角形的两边长分别是3和4,则第三边长的平方是
A. 25 B. 7 C. 25或7 D. 5或12
如图,在中,,,,于D,则CD的长是
A. 5
B. 7
C.
D.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
A. 13
B. 26
C. 34
D. 47
若直角三角形两直角边长分别为5和12,则斜边的长为
A. 17 B. 7 C. 14 D. 13
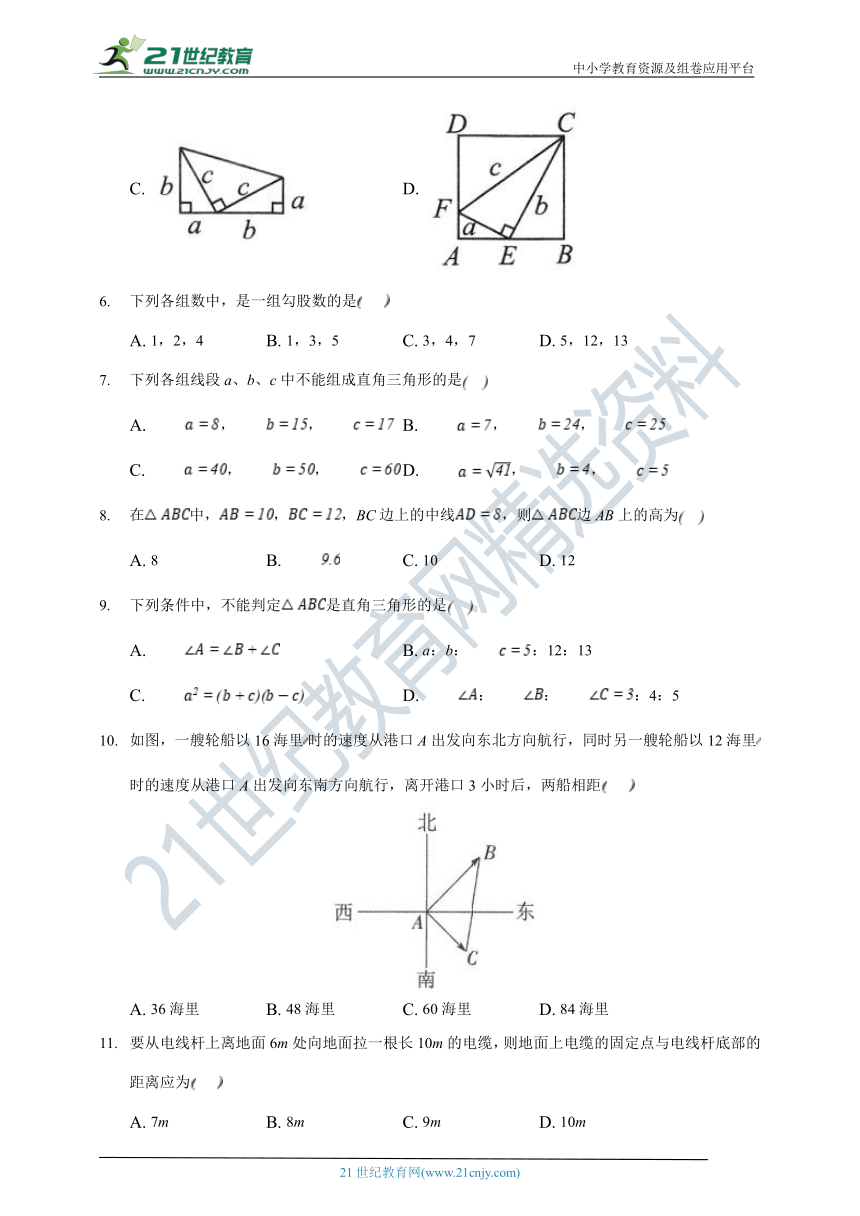
在图中,不能用来证明勾股定理的是
A. B.
C. D.
下列各组数中,是一组勾股数的是
A. 1,2,4 B. 1,3,5 C. 3,4,7 D. 5,12,13
下列各组线段a、b、c中不能组成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在中,,,BC边上的中线,则边AB上的高为
A. 8 B. C. 10 D. 12
下列条件中,不能判定是直角三角形的是
A. B. a:b::12:13
C. D. :::4:5
如图,一艘轮船以16海里时的速度从港口A出发向东北方向航行,同时另一艘轮船以12海里时的速度从港口A出发向东南方向航行,离开港口3小时后,两船相距
A. 36海里 B. 48海里 C. 60海里 D. 84海里
要从电线杆上离地面6m处向地面拉一根长10m的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A. 7m B. 8m C. 9m D. 10m
如图所示的一块地,已知,,,,,则这块地的面积为
A. B. C. D.
小明准备测量一段河水的深度,他把一根竹竿直插到离岸边6米远的水底,竹竿高出水面2米,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为
A. 7m B. 8m C. 9m D. 10m
如图,架在消防车上的云梯AB长为,,,云梯底部离地面的距离BC为,则云梯的顶端离地面的距离AE为
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
如图,在中,已知,,垂足为D,若E是AD的中点,则______.
如图所示的正方形是由四个全等的直角三角形拼成的,直角三角形的两条直角边长分别为2,3,则大正方形的面积为______.
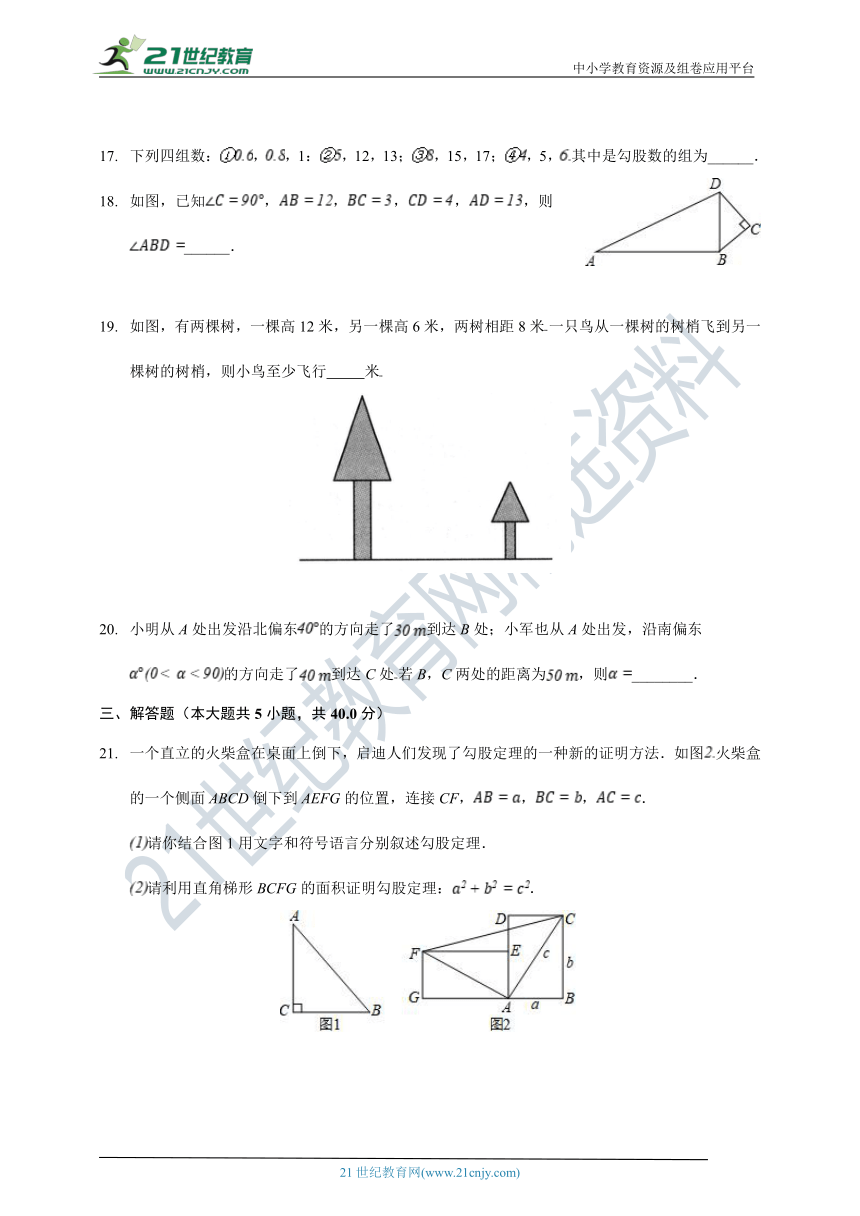
下列四组数:,,1:,12,13;,15,17;,5,其中是勾股数的组为______.
如图,已知,,,,,则______.
如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米
小明从A处出发沿北偏东的方向走了到达B处;小军也从A处出发,沿南偏东的方向走了到达C处若B,C两处的距离为,则________.
三、解答题(本大题共5小题,共40.0分)
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图火柴盒的一个侧面ABCD倒下到AEFG的位置,连接CF,,,.
请你结合图1用文字和符号语言分别叙述勾股定理.
请利用直角梯形BCFG的面积证明勾股定理:.
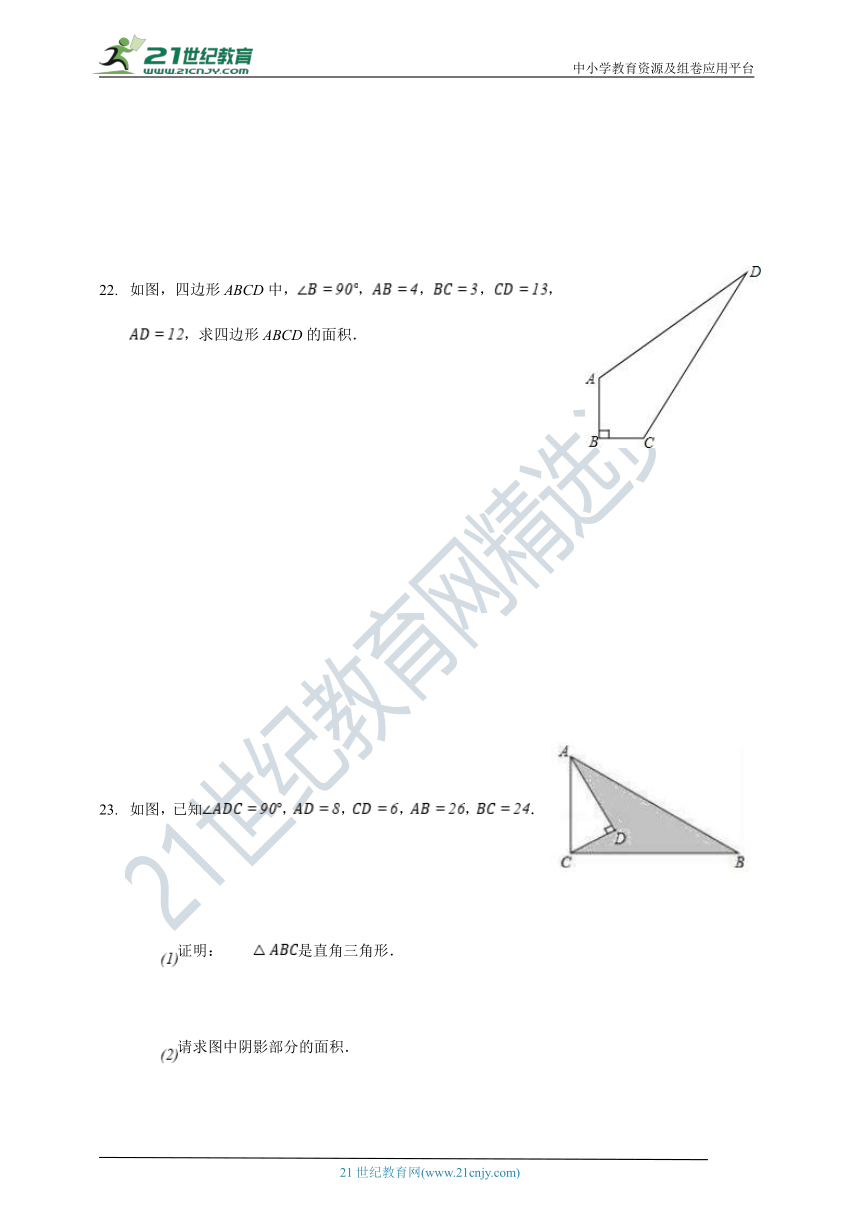
如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
如图,已知,,,,.
证明:是直角三角形.
请求图中阴影部分的面积.
有一辆载有集装箱的卡车,高米,宽米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是米.这辆卡车能否通过此桥洞?通过计算说明理由.
如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个记号,然后将绳子底端拉到离旗杆底端5米的地面处,发现此时绳子底端距离记号处1米,则旗杆的高度是多少米?
答案和解析
1.【答案】C
【解析】解:若3为一直角边长,4为斜边长,根据勾股定理得另一直角边长的平方为
若3、4是两条直角边长,根据勾股定理得斜边长的平方为,
所以第三边长的平方为25或7.
故选C.
2.【答案】C
【解析】解:在中,,,,
,
,
,
解得.
故选C.
3.【答案】D
【解析】解:如图,
由勾股定理得,正方形F的面积正方形A的面积正方形B的面积,
同理,正方形G的面积正方形C的面积正方形D的面积,
正方形E的面积正方形F的面积正方形G的面积,
故选:D.
4.【答案】D
【解析】解:由勾股定理可得:斜边,
故选:D.
利用勾股定理可以求出斜边即可.
5.【答案】D
【解析】略
6.【答案】D
【解析】解:,且5、12、13都是正整数,
、12、13是一组勾股数.
故选:D.
7.【答案】C
【解析】解:A、因为,所以能组成直角三角形;
B、因为,所以能组成直角三角形;
C、因为,所以不能组成直角三角形;
D、因为,所以能组成直角三角形.
故选:C.
8.【答案】B
【解析】解:如图,作于E.
是的中线,,
,
,,,
,
,
是直角三角形,且,
,
,
,
故选:B.
9.【答案】D
【解析】解:A、,,
,
为直角三角形,故此选项不合题意;
B、,
能构成直角三角形,故此选项不符合题意;
C、,即,
,
能构成直角三角形,故此选项不符合题意;
D、设,,,
,
解得:,
则,
不是直角三角形,故此选项符合题意.
故选:D.
10.【答案】C
【解析】略
11.【答案】B
【解析】略
12.【答案】A
解析】解:如图,连接AC.
在中,,,,
,
又,
是直角三角形,
这块地的面积
故选:A.
13.【答案】B
【解析】解:在直角中,.
设河深,则.
根据勾股定理得出:
解得:.
即河水的深度为8m,
故选:B.
河水的深、竹竿的长、离岸的距离三者构成直角三角形,作出图形,根据勾股定理即可求解.
本题主要考查了勾股定理在实际生活中的应用,根据勾股定理可以把求线段的长的问题转化为解方程得问题解决.
14.【答案】B
【解析】
解:设AD为xm,
,
为,
长为,
在中,
,
解得,不符合题意,舍去
.
故选B.
15.【答案】1
【解析】解:设,,
是AD的中点,
,,
,
,
,
,
在中,由勾股定理得:
,
,
,
,
在中,由勾股定理得:
,
,
,
故答案为:1
16.【答案】13
【解析】解:直角三角形的两条直角边长分别为2,3,
斜边为,即大正方形的边长为,
大正方形的面积为.
故答案为:13.
17.【答案】2
【解析】解:,不是整数,不是勾股数;
,是勾股数;
,是勾股数;
,不是勾股数;
其中是勾股数的组为2.
故答案为:2.
满足的三个正整数,称为勾股数,依此即可求解.
此题主要考查了勾股数,注意:三个数必须是正整数.一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.记住常用的勾股数再做题可以提高速度.
18.【答案】
【解析】解:在直角中,,,,
,
在中,,
,
故答案为:.
先在直角中运用勾股定理求出,然后根据勾股定理的逆定理得出.
19.【答案】10
【解析】
如图,过点B作于C,
在中,由勾股定理,得,
米,即小鸟至少飞行10米
20.【答案】50
【解析】解:,,,
,
,
,
,
故答案为:50.
21.【答案】解:直角三角形两直角边的平方和等于斜边的平方.
中,,,,,则有.
,
,
,
整理得:.
22.【答案】解:连结AC,
在中,
,,,
,
,
在中,
,,,
,
是直角三角形,
四边形ABCD的面积.
23.【答案】证明:在中,,,,
,
取正值.
在中,,,
,
为直角三角形;
解:
.
24.【答案】解:如图,M,N为卡车的宽度,
过M,N作AB的垂线交半圆于C,D,过O作,E为垂足,
米,米,
由作法得,米,
又米,
在中,米,
.
这辆卡车能通过.
25.【答案】解:如图,设旗杆的高度为,则,,,
在中,,
解得,
答:旗杆的高度是12m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏科版数学八年级上册第三章勾股定理练习题
一、选择题(本大题共14小题,共42.0分)
已知一个直角三角形的两边长分别是3和4,则第三边长的平方是
A. 25 B. 7 C. 25或7 D. 5或12
如图,在中,,,,于D,则CD的长是
A. 5
B. 7
C.
D.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
A. 13
B. 26
C. 34
D. 47
若直角三角形两直角边长分别为5和12,则斜边的长为
A. 17 B. 7 C. 14 D. 13
在图中,不能用来证明勾股定理的是
A. B.
C. D.
下列各组数中,是一组勾股数的是
A. 1,2,4 B. 1,3,5 C. 3,4,7 D. 5,12,13
下列各组线段a、b、c中不能组成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在中,,,BC边上的中线,则边AB上的高为
A. 8 B. C. 10 D. 12
下列条件中,不能判定是直角三角形的是
A. B. a:b::12:13
C. D. :::4:5
如图,一艘轮船以16海里时的速度从港口A出发向东北方向航行,同时另一艘轮船以12海里时的速度从港口A出发向东南方向航行,离开港口3小时后,两船相距
A. 36海里 B. 48海里 C. 60海里 D. 84海里
要从电线杆上离地面6m处向地面拉一根长10m的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A. 7m B. 8m C. 9m D. 10m
如图所示的一块地,已知,,,,,则这块地的面积为
A. B. C. D.
小明准备测量一段河水的深度,他把一根竹竿直插到离岸边6米远的水底,竹竿高出水面2米,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为
A. 7m B. 8m C. 9m D. 10m
如图,架在消防车上的云梯AB长为,,,云梯底部离地面的距离BC为,则云梯的顶端离地面的距离AE为
A. B. C. D.
二、填空题(本大题共6小题,共18.0分)
如图,在中,已知,,垂足为D,若E是AD的中点,则______.
如图所示的正方形是由四个全等的直角三角形拼成的,直角三角形的两条直角边长分别为2,3,则大正方形的面积为______.
下列四组数:,,1:,12,13;,15,17;,5,其中是勾股数的组为______.
如图,已知,,,,,则______.
如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米
小明从A处出发沿北偏东的方向走了到达B处;小军也从A处出发,沿南偏东的方向走了到达C处若B,C两处的距离为,则________.
三、解答题(本大题共5小题,共40.0分)
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图火柴盒的一个侧面ABCD倒下到AEFG的位置,连接CF,,,.
请你结合图1用文字和符号语言分别叙述勾股定理.
请利用直角梯形BCFG的面积证明勾股定理:.
如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
如图,已知,,,,.
证明:是直角三角形.
请求图中阴影部分的面积.
有一辆载有集装箱的卡车,高米,宽米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是米.这辆卡车能否通过此桥洞?通过计算说明理由.
如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个记号,然后将绳子底端拉到离旗杆底端5米的地面处,发现此时绳子底端距离记号处1米,则旗杆的高度是多少米?
答案和解析
1.【答案】C
【解析】解:若3为一直角边长,4为斜边长,根据勾股定理得另一直角边长的平方为
若3、4是两条直角边长,根据勾股定理得斜边长的平方为,
所以第三边长的平方为25或7.
故选C.
2.【答案】C
【解析】解:在中,,,,
,
,
,
解得.
故选C.
3.【答案】D
【解析】解:如图,
由勾股定理得,正方形F的面积正方形A的面积正方形B的面积,
同理,正方形G的面积正方形C的面积正方形D的面积,
正方形E的面积正方形F的面积正方形G的面积,
故选:D.
4.【答案】D
【解析】解:由勾股定理可得:斜边,
故选:D.
利用勾股定理可以求出斜边即可.
5.【答案】D
【解析】略
6.【答案】D
【解析】解:,且5、12、13都是正整数,
、12、13是一组勾股数.
故选:D.
7.【答案】C
【解析】解:A、因为,所以能组成直角三角形;
B、因为,所以能组成直角三角形;
C、因为,所以不能组成直角三角形;
D、因为,所以能组成直角三角形.
故选:C.
8.【答案】B
【解析】解:如图,作于E.
是的中线,,
,
,,,
,
,
是直角三角形,且,
,
,
,
故选:B.
9.【答案】D
【解析】解:A、,,
,
为直角三角形,故此选项不合题意;
B、,
能构成直角三角形,故此选项不符合题意;
C、,即,
,
能构成直角三角形,故此选项不符合题意;
D、设,,,
,
解得:,
则,
不是直角三角形,故此选项符合题意.
故选:D.
10.【答案】C
【解析】略
11.【答案】B
【解析】略
12.【答案】A
解析】解:如图,连接AC.
在中,,,,
,
又,
是直角三角形,
这块地的面积
故选:A.
13.【答案】B
【解析】解:在直角中,.
设河深,则.
根据勾股定理得出:
解得:.
即河水的深度为8m,
故选:B.
河水的深、竹竿的长、离岸的距离三者构成直角三角形,作出图形,根据勾股定理即可求解.
本题主要考查了勾股定理在实际生活中的应用,根据勾股定理可以把求线段的长的问题转化为解方程得问题解决.
14.【答案】B
【解析】
解:设AD为xm,
,
为,
长为,
在中,
,
解得,不符合题意,舍去
.
故选B.
15.【答案】1
【解析】解:设,,
是AD的中点,
,,
,
,
,
,
在中,由勾股定理得:
,
,
,
,
在中,由勾股定理得:
,
,
,
故答案为:1
16.【答案】13
【解析】解:直角三角形的两条直角边长分别为2,3,
斜边为,即大正方形的边长为,
大正方形的面积为.
故答案为:13.
17.【答案】2
【解析】解:,不是整数,不是勾股数;
,是勾股数;
,是勾股数;
,不是勾股数;
其中是勾股数的组为2.
故答案为:2.
满足的三个正整数,称为勾股数,依此即可求解.
此题主要考查了勾股数,注意:三个数必须是正整数.一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.记住常用的勾股数再做题可以提高速度.
18.【答案】
【解析】解:在直角中,,,,
,
在中,,
,
故答案为:.
先在直角中运用勾股定理求出,然后根据勾股定理的逆定理得出.
19.【答案】10
【解析】
如图,过点B作于C,
在中,由勾股定理,得,
米,即小鸟至少飞行10米
20.【答案】50
【解析】解:,,,
,
,
,
,
故答案为:50.
21.【答案】解:直角三角形两直角边的平方和等于斜边的平方.
中,,,,,则有.
,
,
,
整理得:.
22.【答案】解:连结AC,
在中,
,,,
,
,
在中,
,,,
,
是直角三角形,
四边形ABCD的面积.
23.【答案】证明:在中,,,,
,
取正值.
在中,,,
,
为直角三角形;
解:
.
24.【答案】解:如图,M,N为卡车的宽度,
过M,N作AB的垂线交半圆于C,D,过O作,E为垂足,
米,米,
由作法得,米,
又米,
在中,米,
.
这辆卡车能通过.
25.【答案】解:如图,设旗杆的高度为,则,,,
在中,,
解得,
答:旗杆的高度是12m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
