数学必修Ⅱ北师大版1.6垂直关系精品课件
文档属性
| 名称 | 数学必修Ⅱ北师大版1.6垂直关系精品课件 |  | |
| 格式 | zip | ||
| 文件大小 | 282.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-16 22:22:50 | ||
图片预览





文档简介
(共25张PPT)
垂直关系
习题课
垂直关系 习题课
复习与回顾
一 、线面垂直的定义和判定定理:
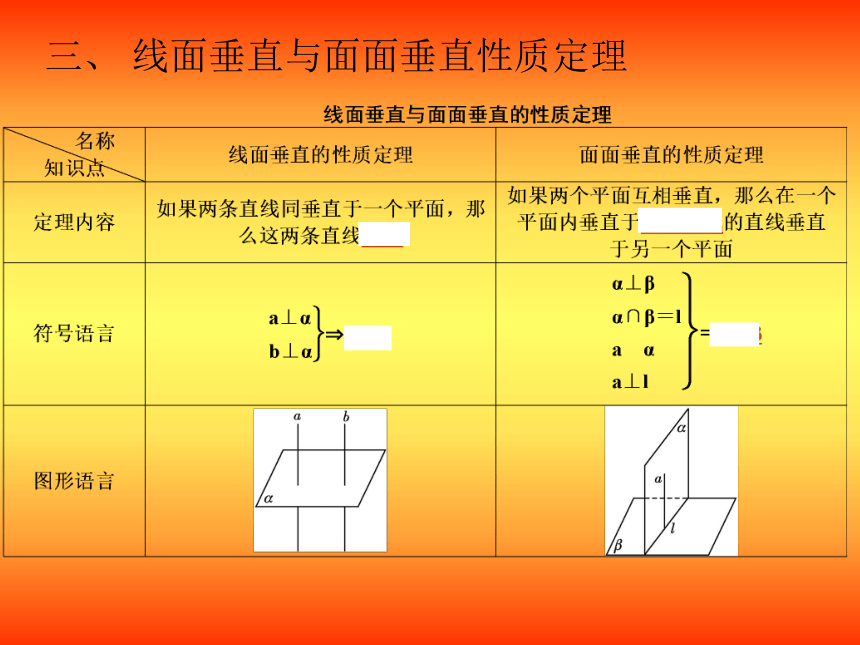
1.如果一条直线和一个平面内的 都垂直,那么称这条直线和这个平面 .
2.直线和平面垂直的判定定理:如果一条直线和一个平面内的 直线都垂直,那么该直线与此平面垂直.
任何一条直线
垂直
两条相交
二 、面面垂直的定义和判定定理:
1. 两个平面相交,如果所成的二面角是 ,就说这两个平面互相垂直.
2.平面和平面垂直的判定定理:如果一个平面经过另一个平面的 ,那么这两个平面互相垂直.
直二面角
一条垂线
三、 线面垂直与面面垂直性质定理
四、垂直关系的转化
线线垂直
面面垂直
线面垂直
判定
判定
性质
性质
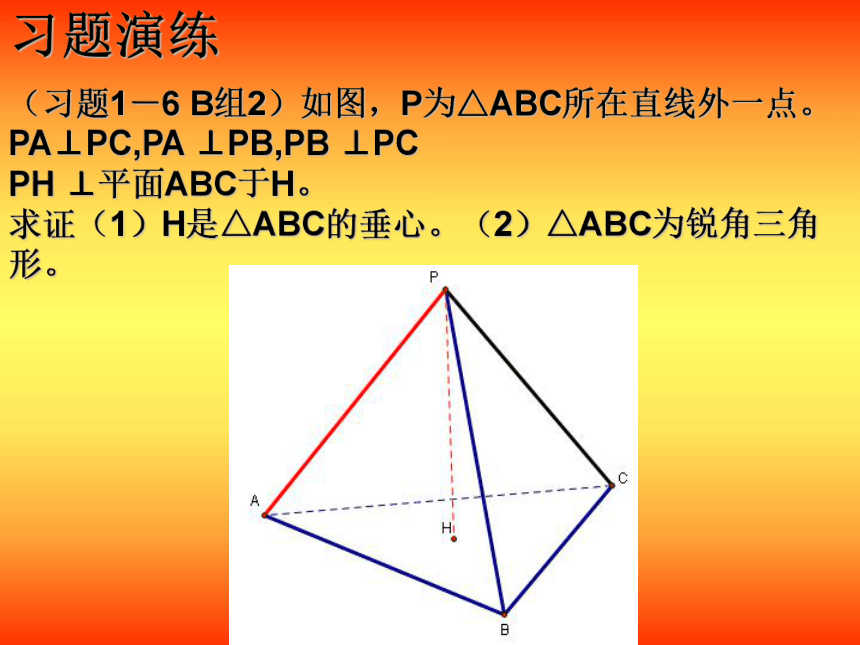
(习题1-6 B组2)如图,P为△ABC所在直线外一点。PA⊥PC,PA ⊥PB,PB ⊥PC
PH ⊥平面ABC于H。
求证(1)H是△ABC的垂心。(2)△ABC为锐角三角形。
习题演练
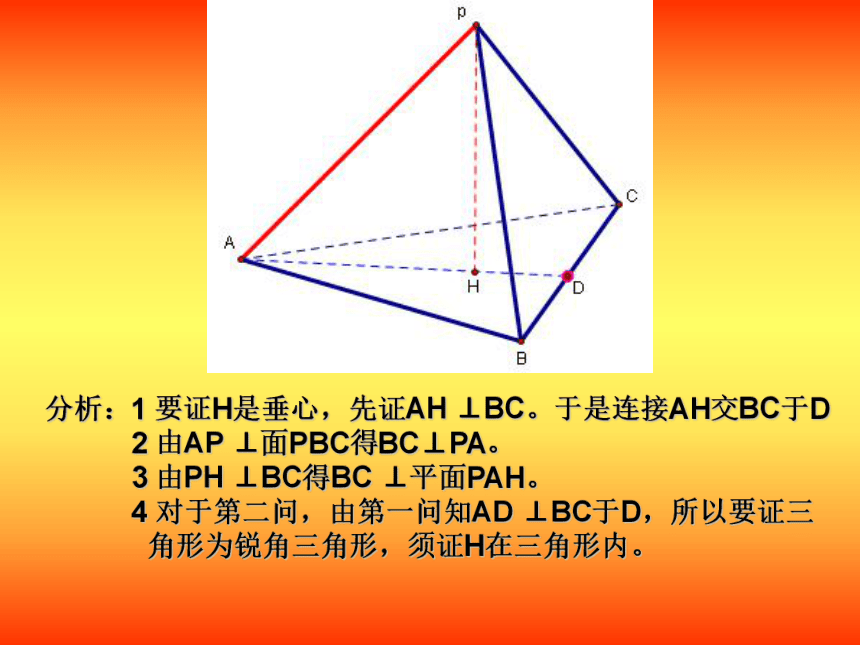
分析:1 要证H是垂心,先证AH ⊥BC。于是连接AH交BC于D
2 由AP ⊥面PBC得BC⊥PA。
3 由PH ⊥BC得BC ⊥平面PAH。
4 对于第二问,由第一问知AD ⊥BC于D,所以要证三
角形为锐角三角形,须证H在三角形内。
证明:(1)连接AH并延长交BC于D。
∴ ∵ PA⊥PB,PA ⊥PC,PA∩PC=P;
∴ PA ⊥平面PBC.
又∵BC
面PBC
∴ PA ⊥BC
∵PH ⊥平面ABC,BC
∴PH ⊥BC
∴BC ⊥平面PAH,而AH
∴BC ⊥AH.
同理,BH ⊥AC;CH ⊥AB.
∴H为△ABC的垂心。
平面ABC
平面PAH,
(2) 由已知,∠BPC=90°;连接PD,由第一问知PD ⊥BC
则D在线段BC上,又因为AD ⊥BC,从而∠ABC, ∠ACB都是锐角。
同理可证, ∠BAC也为锐角。故△ABC为锐角三角形。
(2)方法2:由图可知P在以AC为直径的圆上,AB>PA,BC>PC
∴B在以AC为直径的圆外。因此∠ABC为锐角。同理其余角也是锐角。
问题 1上题图形中有几个直角三角形?
引申与创新
问题 2 一个四面体中可以有四个直角三角形吗?
C
B
A
P
A
C
B
C
P
B
C
P
A
设计1
引申与创新
P
A
B
问题 2 一个四面体中可以有四个直角三角形吗?
设计2
如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,
引申与创新
B
A
C
设计3
问题 2 一个四面体中可以有四个直角三角形吗?
P
P
A
C
B
A
A
C
B
C
P
B
引申与创新
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究1 BC⊥平面PAC吗?
C
B
P
A
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究2 BC⊥PC吗?
探究3 △PBC为直角三角形吗?
C
B
P
A
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究4 图中有几个直角三角形?
C
B
A
P
A
C
B
C
P
P
A
B
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究5 面PBC⊥面PAC吗?
探究6 若AM⊥PC ,那么AM⊥平面PBC吗?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究7若AM⊥PC于M,AN⊥PB于N,连MN,则:(1)PB ⊥平面AMN吗?(2)PB ⊥MN吗?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究8 若AM⊥PC于M,AN⊥PB于N,连MN,则∠ANM是二面角A-PB-C的一个平面角吗?
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究9 图中互相垂直的平面有几对?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究10 若CQ ⊥ PB于Q,CS ⊥AB于S,连接QS。则 PB ⊥平面PQS吗?
开拓思维
拓展一 本节探究仅对设计1中垂直关系进行了探讨;还可以就点面距离,线面角,面面角等进行探一究。本题还可以以圆柱,棱柱等载体给出。
拓展二 对于设计2,还可就设计1所探究的10个方面进行同样探究;
拓展三 对于设计1,二面角A-PB-C的平面角如何做?
拓展四 研究边长为a的正四面体的距离和角、内切球外切球的半径。
解题反思
本节通过一道课本习题,引申到四直角四面体,并以此为载体对空间垂直关系进行探究,进而拓展到空间点线面关系的研究,给我们以下启示:
1 要善于对课本典型例题,习题和高考题进行联系思考。探究与创新是无止境的,以后还要继续进行。
2 只有善于创新,勇于探究,活学活用,培养能力,才能形成方法。
3 本节运用了化归等数学思想,平时要重视在数学思想指导下思考问题。
作业:
整理出设计1的10个探究问题;并仿此探究设计2.
思考题:拓展三,四.
引申与创新
C
B
P
A
P
P
A
C
B
A
A
C
B
C
P
谢谢大家!
垂直关系
习题课
垂直关系 习题课
复习与回顾
一 、线面垂直的定义和判定定理:
1.如果一条直线和一个平面内的 都垂直,那么称这条直线和这个平面 .
2.直线和平面垂直的判定定理:如果一条直线和一个平面内的 直线都垂直,那么该直线与此平面垂直.
任何一条直线
垂直
两条相交
二 、面面垂直的定义和判定定理:
1. 两个平面相交,如果所成的二面角是 ,就说这两个平面互相垂直.
2.平面和平面垂直的判定定理:如果一个平面经过另一个平面的 ,那么这两个平面互相垂直.
直二面角
一条垂线
三、 线面垂直与面面垂直性质定理
四、垂直关系的转化
线线垂直
面面垂直
线面垂直
判定
判定
性质
性质
(习题1-6 B组2)如图,P为△ABC所在直线外一点。PA⊥PC,PA ⊥PB,PB ⊥PC
PH ⊥平面ABC于H。
求证(1)H是△ABC的垂心。(2)△ABC为锐角三角形。
习题演练
分析:1 要证H是垂心,先证AH ⊥BC。于是连接AH交BC于D
2 由AP ⊥面PBC得BC⊥PA。
3 由PH ⊥BC得BC ⊥平面PAH。
4 对于第二问,由第一问知AD ⊥BC于D,所以要证三
角形为锐角三角形,须证H在三角形内。
证明:(1)连接AH并延长交BC于D。
∴ ∵ PA⊥PB,PA ⊥PC,PA∩PC=P;
∴ PA ⊥平面PBC.
又∵BC
面PBC
∴ PA ⊥BC
∵PH ⊥平面ABC,BC
∴PH ⊥BC
∴BC ⊥平面PAH,而AH
∴BC ⊥AH.
同理,BH ⊥AC;CH ⊥AB.
∴H为△ABC的垂心。
平面ABC
平面PAH,
(2) 由已知,∠BPC=90°;连接PD,由第一问知PD ⊥BC
则D在线段BC上,又因为AD ⊥BC,从而∠ABC, ∠ACB都是锐角。
同理可证, ∠BAC也为锐角。故△ABC为锐角三角形。
(2)方法2:由图可知P在以AC为直径的圆上,AB>PA,BC>PC
∴B在以AC为直径的圆外。因此∠ABC为锐角。同理其余角也是锐角。
问题 1上题图形中有几个直角三角形?
引申与创新
问题 2 一个四面体中可以有四个直角三角形吗?
C
B
A
P
A
C
B
C
P
B
C
P
A
设计1
引申与创新
P
A
B
问题 2 一个四面体中可以有四个直角三角形吗?
设计2
如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,
引申与创新
B
A
C
设计3
问题 2 一个四面体中可以有四个直角三角形吗?
P
P
A
C
B
A
A
C
B
C
P
B
引申与创新
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究1 BC⊥平面PAC吗?
C
B
P
A
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究2 BC⊥PC吗?
探究3 △PBC为直角三角形吗?
C
B
P
A
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究4 图中有几个直角三角形?
C
B
A
P
A
C
B
C
P
P
A
B
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究5 面PBC⊥面PAC吗?
探究6 若AM⊥PC ,那么AM⊥平面PBC吗?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究7若AM⊥PC于M,AN⊥PB于N,连MN,则:(1)PB ⊥平面AMN吗?(2)PB ⊥MN吗?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究8 若AM⊥PC于M,AN⊥PB于N,连MN,则∠ANM是二面角A-PB-C的一个平面角吗?
探究
B
C
P
A
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究9 图中互相垂直的平面有几对?
探究
对设计1就垂直关系进行探究,即PA⊥平面ABC,BC ⊥AC于C
探究10 若CQ ⊥ PB于Q,CS ⊥AB于S,连接QS。则 PB ⊥平面PQS吗?
开拓思维
拓展一 本节探究仅对设计1中垂直关系进行了探讨;还可以就点面距离,线面角,面面角等进行探一究。本题还可以以圆柱,棱柱等载体给出。
拓展二 对于设计2,还可就设计1所探究的10个方面进行同样探究;
拓展三 对于设计1,二面角A-PB-C的平面角如何做?
拓展四 研究边长为a的正四面体的距离和角、内切球外切球的半径。
解题反思
本节通过一道课本习题,引申到四直角四面体,并以此为载体对空间垂直关系进行探究,进而拓展到空间点线面关系的研究,给我们以下启示:
1 要善于对课本典型例题,习题和高考题进行联系思考。探究与创新是无止境的,以后还要继续进行。
2 只有善于创新,勇于探究,活学活用,培养能力,才能形成方法。
3 本节运用了化归等数学思想,平时要重视在数学思想指导下思考问题。
作业:
整理出设计1的10个探究问题;并仿此探究设计2.
思考题:拓展三,四.
引申与创新
C
B
P
A
P
P
A
C
B
A
A
C
B
C
P
谢谢大家!
