数学必修4北师大版1.7正切函数的图像和性质课件
文档属性
| 名称 | 数学必修4北师大版1.7正切函数的图像和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 424.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-16 22:22:50 | ||
图片预览




文档简介
(共23张PPT)
1.7 正切函数的图像和性质
北师大版必修4第一章三角函数
正弦,余弦函数的定义域
正弦,余弦函数的最值(值域)
正弦,余弦函数的奇偶性
正弦,余弦函数的单调性
正弦,余弦函数的周期(最小正周期)
正弦,余弦函数的图象
正弦,余弦函数性质的应用
请同学们想一想,对正弦和余弦函数,在作业和练习中,我们已涉及了多少类型的问题?
复习回顾:
类比正、余弦函数的定义,给出正切函数的定义
1.7 正切函数的图像和性质
回忆:怎样利用单位圆中的正弦线作出 y=sinx的图像?
1.7 正切函数的图像和性质
∴ 是周期函数, 是它的一个周期.
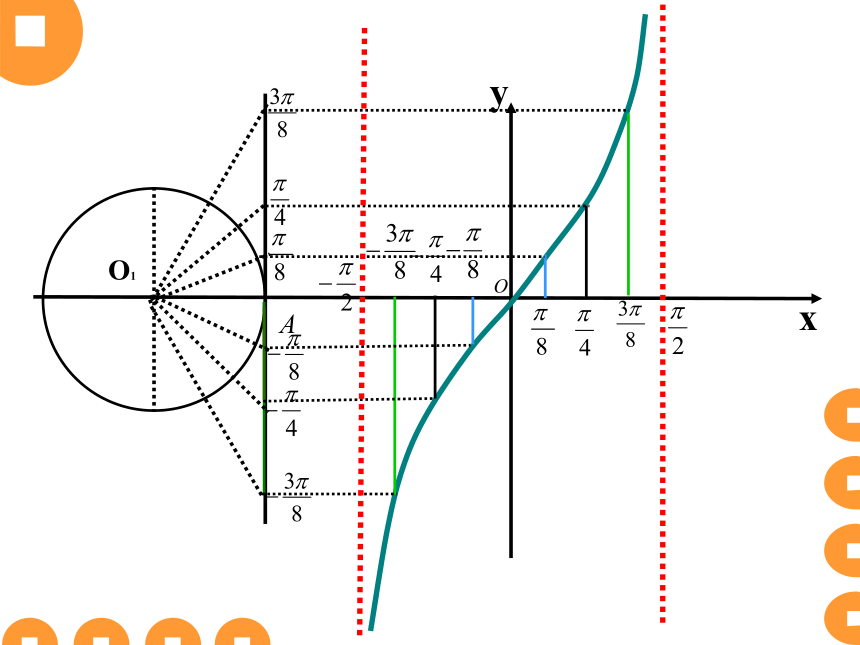
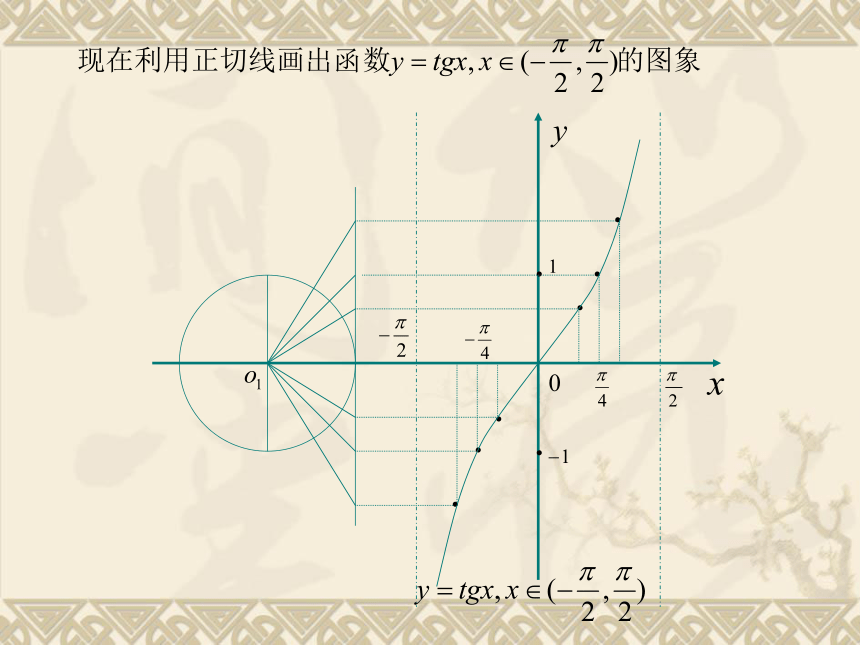
利用正切线画出函数 , 的图像:
正切函数 y=tgx 是否为周期函数?
x
y
O1
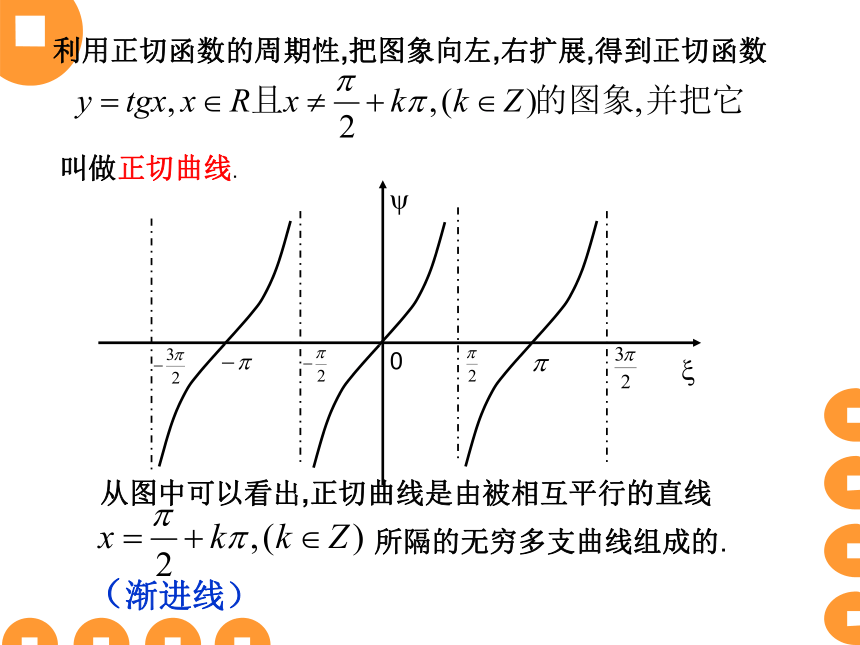
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线.
从图中可以看出,正切曲线是由被相互平行的直线
所隔的无穷多支曲线组成的.
x
y
0
(渐进线)
正切函数的主要性质如下:
定义域
值 域
周期性
奇偶性
单调性
实数集
奇函数(正切曲线关于原点对称)
例 题
例 题
例 题
例 题
例 题
能否说正切函数在定义域上单调增
返 回
返 回
x
y
0
1
-1
例3.求下列函数的周期.
返 回
例4.判断下列函数的奇偶性:
说明:函数具有奇.偶性的必要条件之一是定义域
关于原点对称,故验证f(-x)=f(-x)或
f(-x)= -f(x)成立前,要先判断定义域
是否关于原点对称.
返 回
例5.不通过求值,比较下列两个正切函数值的大小.
说明:比较两个正切型函数的大小,关键是把相应的角
诱导到y=tgx的同一单调区间内,利用y=tgx的
单调递增性来解决.
返 回
例6.求下列函数的单调区间:
返 回
1.7 正切函数的图像和性质
(1) 的作图是利用平移正切线得到的,当我们获得
上图像后,再利用周期性把该段图像向左右延伸、平移。
(2) 性质:
定义域
值域
周期
奇偶性
单调增区间
对称中心
渐近线方程
奇函数
小结:
1.7 正切函数的图像和性质
北师大版必修4第一章三角函数
正弦,余弦函数的定义域
正弦,余弦函数的最值(值域)
正弦,余弦函数的奇偶性
正弦,余弦函数的单调性
正弦,余弦函数的周期(最小正周期)
正弦,余弦函数的图象
正弦,余弦函数性质的应用
请同学们想一想,对正弦和余弦函数,在作业和练习中,我们已涉及了多少类型的问题?
复习回顾:
类比正、余弦函数的定义,给出正切函数的定义
1.7 正切函数的图像和性质
回忆:怎样利用单位圆中的正弦线作出 y=sinx的图像?
1.7 正切函数的图像和性质
∴ 是周期函数, 是它的一个周期.
利用正切线画出函数 , 的图像:
正切函数 y=tgx 是否为周期函数?
x
y
O1
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线.
从图中可以看出,正切曲线是由被相互平行的直线
所隔的无穷多支曲线组成的.
x
y
0
(渐进线)
正切函数的主要性质如下:
定义域
值 域
周期性
奇偶性
单调性
实数集
奇函数(正切曲线关于原点对称)
例 题
例 题
例 题
例 题
例 题
能否说正切函数在定义域上单调增
返 回
返 回
x
y
0
1
-1
例3.求下列函数的周期.
返 回
例4.判断下列函数的奇偶性:
说明:函数具有奇.偶性的必要条件之一是定义域
关于原点对称,故验证f(-x)=f(-x)或
f(-x)= -f(x)成立前,要先判断定义域
是否关于原点对称.
返 回
例5.不通过求值,比较下列两个正切函数值的大小.
说明:比较两个正切型函数的大小,关键是把相应的角
诱导到y=tgx的同一单调区间内,利用y=tgx的
单调递增性来解决.
返 回
例6.求下列函数的单调区间:
返 回
1.7 正切函数的图像和性质
(1) 的作图是利用平移正切线得到的,当我们获得
上图像后,再利用周期性把该段图像向左右延伸、平移。
(2) 性质:
定义域
值域
周期
奇偶性
单调增区间
对称中心
渐近线方程
奇函数
小结:
