数学必修Ⅳ北师大版1.7.1函数图象的变换课件
文档属性
| 名称 | 数学必修Ⅳ北师大版1.7.1函数图象的变换课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-16 00:00:00 | ||
图片预览








文档简介
(共56张PPT)
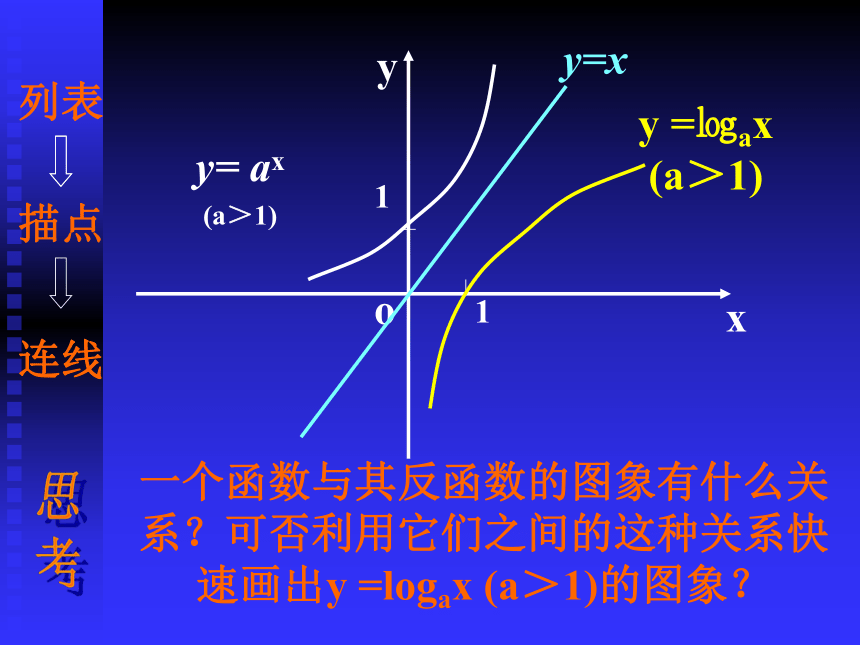
如何快速画出对数
函数y =㏒ax (a>1)
的大致图象
y
o
x
1
1
y =㏒ax (a>1)
y= ax
(a>1)
y=x
列表
描点
连线
一个函数与其反函数的图象有什么关系?可否利用它们之间的这种关系快速画出y =logax (a>1)的图象?
一、对称变换
请在同一坐标系内画出下列函数的图象.
(3) y = (-x+1)2
(2) y = - (x+1)2
(4) y = - (-x+1)2
(1) y = (x+1)2
做
做
看
观察函数图象(1),它与图象(2)、 (3)、 (4)分别有什么关系?
y=(-x+1)2
y=-(x+1)2
y=-(-x+1)2
(1). y=(x+1)2
做
看
关于x轴对称
关
于
y
轴
对
称
关于原点对称
(2)
(3)
(4)
(x, y)
(x, -y)
(-x, y)
(-x, -y)
做
看
(2)
(3)
(4)
想
y= f (x)
y= -f (x)
y= f (-x)
y= -f (-x)
关于x轴对称
关
于
y
轴
对
称
关于原点对称
返回
X
y
O
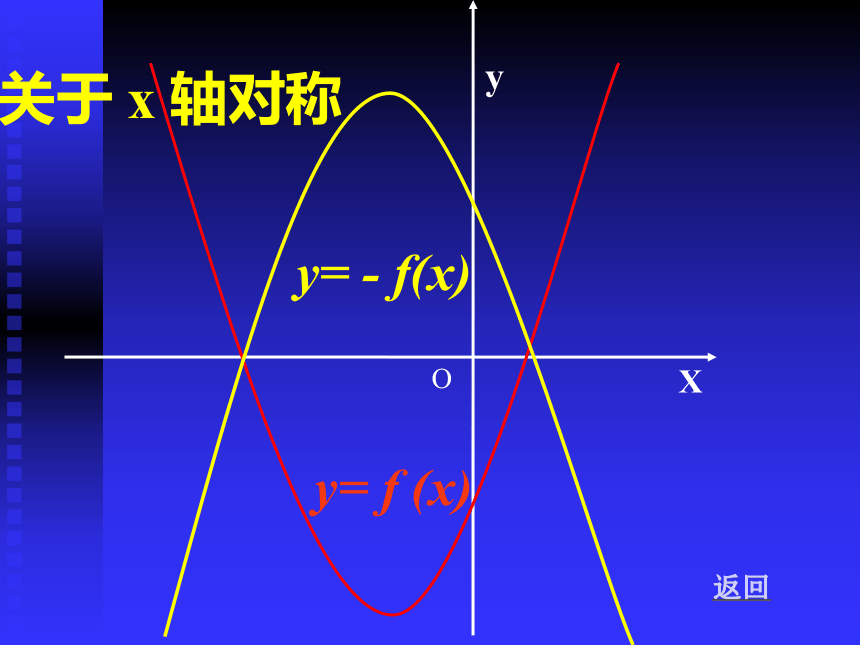
y= f (x)
y= - f(x)
关于 x 轴对称
返回
X
y
O
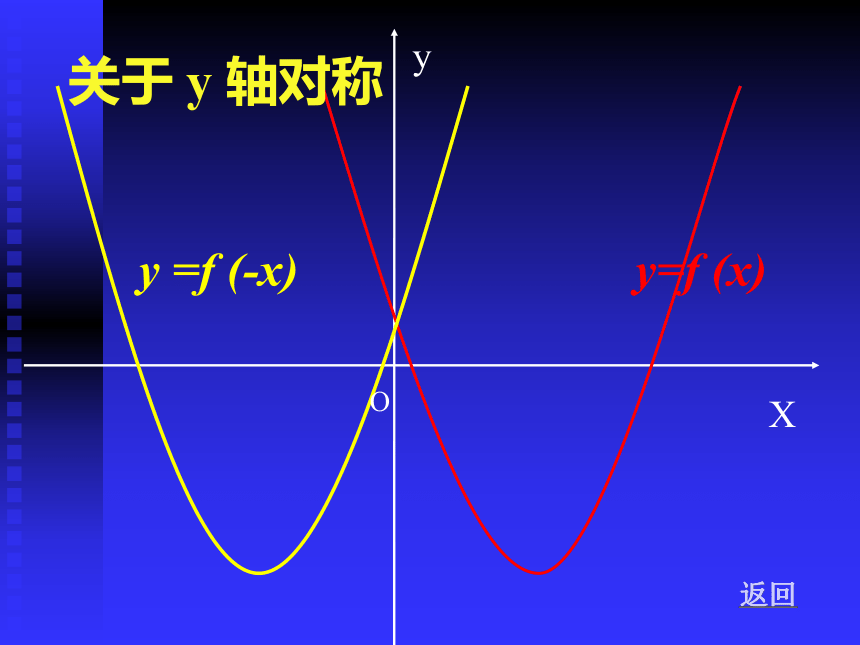
y=f (x)
y =f (-x)
关于 y 轴对称
返回
X
Y
O
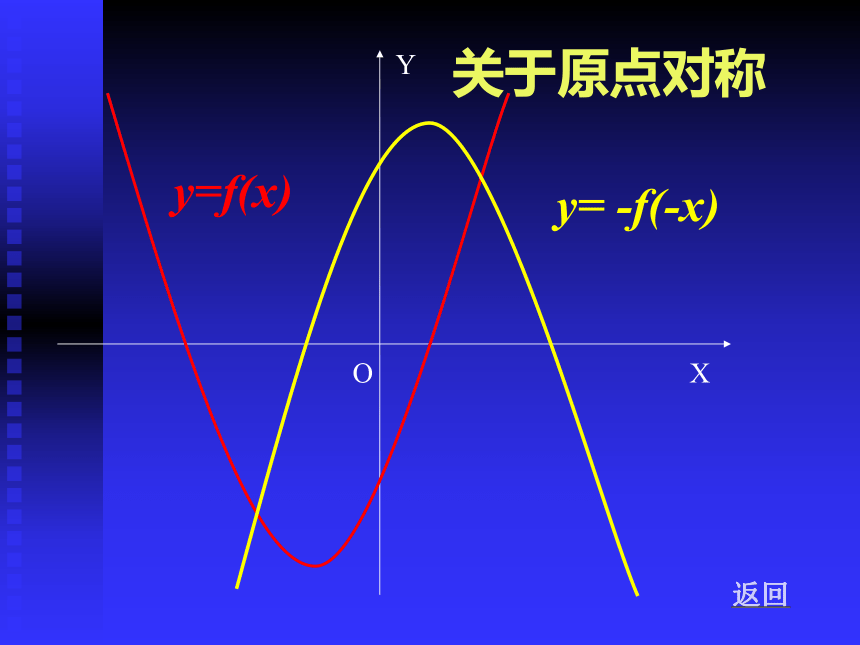
y=f(x)
y= -f(-x)
关于原点对称
返回
做
看
想
练
1、写出与函数 y = x 3-1
的图象关于x轴对称的图象
的解析式。
y = -x 3+1
做
看
想
练
2、写出与函数 y = x 3-1
的图象关于y轴对称的图象
的解析式。
y = -x 3-1
做
看
想
练
3、写出与函数 y = x 3-1的
图象关于原点对称的图象
的解析式。
y = x 3+1
二、?变换
请在同一坐标系内画出下列每组函数的图象。
1、
(1) y = x2
(2) y =( x+1)2
(3) y = (x-1)2
做
2、
(1) y = x2
(2) y = x2+1
(3) y = x2 - 1
做
看
观察函数图象(1),它与图象(2)、 (3) 分别有什么关系?
第 1 组图象
(1) y = x2
y =( x+1)2
y = (x-1)2
左移 1 个单位
右移 1个单位
做
看
(2)
(3)
(1) y = x2
y =( x+a)2
y = (x-a)2
左移 a 个单位
右移 a个单位
做
看
(2)
(3)
当a>0时,
想
若a < 0呢?
X
y
O
|a|
y = f(x)
y=f(x+a)
向左(a>0)或右(a<0)
平 移 |a| 个 单 位
二、平移变换
水平平移
做
看
观察函数图象(1),它与图象(2)、 (3)分别有什么关系?
第 2 组图象
二、平移变换
y = x2
y = x2
y = x2+1
y = x2 - 1
上移 1 个单位
下移 1 个单位
做
看
二、平移变换
y =f ( x) + a
y =f( x)
y = f (x ) -a
当a >0时,
向下平移
a个单位
思考:a <0呢?
y =f( x)
向上平移
a个单位
竖直平移
做
看
想
X
Y
O
|a|
y = f(x)
向上(a>0)下(a<0)
平 移 |a| 单 位
返回
y =f ( x) + a
1、如何完成下列函数图象的变换?
1
2
(1) f1(x)= - x2
1
2
向下平移
3个单位
f2(x) = - x2- 3
做
看
想
练
(2) f1(x)= x2
f2(x)= ( x-4)2
(3) f1(x)= x2
1
2
1
2
1
2
f2(x)= ( x-4)2+3
1
2
向右平移
4个单位
向右平移 4个单位,再沿 y轴向上平移 3个单位
做
看
想
练
2、 若函数 f(x)的图象过点(0,-1)则函数f(x+4)的反函数的图象经过点( )。
(A)
( B )
( C )
( D )
( 4,-1 )
(-1,-4 )
(-4,-1 )
(1,-4 )
B
做
看
想
练
3、要得到函数y = f (1- x ),只需将函数y =f ( - x )向——移动——个单位。
右
1
二、平移变换
做
看
想
练
(A)
(B)
(C)
(D)
再作关于直线 y = x对称的图象,
可得到函数 y=log2(x+1)的图象。
先向左平行移动1个单位
先向上平行移动1个单位
先向右平行移动1个单位
先向下平行移动1个单位
4、将函数 y=2 x的图象 ( )
D
三、?变换
请在同一坐标系内画出下列每组函数的图象。
1、
(1) y = (x-1 )2
(2) y =( | x |-1 )2
做
2、
(1) y = x2 - 1
(2)y = |x2-1 |
做
看
观察函数图象(1),它与图象(2)分别
有什么关系?
第 1 组图象
y = (|x|-1)2
(1) y =(x-1)2
保留 y轴右边图象 ,作其关于y轴对称图象,去掉 y轴左边部分
做
看
第 1 组图象
y = f ( |x|)
(1) y =f(x)
保留 y轴右边图象 ,作其关于y轴对称图象,去掉 y轴左边部分
三、翻折变换
左折变换
做
看
想
X
Y
O
y = f(x)
X
Y
O
保留 y轴右边图象,作其关于y轴
对称图象,去掉y轴左边部分
y = f ( |x|) ∣
y=f(x)
做
看
观察函数图象(1),它与图象(2)分别有什么关系?
第 2 组图象
(2) y = x2-1
y = |x2-1 |
保留x轴及其上 方图象,将
x轴下方图 象翻折上去
看
做
y = |f (x) |
(1) y =f(x)
三、翻折变换
上折变换
做
看
想
保留x轴及其上 方图象,将
x轴下方图 象翻折上去
X
Y
O
y = f(x)
O
X
Y
保留x轴上方图象,将x轴下方图象翻折上去
y=|f(x)|
三、翻折变换
A
B
o
o
y
y
x
x
1
1
1、函数 y= a︱x ︱ (a>1)的图象是( )。
做
看
想
练
x
y
o
o
y
C
D
函数 y= a︱x ︱ (a>1)的图象是( )。
1
x
D
练
做
看
想
如何画出函数y= lg ︱ x +1︱的图象。
1
y
x
o
y= lg ︱ x +1︱
y= lg ︱ x ︱
y= lg x
想
练
做
看
今天
我学到了什么
对称变换
图 象变 换
平移变换
翻折变换
水平变换
竖直变换
左折变换
上折变换
关于 x 轴
关于 y 轴
关于原点
知识内容
演示1
演示2
思想方法
数 形 结 合
积极的学习态度
想
练
做
看
自己探讨
自己发现
1、设有三个函数,第一个函数是 y=f (x),它的反函数是第二个函数,而第三个函数
与第二个函数的图象关于原点对称,那么
第三个函数是 ( )。
(A)
y=-f ( x )
(B)
(C)
(D)
y= f -1( - x )
y= f -1( x )
y=- f -1( - x )
C
2、作函数 y= ( )︱x -1 ︱ (a>1)的图象,并指出单调区间。
2
1
2、作函数 y= ( )︱x -1 ︱ (a>1)的
图象,并指出单调区间。
2
1
分析一:
y
o
x
1
1
y=( )︱x -1 ︱
2
1
y=( )︱x ︱
2
1
如图所示,
减区间是〔 1 , +∞ )。
增区间是(-∞,1〕,
3、已知 f(x) = lg x ,则 y = ︱f( 1-x)︱
的图象是( )。
y
1
o
x
3、已知 f(x) = lg x ,则 y = ︱f( 1-x )︱
的图象是( )。
y = ︱f( 1-x)︱= ︱ lg ( 1-x )︱
分析:
= ︱ lg ( 1-x )︱
y= lg x
y= lg〔- ( x-1 ) 〕
y= lg(- x )
把图象关于y轴对称
把图象向右平移1个单位
把轴下方部分沿x 轴翻折到上方
如何快速画出对数
函数y =㏒ax (a>1)
的大致图象
y
o
x
1
1
y =㏒ax (a>1)
y= ax
(a>1)
y=x
列表
描点
连线
一个函数与其反函数的图象有什么关系?可否利用它们之间的这种关系快速画出y =logax (a>1)的图象?
一、对称变换
请在同一坐标系内画出下列函数的图象.
(3) y = (-x+1)2
(2) y = - (x+1)2
(4) y = - (-x+1)2
(1) y = (x+1)2
做
做
看
观察函数图象(1),它与图象(2)、 (3)、 (4)分别有什么关系?
y=(-x+1)2
y=-(x+1)2
y=-(-x+1)2
(1). y=(x+1)2
做
看
关于x轴对称
关
于
y
轴
对
称
关于原点对称
(2)
(3)
(4)
(x, y)
(x, -y)
(-x, y)
(-x, -y)
做
看
(2)
(3)
(4)
想
y= f (x)
y= -f (x)
y= f (-x)
y= -f (-x)
关于x轴对称
关
于
y
轴
对
称
关于原点对称
返回
X
y
O
y= f (x)
y= - f(x)
关于 x 轴对称
返回
X
y
O
y=f (x)
y =f (-x)
关于 y 轴对称
返回
X
Y
O
y=f(x)
y= -f(-x)
关于原点对称
返回
做
看
想
练
1、写出与函数 y = x 3-1
的图象关于x轴对称的图象
的解析式。
y = -x 3+1
做
看
想
练
2、写出与函数 y = x 3-1
的图象关于y轴对称的图象
的解析式。
y = -x 3-1
做
看
想
练
3、写出与函数 y = x 3-1的
图象关于原点对称的图象
的解析式。
y = x 3+1
二、?变换
请在同一坐标系内画出下列每组函数的图象。
1、
(1) y = x2
(2) y =( x+1)2
(3) y = (x-1)2
做
2、
(1) y = x2
(2) y = x2+1
(3) y = x2 - 1
做
看
观察函数图象(1),它与图象(2)、 (3) 分别有什么关系?
第 1 组图象
(1) y = x2
y =( x+1)2
y = (x-1)2
左移 1 个单位
右移 1个单位
做
看
(2)
(3)
(1) y = x2
y =( x+a)2
y = (x-a)2
左移 a 个单位
右移 a个单位
做
看
(2)
(3)
当a>0时,
想
若a < 0呢?
X
y
O
|a|
y = f(x)
y=f(x+a)
向左(a>0)或右(a<0)
平 移 |a| 个 单 位
二、平移变换
水平平移
做
看
观察函数图象(1),它与图象(2)、 (3)分别有什么关系?
第 2 组图象
二、平移变换
y = x2
y = x2
y = x2+1
y = x2 - 1
上移 1 个单位
下移 1 个单位
做
看
二、平移变换
y =f ( x) + a
y =f( x)
y = f (x ) -a
当a >0时,
向下平移
a个单位
思考:a <0呢?
y =f( x)
向上平移
a个单位
竖直平移
做
看
想
X
Y
O
|a|
y = f(x)
向上(a>0)下(a<0)
平 移 |a| 单 位
返回
y =f ( x) + a
1、如何完成下列函数图象的变换?
1
2
(1) f1(x)= - x2
1
2
向下平移
3个单位
f2(x) = - x2- 3
做
看
想
练
(2) f1(x)= x2
f2(x)= ( x-4)2
(3) f1(x)= x2
1
2
1
2
1
2
f2(x)= ( x-4)2+3
1
2
向右平移
4个单位
向右平移 4个单位,再沿 y轴向上平移 3个单位
做
看
想
练
2、 若函数 f(x)的图象过点(0,-1)则函数f(x+4)的反函数的图象经过点( )。
(A)
( B )
( C )
( D )
( 4,-1 )
(-1,-4 )
(-4,-1 )
(1,-4 )
B
做
看
想
练
3、要得到函数y = f (1- x ),只需将函数y =f ( - x )向——移动——个单位。
右
1
二、平移变换
做
看
想
练
(A)
(B)
(C)
(D)
再作关于直线 y = x对称的图象,
可得到函数 y=log2(x+1)的图象。
先向左平行移动1个单位
先向上平行移动1个单位
先向右平行移动1个单位
先向下平行移动1个单位
4、将函数 y=2 x的图象 ( )
D
三、?变换
请在同一坐标系内画出下列每组函数的图象。
1、
(1) y = (x-1 )2
(2) y =( | x |-1 )2
做
2、
(1) y = x2 - 1
(2)y = |x2-1 |
做
看
观察函数图象(1),它与图象(2)分别
有什么关系?
第 1 组图象
y = (|x|-1)2
(1) y =(x-1)2
保留 y轴右边图象 ,作其关于y轴对称图象,去掉 y轴左边部分
做
看
第 1 组图象
y = f ( |x|)
(1) y =f(x)
保留 y轴右边图象 ,作其关于y轴对称图象,去掉 y轴左边部分
三、翻折变换
左折变换
做
看
想
X
Y
O
y = f(x)
X
Y
O
保留 y轴右边图象,作其关于y轴
对称图象,去掉y轴左边部分
y = f ( |x|) ∣
y=f(x)
做
看
观察函数图象(1),它与图象(2)分别有什么关系?
第 2 组图象
(2) y = x2-1
y = |x2-1 |
保留x轴及其上 方图象,将
x轴下方图 象翻折上去
看
做
y = |f (x) |
(1) y =f(x)
三、翻折变换
上折变换
做
看
想
保留x轴及其上 方图象,将
x轴下方图 象翻折上去
X
Y
O
y = f(x)
O
X
Y
保留x轴上方图象,将x轴下方图象翻折上去
y=|f(x)|
三、翻折变换
A
B
o
o
y
y
x
x
1
1
1、函数 y= a︱x ︱ (a>1)的图象是( )。
做
看
想
练
x
y
o
o
y
C
D
函数 y= a︱x ︱ (a>1)的图象是( )。
1
x
D
练
做
看
想
如何画出函数y= lg ︱ x +1︱的图象。
1
y
x
o
y= lg ︱ x +1︱
y= lg ︱ x ︱
y= lg x
想
练
做
看
今天
我学到了什么
对称变换
图 象变 换
平移变换
翻折变换
水平变换
竖直变换
左折变换
上折变换
关于 x 轴
关于 y 轴
关于原点
知识内容
演示1
演示2
思想方法
数 形 结 合
积极的学习态度
想
练
做
看
自己探讨
自己发现
1、设有三个函数,第一个函数是 y=f (x),它的反函数是第二个函数,而第三个函数
与第二个函数的图象关于原点对称,那么
第三个函数是 ( )。
(A)
y=-f ( x )
(B)
(C)
(D)
y= f -1( - x )
y= f -1( x )
y=- f -1( - x )
C
2、作函数 y= ( )︱x -1 ︱ (a>1)的图象,并指出单调区间。
2
1
2、作函数 y= ( )︱x -1 ︱ (a>1)的
图象,并指出单调区间。
2
1
分析一:
y
o
x
1
1
y=( )︱x -1 ︱
2
1
y=( )︱x ︱
2
1
如图所示,
减区间是〔 1 , +∞ )。
增区间是(-∞,1〕,
3、已知 f(x) = lg x ,则 y = ︱f( 1-x)︱
的图象是( )。
y
1
o
x
3、已知 f(x) = lg x ,则 y = ︱f( 1-x )︱
的图象是( )。
y = ︱f( 1-x)︱= ︱ lg ( 1-x )︱
分析:
= ︱ lg ( 1-x )︱
y= lg x
y= lg〔- ( x-1 ) 〕
y= lg(- x )
把图象关于y轴对称
把图象向右平移1个单位
把轴下方部分沿x 轴翻折到上方
