数学高二北师大版微积分学基本定理
图片预览



文档简介
(共19张PPT)
魏晋时期的刘徽著名的“割圆术”:
1、用积分的定义计算
的简要过程。
2、用积分的定义探究计算
。
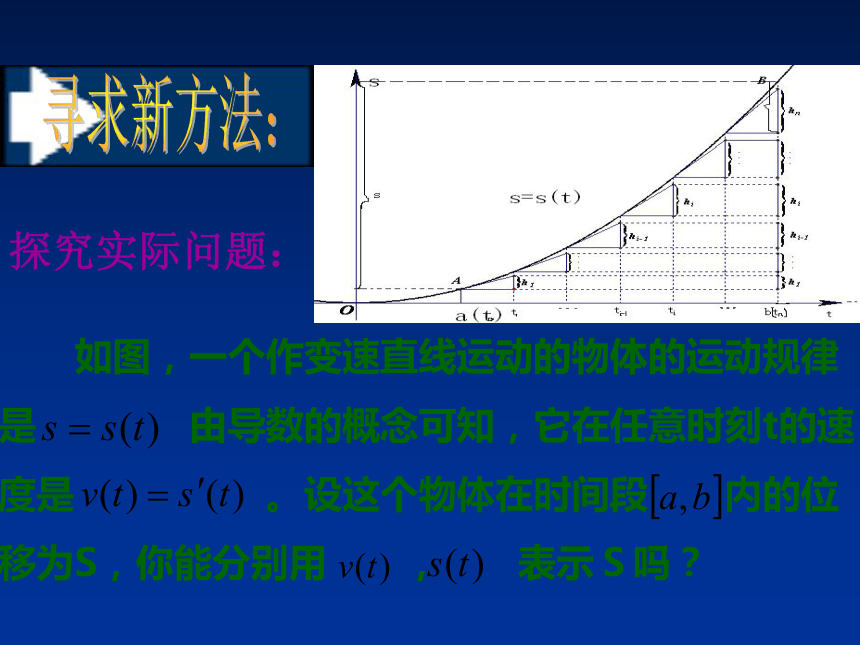
探究实际问题:
如图,一个作变速直线运动的物体的运动规律
是 由导数的概念可知,它在任意时刻t的速
度是 。设这个物体在时间段 内的位
移为S,你能分别用 , 表示S吗?
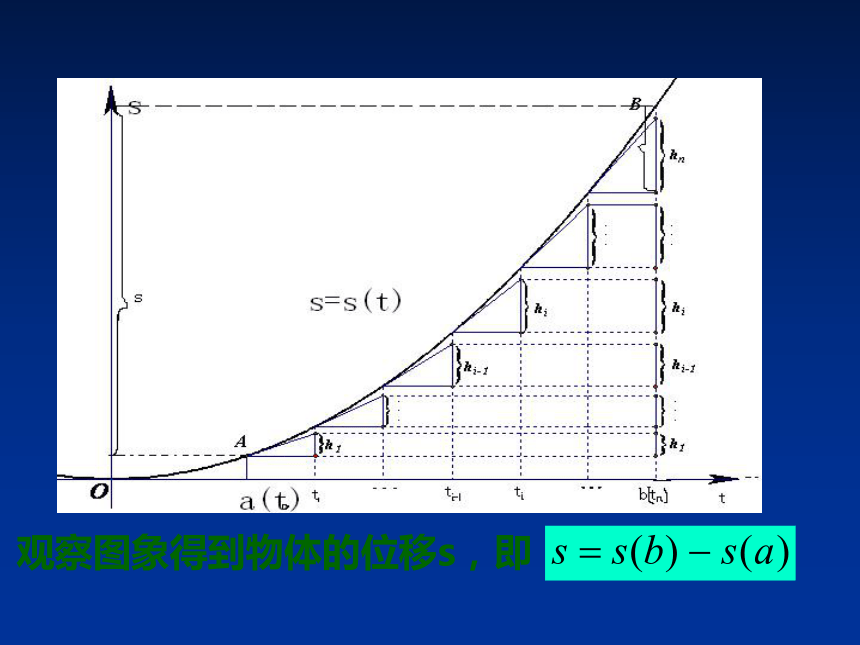
观察图象得到物体的位移s,即
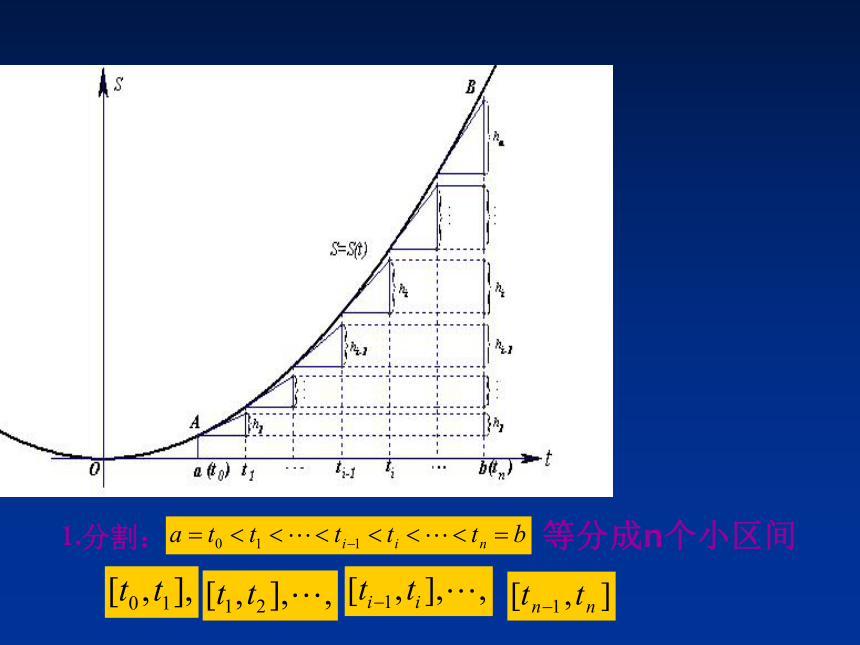
⒈分割: 等分成n个小区间
=
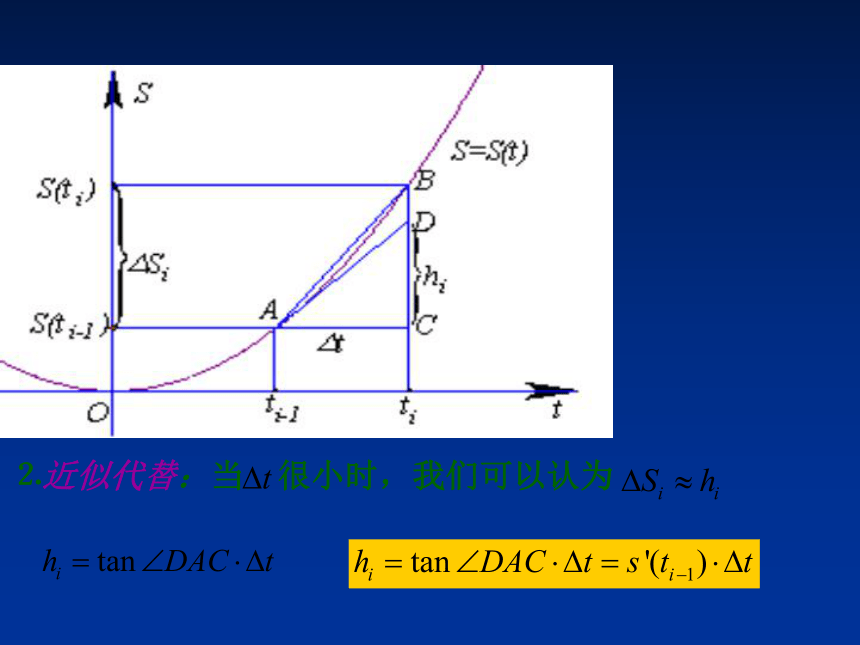
⒉近似代替:当 很小时,我们可以认为
⒊求和:
⒋取极限:物体的总位移的近似值
就越接近精确值S.
=
这不正是速度函数 的定积分吗?
归纳小结:上式表明,速度函数 在区间[a,b]
上的定积分等于位移函数 在区间[a,b]的右端
点处的函数值s(b)与左端点处的函数值s (a)之差.
式是否具有一般性呢?
微积分基本定理:
连续函数 f(x),若 ,则
即牛顿——莱布尼兹公式(Newton—Leibniz Formula)。
(1646-1716)
(1642-1727)
德国数学家-莱布尼茨
总之,定积分的几何意义:曲边梯形面积的代数和。
魏晋时期的刘徽著名的“割圆术”:
1、用积分的定义计算
的简要过程。
2、用积分的定义探究计算
。
探究实际问题:
如图,一个作变速直线运动的物体的运动规律
是 由导数的概念可知,它在任意时刻t的速
度是 。设这个物体在时间段 内的位
移为S,你能分别用 , 表示S吗?
观察图象得到物体的位移s,即
⒈分割: 等分成n个小区间
=
⒉近似代替:当 很小时,我们可以认为
⒊求和:
⒋取极限:物体的总位移的近似值
就越接近精确值S.
=
这不正是速度函数 的定积分吗?
归纳小结:上式表明,速度函数 在区间[a,b]
上的定积分等于位移函数 在区间[a,b]的右端
点处的函数值s(b)与左端点处的函数值s (a)之差.
式是否具有一般性呢?
微积分基本定理:
连续函数 f(x),若 ,则
即牛顿——莱布尼兹公式(Newton—Leibniz Formula)。
(1646-1716)
(1642-1727)
德国数学家-莱布尼茨
总之,定积分的几何意义:曲边梯形面积的代数和。
