数学必修II人教版直线与圆的位置关系课件
文档属性
| 名称 | 数学必修II人教版直线与圆的位置关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 748.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-16 22:22:50 | ||
图片预览





文档简介
(共28张PPT)
a(地平线)
●O
●O
●O
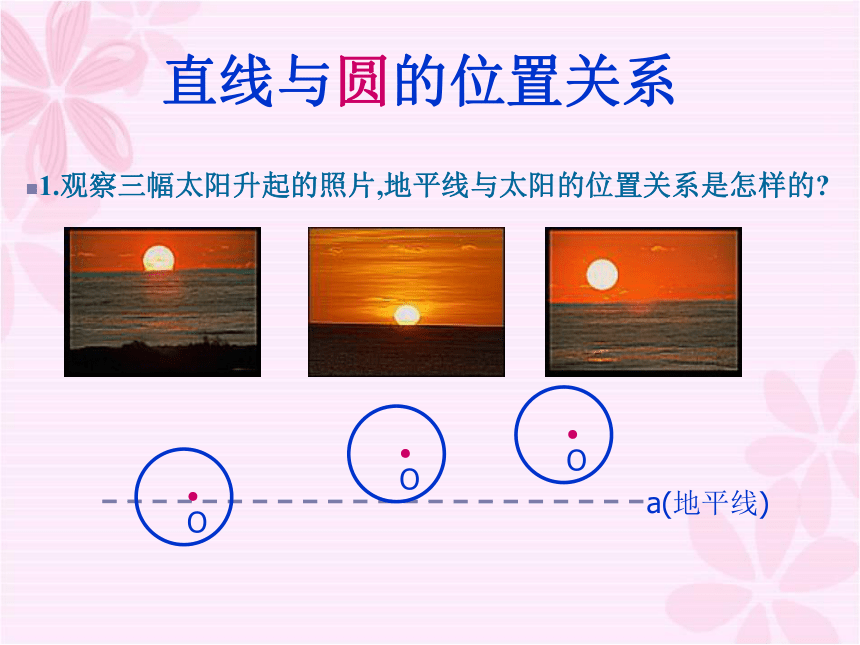
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
直线与圆的位置关系
直线与圆的位置关系
a(地平线)
●O
●O
●O
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
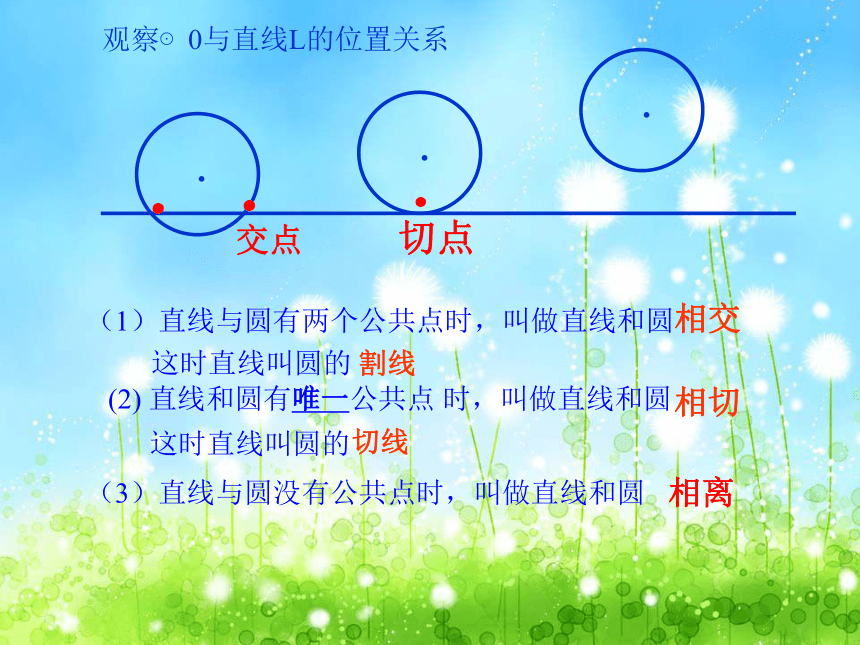
(2) 直线和圆有唯一公共点 时,叫做直线和圆
相切
这时直线叫圆的
切线
(1)直线与圆有两个公共点时,叫做直线和圆
这时直线叫圆的
割线
相交
观察⊙0与直线L的位置关系
(3)直线与圆没有公共点时,叫做直线和圆
相离
.
.
.
.
.
切点
.
交点
·O
·O
·O
·O
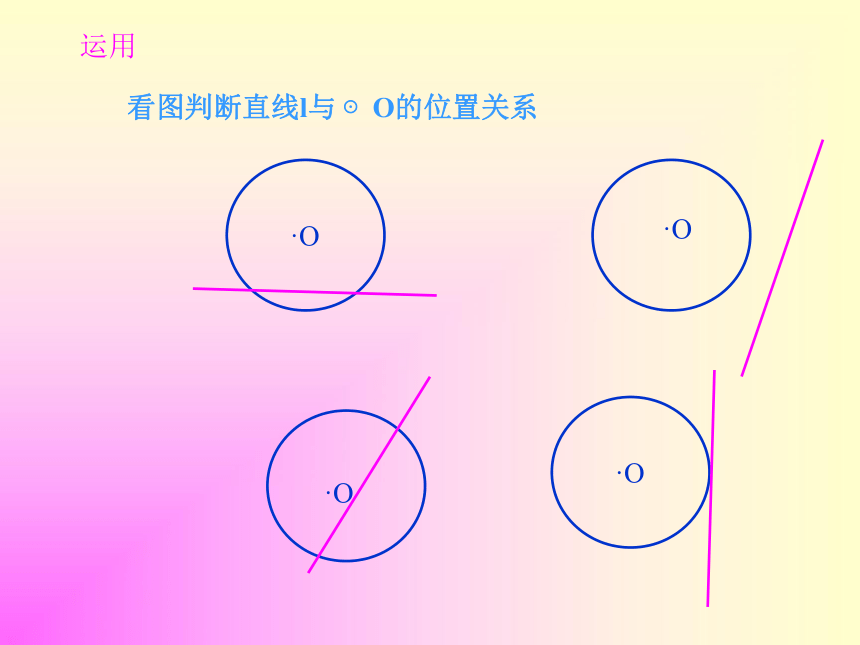
看图判断直线l与 ⊙O的位置关系
运用
.O
是是非非
1、直线与圆最多有两个公共
点 。………………( )
√
.O
是是非非
×
.C
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
是是非非
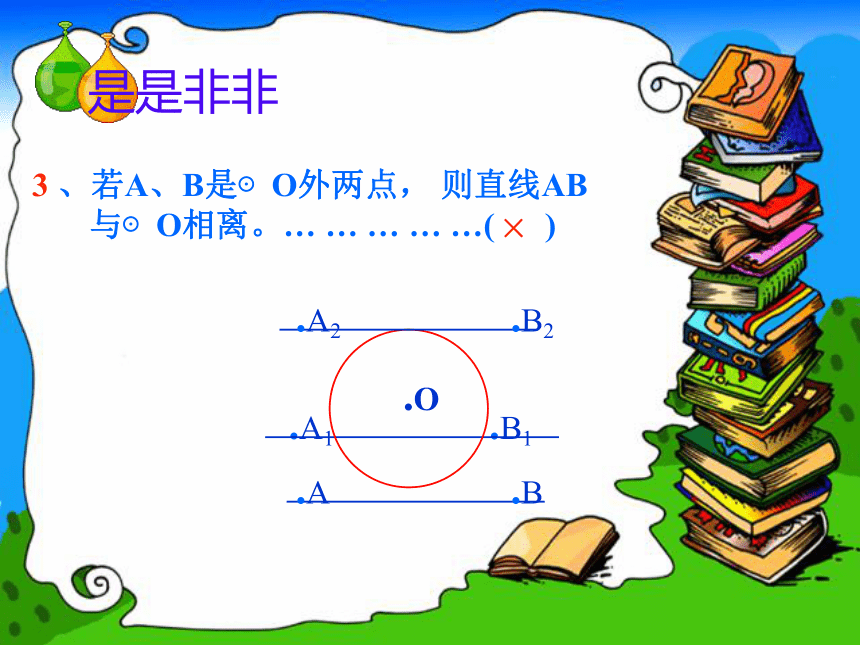
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
小问题:
能否根据基本概念来判断直线与圆的位置关系?
直线与圆的公共点的个数
小问题:
能否根据基本概念来判断直线与圆的位置关系?
直线与圆的公共点的个数
新的问题:
是否还有其它的方法来判断直线与圆的位置关系?
1、点与圆有几种位置关系?
复习提问:
2、怎样判定点和圆的位置关系?
.A
.A
.A
.A
.A
. B
.A
.A
.C
.A
.A
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
若将点改成直线 ,那么直线与圆的
位置关系又如何呢?
.O
a
b
c
直线与圆的位置关系
当d>r ,那么直线l与⊙O相离
当d=r ,那么直线l与⊙O相切
当dd表示圆心O到直线l的距离,r表示⊙O的半径
r
r
r
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d<
<
<
看一看想一想
当直线与圆
相离、相切、
相交时,d与
r有何关系?
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
练 习 (一)
填空:
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。直线a与⊙O的公共点个数是____
动动脑筋
相交
相切
两个
一个
3 已知⊙O的直径是6cm,O到直a的距离是4cm,则⊙O与直线a的位置关系是_____.
相离
练习(二):
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
C
D
说说收获
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
思考:圆心A到x轴、
y轴的距离各是多少
例题1:
.A
O
x
y
已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与x轴的位置关系是_____,⊙A与y轴的位置关系是______。
B
C
4
3
相离
相切
例2、在Rt
ABC中,∠ C=90°,AC=3cm, BC= 4cm,
圆心,r为半径的圆与AB有怎样的位置关系?
则以C为
(1)r =2cm, (2) r =2.4cm (3) r =3cm
C
A
B
3
4
圆心,r为半径的圆与AB有怎样的位置关系?
例2、在Rt
ABC中,∠ C=90°,AC=3cm, BC= 4cm,
则以C为
(1)r =2cm, (2) r =2.4cm (3)r=3cm
C
A
B
3
4
D
∵
∠ C=90°,AC=3cm, BC= 4cm,
解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∵S
ABC
=
AC×BC=
AB×CD
∴3×4 = 5×CD
∴
CD =
= 2.4
即d
(1)当r =2cm 时 , d > r
∴
圆与AB相离
(3)当r =3 cm 时 , d < r
∴
圆与AB相交
(2)当r =2.4cm 时 , d = r
∴
圆与AB相切
讨论:
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________ 时,⊙C与直线AB相切。
3、当r满足____________时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
0cmr=2.4cm
r>2.4cm
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
想一想
当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d1、直线与圆的位置关系3种:相离、相切和相交。
作业:102页1、2
希望大家如这朝阳,
越升越高!越升越亮!
作业:P86习题2----2A组 6
B组 1、2
a(地平线)
●O
●O
●O
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
直线与圆的位置关系
直线与圆的位置关系
a(地平线)
●O
●O
●O
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(2) 直线和圆有唯一公共点 时,叫做直线和圆
相切
这时直线叫圆的
切线
(1)直线与圆有两个公共点时,叫做直线和圆
这时直线叫圆的
割线
相交
观察⊙0与直线L的位置关系
(3)直线与圆没有公共点时,叫做直线和圆
相离
.
.
.
.
.
切点
.
交点
·O
·O
·O
·O
看图判断直线l与 ⊙O的位置关系
运用
.O
是是非非
1、直线与圆最多有两个公共
点 。………………( )
√
.O
是是非非
×
.C
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
是是非非
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
小问题:
能否根据基本概念来判断直线与圆的位置关系?
直线与圆的公共点的个数
小问题:
能否根据基本概念来判断直线与圆的位置关系?
直线与圆的公共点的个数
新的问题:
是否还有其它的方法来判断直线与圆的位置关系?
1、点与圆有几种位置关系?
复习提问:
2、怎样判定点和圆的位置关系?
.A
.A
.A
.A
.A
. B
.A
.A
.C
.A
.A
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
若将点改成直线 ,那么直线与圆的
位置关系又如何呢?
.O
a
b
c
直线与圆的位置关系
当d>r ,那么直线l与⊙O相离
当d=r ,那么直线l与⊙O相切
当d
r
r
r
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d
<
<
看一看想一想
当直线与圆
相离、相切、
相交时,d与
r有何关系?
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
练 习 (一)
填空:
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。直线a与⊙O的公共点个数是____
动动脑筋
相交
相切
两个
一个
3 已知⊙O的直径是6cm,O到直a的距离是4cm,则⊙O与直线a的位置关系是_____.
相离
练习(二):
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
C
D
说说收获
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
思考:圆心A到x轴、
y轴的距离各是多少
例题1:
.A
O
x
y
已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与x轴的位置关系是_____,⊙A与y轴的位置关系是______。
B
C
4
3
相离
相切
例2、在Rt
ABC中,∠ C=90°,AC=3cm, BC= 4cm,
圆心,r为半径的圆与AB有怎样的位置关系?
则以C为
(1)r =2cm, (2) r =2.4cm (3) r =3cm
C
A
B
3
4
圆心,r为半径的圆与AB有怎样的位置关系?
例2、在Rt
ABC中,∠ C=90°,AC=3cm, BC= 4cm,
则以C为
(1)r =2cm, (2) r =2.4cm (3)r=3cm
C
A
B
3
4
D
∵
∠ C=90°,AC=3cm, BC= 4cm,
解: 过C点作CD⊥AB,垂足为D
∴ AB = 5
∵S
ABC
=
AC×BC=
AB×CD
∴3×4 = 5×CD
∴
CD =
= 2.4
即d
(1)当r =2cm 时 , d > r
∴
圆与AB相离
(3)当r =3 cm 时 , d < r
∴
圆与AB相交
(2)当r =2.4cm 时 , d = r
∴
圆与AB相切
讨论:
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________ 时,⊙C与直线AB相切。
3、当r满足____________时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
0cm
r>2.4cm
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
想一想
当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm
(1)一种是根据定义进行识别:
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r 直线L与⊙o相离;
d=r 直线L与⊙o相切;
d
作业:102页1、2
希望大家如这朝阳,
越升越高!越升越亮!
作业:P86习题2----2A组 6
B组 1、2
