数学必修Ⅰ北师大版3.3.1指数函数的图像和性质课件
文档属性
| 名称 | 数学必修Ⅰ北师大版3.3.1指数函数的图像和性质课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 584.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-16 22:22:50 | ||
图片预览




文档简介
(共19张PPT)
指数函数
复习回顾
计算:
(1)
(2)
(3)
(4)
(5)
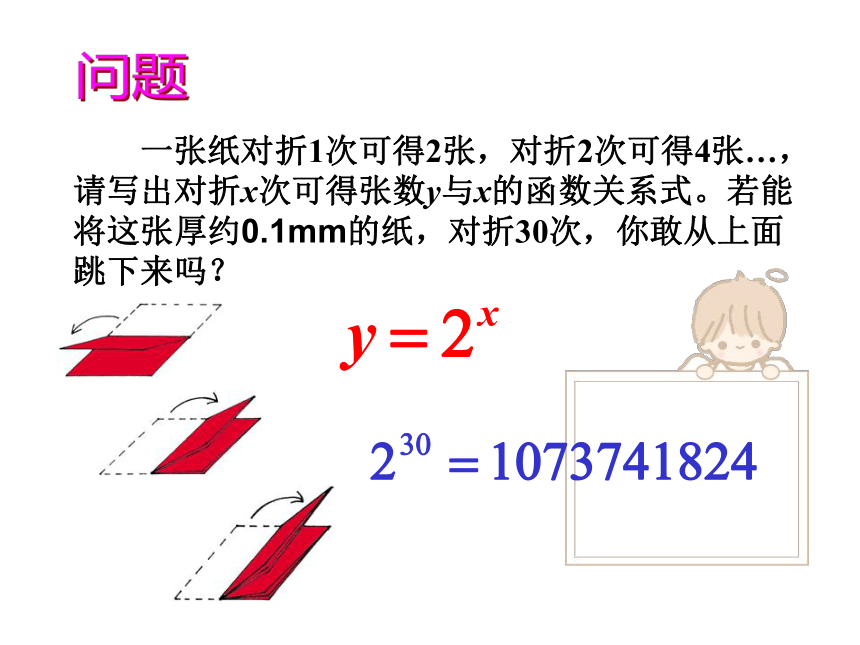
一张纸对折1次可得2张,对折2次可得4张…,请写出对折x次可得张数y与x的函数关系式。若能将这张厚约0.1mm的纸,对折30次,你敢从上面跳下来吗?
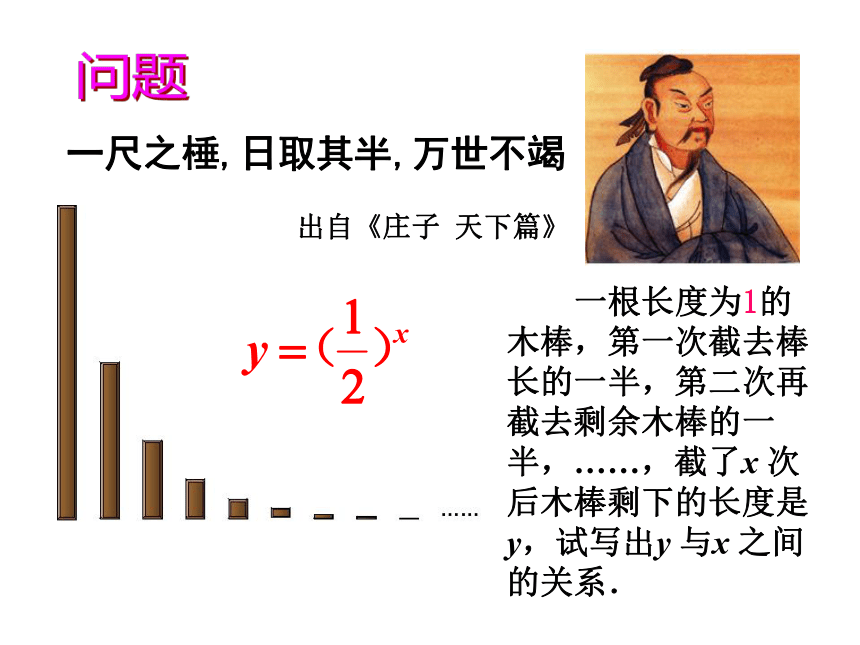
一根长度为1的木棒,第一次截去棒长的一半,第二次再截去剩余木棒的一半,……,截了x 次后木棒剩下的长度是 y,试写出y 与x 之间的关系.
一尺之棰,日取其半,万世不竭 。
出自《庄子 天下篇》
一般地,函数 叫指数函数,其中 x 是自变量.函数的定义域是R.
指数函数概念
思考:为何规定a 0,且a 1
判断下列哪些函数是指数函数?
√
×
×
×
×
√
√
×
0
1
1
0
1
1
0
1
1
0
1
0
1
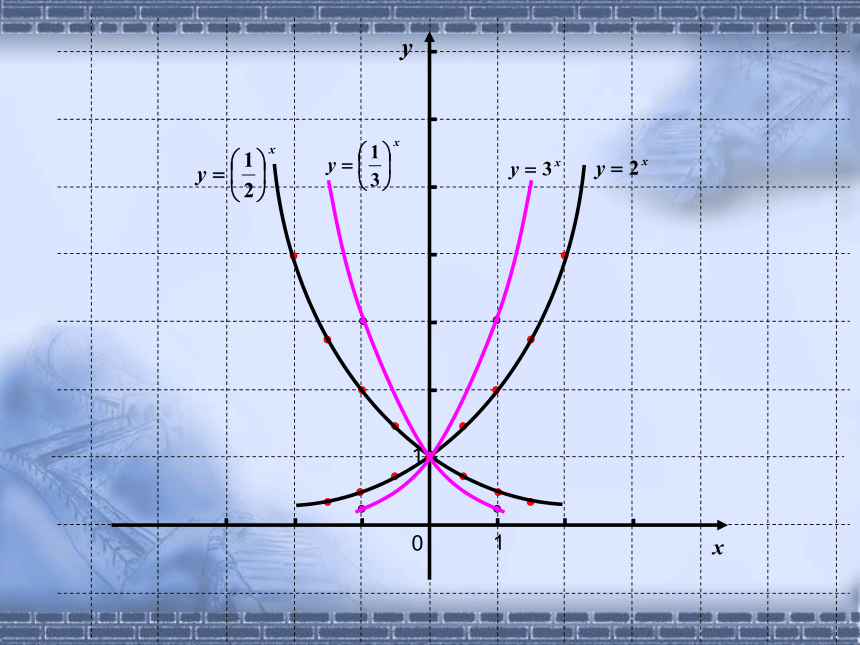
图
象
性
质
(1)定义域:
(2)值域:
(3)过点:
(4)
(4)
(5) (5)
a>1
0y=1
y
x
0
y=ax
(a>1)
当x>0或x<0时,
y的取值范围?
是 R 上的减函数
是 R 上的增函数
即 x = 0 时, y = 1 .
指数函数图象与性质
R
(0,+ ∞ )
当x>0或x<0时,
y的取值范围?
(0,1)
y=ax
(0x
0
y
当x>0时, 0< y<1
当x>0时, y>1
当x<0时, 0当x<0时, y>1
单调性
单调性
( 0 , 1 )
(0,1)
y=1
(0,1)
(0,1)
1.利用函数单调性比较下列各题中两个值的大小
指数函数例题
(2)
(3)
(1)
<
(1)
指数函数例题
解:考察指数函数 y=1.7x.
又∵指数2.5<3.
∴y=1.7x 是R上的增函数.
∵底数1.7 > 1
∴1.72.5<1.73.
(2)
<
指数函数例题
解:考察指数函数 y=0.8x.
又∵指数-0.1>-0.2.
∴y=0.8x 是R上的减函数.
∵底数 0 < 0.8 < 1
∴0.8-0.1<0.8-0.2.
>
(3)
指数函数例题
解:根据指数函数的性质,得:
且
从而有
(2)0.75-0.1 0.750.1 ;
指数函数练习
用“>”,“<”填空。
(1)30.8 30.7 ;
>
>
<
(3)2.3-1 0.8-0.5 .
(6)若am(5)若0.2m<0.2n,则m n;
(4)若2m<2n,则m n;
<
>
当0当 a>1 时, m n,
>
<
通过本节的学习,你对指数函数有什么认识?
指数函数
定义
数形结合
图像
性质
知识小结
指数函数练习
1. 设 ,则( )
A y3>y1>y2 B y2>y1>y3
C y1>y2>y3 D y1>y3>y2
2.函数y=ax-1 -3(a>0且a≠1)必过点 .
3.函数y=(a-1)x在R上是减函数,则a的取值范围是( )
4.已知 ,则a的取值范围是 ( )
C
D
A
5. 函数y=(3a-1)x为指数函数,则 .
学习的秘密在于
勤动脑
勤动手
作业:
(1)习题3-3 A组 4.(2),(4)
B组 3
(2)阅读课本111页C组第2题《富兰克林的遗嘱》,写一篇数学感想。
指数函数
复习回顾
计算:
(1)
(2)
(3)
(4)
(5)
一张纸对折1次可得2张,对折2次可得4张…,请写出对折x次可得张数y与x的函数关系式。若能将这张厚约0.1mm的纸,对折30次,你敢从上面跳下来吗?
一根长度为1的木棒,第一次截去棒长的一半,第二次再截去剩余木棒的一半,……,截了x 次后木棒剩下的长度是 y,试写出y 与x 之间的关系.
一尺之棰,日取其半,万世不竭 。
出自《庄子 天下篇》
一般地,函数 叫指数函数,其中 x 是自变量.函数的定义域是R.
指数函数概念
思考:为何规定a 0,且a 1
判断下列哪些函数是指数函数?
√
×
×
×
×
√
√
×
0
1
1
0
1
1
0
1
1
0
1
0
1
图
象
性
质
(1)定义域:
(2)值域:
(3)过点:
(4)
(4)
(5) (5)
a>1
0
y
x
0
y=ax
(a>1)
当x>0或x<0时,
y的取值范围?
是 R 上的减函数
是 R 上的增函数
即 x = 0 时, y = 1 .
指数函数图象与性质
R
(0,+ ∞ )
当x>0或x<0时,
y的取值范围?
(0,1)
y=ax
(0
0
y
当x>0时, 0< y<1
当x>0时, y>1
当x<0时, 0
单调性
单调性
( 0 , 1 )
(0,1)
y=1
(0,1)
(0,1)
1.利用函数单调性比较下列各题中两个值的大小
指数函数例题
(2)
(3)
(1)
<
(1)
指数函数例题
解:考察指数函数 y=1.7x.
又∵指数2.5<3.
∴y=1.7x 是R上的增函数.
∵底数1.7 > 1
∴1.72.5<1.73.
(2)
<
指数函数例题
解:考察指数函数 y=0.8x.
又∵指数-0.1>-0.2.
∴y=0.8x 是R上的减函数.
∵底数 0 < 0.8 < 1
∴0.8-0.1<0.8-0.2.
>
(3)
指数函数例题
解:根据指数函数的性质,得:
且
从而有
(2)0.75-0.1 0.750.1 ;
指数函数练习
用“>”,“<”填空。
(1)30.8 30.7 ;
>
>
<
(3)2.3-1 0.8-0.5 .
(6)若am
(4)若2m<2n,则m n;
<
>
当0
>
<
通过本节的学习,你对指数函数有什么认识?
指数函数
定义
数形结合
图像
性质
知识小结
指数函数练习
1. 设 ,则( )
A y3>y1>y2 B y2>y1>y3
C y1>y2>y3 D y1>y3>y2
2.函数y=ax-1 -3(a>0且a≠1)必过点 .
3.函数y=(a-1)x在R上是减函数,则a的取值范围是( )
4.已知 ,则a的取值范围是 ( )
C
D
A
5. 函数y=(3a-1)x为指数函数,则 .
学习的秘密在于
勤动脑
勤动手
作业:
(1)习题3-3 A组 4.(2),(4)
B组 3
(2)阅读课本111页C组第2题《富兰克林的遗嘱》,写一篇数学感想。
