2021秋北师版九上数学4.2平行线分线段成比例导学案(有答案)
文档属性
| 名称 | 2021秋北师版九上数学4.2平行线分线段成比例导学案(有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 00:00:00 | ||
图片预览


文档简介
2021秋北师版九上数学4.2平行线分线段成比例导学案
学习目标
1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用.
2.通过运用,能灵活应用性质及推论。
学习策略
1.在授课过程中要根据学生的个体差异,注意因材施教、分层教学,在教学中结合课本“想一想”、“议一议”、“做一做”等教学环节调动学生的潜能,为每一位学生创设施展才能的空间,让学生学得轻松、愉快,培养学生的成就感,使每一位学生都能获得不同程度的成功。
2. 把学生的活动贯穿于教学的整体过程中,提供学生学习合作、交流、探索、归纳的机会,使学生最大限度的动手、动口、动脑、同伴互助,让学生通过实际感悟平行线分线段成比例定理及其推论的区别与联系。
学习过程
一. 复习回顾:
(1)什么叫比例线段?
答:四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
(2)比例的基本性质?
答:如果 a:b =c:d ,那么ad =bc.
如果 ad =bc,那么 a:b =c:d .
如果 a:b =c:d,那么(a-b):b =(c-d):d; (a+b):b =(c+d):d.
二.新课学习:
导读:内容:如图(1)小方格的边长都是1,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。
计算的比值,你有什么发现?
将b向下平移到如下图2的位置,直线m,n与直线b的交点分别为A2,B2 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢?
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
归纳:平行线分线段成比例定理:__________________________________________________.
结合上图思考:
1如何理解“对应线段”?_______________________________________________.
2.平行线分线段成比例定理用符号语言表示为:________________________
平行线分线段定理推论:
导读:内容:如下图,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。过点A1作直线n的平行线,分别交直线b,c于点C2,C3。(如图4 ),图4中有哪些成比例线段?
(图3) (图4)
推论:_____________________________________.
例1 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7 ,EB=5,FC=4.那么AF的长是多少?
(2)如果AB=10 ,AE=6,AF=5.那么FC的长是多少?
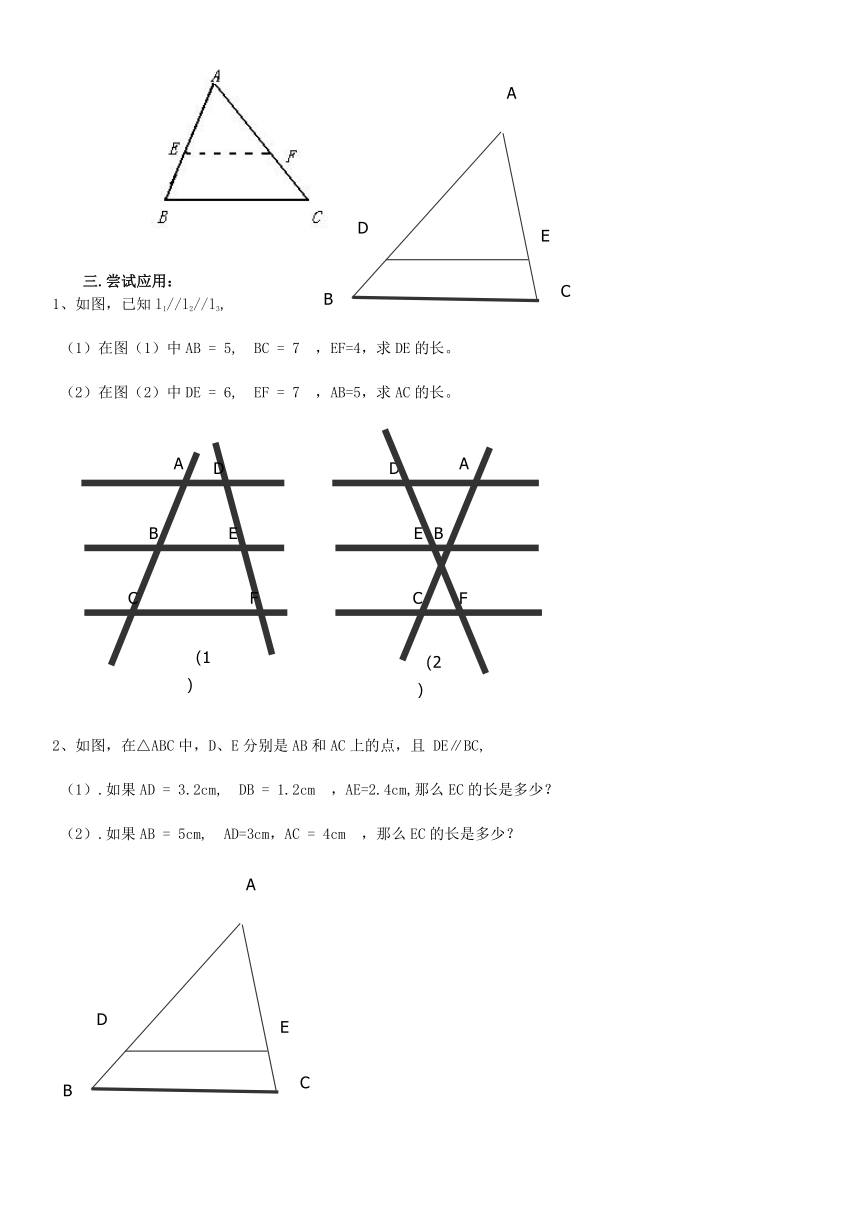
三.尝试应用:
1、如图,已知l1//l2//l3,
(1)在图(1)中AB = 5, BC = 7 ,EF=4,求DE的长。
(2)在图(2)中DE = 6, EF = 7 ,AB=5,求AC的长。
2、如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥BC,
(1).如果AD = 3.2cm, DB = 1.2cm ,AE=2.4cm,那么EC的长是多少?
(2).如果AB = 5cm, AD=3cm,AC = 4cm ,那么EC的长是多少?
四.自主总结:
1平行线分线段成比例定理:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
五.达标测试
一、选择题
1.如图,在△ABC中,DE∥BC,若=,则=( )
A. B. C. D.
2.如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )
A. B. C. D.
二、填空题:
3如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则= .
4.如图,顽皮的小聪在小芳的作业本上用红笔画了个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),A、B、C、D、O都在横格线上,且AD、BC为线段.若线段BO=4cm,则线段BC=
cm.
5. 如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD= .
6. 如图,AD为△ABC的中线,AE=AD,BE交AC于点F,DH∥BF,则= .
三、解答题:
7. 如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
8. 如图,四边形ABCD中,AB∥CD,E为AD的中点,若EF∥AB.求证:BF=CF
达标测试答案:
一.选择题
1.C.
2. D.
二.填空题
3. .
4. 10.
5. 4.5.
6. .
三.解答题
7.解:∵l2∥l3,∴=,
而AG=4,AB=2BC,∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
8.证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G,
∵AH∥EF∥DG,AD∥GH,
∴四边形AHFE和四边形DEFG都是平行四边形,
∴FH=AE,FG=DE,
∵AE=DE,
∴FG=FH,
∵AB∥DG,
∴∠G=∠FHB,∠GCF=∠B,
∴△CFG≌△BFH,
∴FC=FB;
A
B
C
D
E
F
(1)
A
B
C
D
E
F
(2)
A
B
C
D
E
A
B
C
D
E
学习目标
1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用.
2.通过运用,能灵活应用性质及推论。
学习策略
1.在授课过程中要根据学生的个体差异,注意因材施教、分层教学,在教学中结合课本“想一想”、“议一议”、“做一做”等教学环节调动学生的潜能,为每一位学生创设施展才能的空间,让学生学得轻松、愉快,培养学生的成就感,使每一位学生都能获得不同程度的成功。
2. 把学生的活动贯穿于教学的整体过程中,提供学生学习合作、交流、探索、归纳的机会,使学生最大限度的动手、动口、动脑、同伴互助,让学生通过实际感悟平行线分线段成比例定理及其推论的区别与联系。
学习过程
一. 复习回顾:
(1)什么叫比例线段?
答:四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
(2)比例的基本性质?
答:如果 a:b =c:d ,那么ad =bc.
如果 ad =bc,那么 a:b =c:d .
如果 a:b =c:d,那么(a-b):b =(c-d):d; (a+b):b =(c+d):d.
二.新课学习:
导读:内容:如图(1)小方格的边长都是1,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。
计算的比值,你有什么发现?
将b向下平移到如下图2的位置,直线m,n与直线b的交点分别为A2,B2 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢?
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
归纳:平行线分线段成比例定理:__________________________________________________.
结合上图思考:
1如何理解“对应线段”?_______________________________________________.
2.平行线分线段成比例定理用符号语言表示为:________________________
平行线分线段定理推论:
导读:内容:如下图,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。过点A1作直线n的平行线,分别交直线b,c于点C2,C3。(如图4 ),图4中有哪些成比例线段?
(图3) (图4)
推论:_____________________________________.
例1 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7 ,EB=5,FC=4.那么AF的长是多少?
(2)如果AB=10 ,AE=6,AF=5.那么FC的长是多少?
三.尝试应用:
1、如图,已知l1//l2//l3,
(1)在图(1)中AB = 5, BC = 7 ,EF=4,求DE的长。
(2)在图(2)中DE = 6, EF = 7 ,AB=5,求AC的长。
2、如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥BC,
(1).如果AD = 3.2cm, DB = 1.2cm ,AE=2.4cm,那么EC的长是多少?
(2).如果AB = 5cm, AD=3cm,AC = 4cm ,那么EC的长是多少?
四.自主总结:
1平行线分线段成比例定理:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
五.达标测试
一、选择题
1.如图,在△ABC中,DE∥BC,若=,则=( )
A. B. C. D.
2.如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )
A. B. C. D.
二、填空题:
3如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则= .
4.如图,顽皮的小聪在小芳的作业本上用红笔画了个“×”(作业本中的横格线都平行,且相邻两条横格线间的距离都相等),A、B、C、D、O都在横格线上,且AD、BC为线段.若线段BO=4cm,则线段BC=
cm.
5. 如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD= .
6. 如图,AD为△ABC的中线,AE=AD,BE交AC于点F,DH∥BF,则= .
三、解答题:
7. 如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
8. 如图,四边形ABCD中,AB∥CD,E为AD的中点,若EF∥AB.求证:BF=CF
达标测试答案:
一.选择题
1.C.
2. D.
二.填空题
3. .
4. 10.
5. 4.5.
6. .
三.解答题
7.解:∵l2∥l3,∴=,
而AG=4,AB=2BC,∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
8.证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G,
∵AH∥EF∥DG,AD∥GH,
∴四边形AHFE和四边形DEFG都是平行四边形,
∴FH=AE,FG=DE,
∵AE=DE,
∴FG=FH,
∵AB∥DG,
∴∠G=∠FHB,∠GCF=∠B,
∴△CFG≌△BFH,
∴FC=FB;
A
B
C
D
E
F
(1)
A
B
C
D
E
F
(2)
A
B
C
D
E
A
B
C
D
E
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
