2021-2022学年人教版数学八年级上册_ 14.2.1 平方差公式 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册_ 14.2.1 平方差公式 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 851.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 17:30:13 | ||
图片预览





文档简介
(共15张PPT)
乘 法 公 式
平 方 差 公式
情境引入
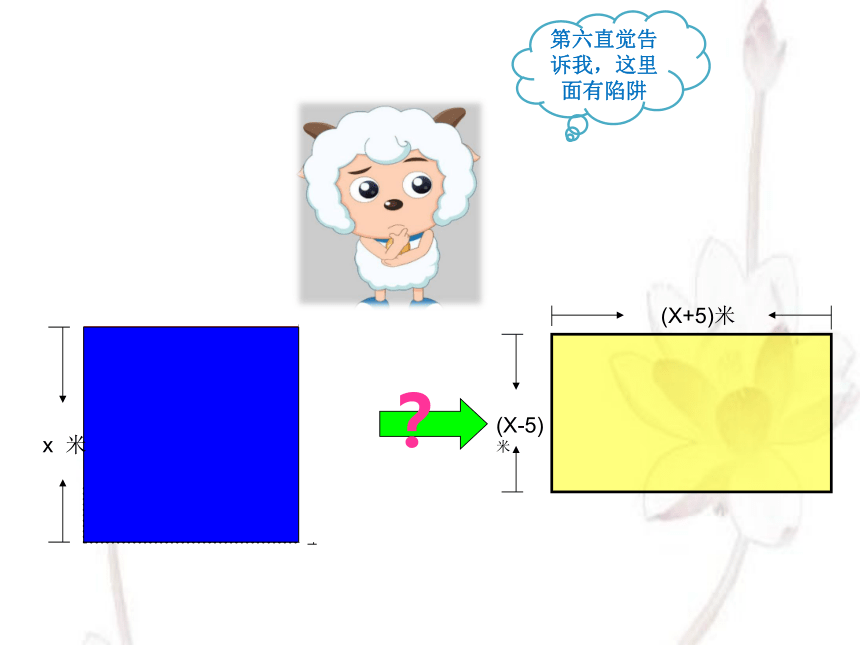
我在您那里预定了一片边长为x米的正方形草地
最近预定的羊羊们太多了。我给你换一个长方形的草地,比原来的一边增加5米,另一边减少5米,这样好看多了,草地面积还一样,你也没有吃亏,你看如何?
懒洋洋
灰太狼
好哒!
懒洋洋
灰太狼
且慢
5米
5米
x 米
(X-5)米
(X+5)米
?
第六直觉告诉我,这里面有陷阱
让村长来给你们上一课吧!
x 米
(X-5)米
(X+5)米
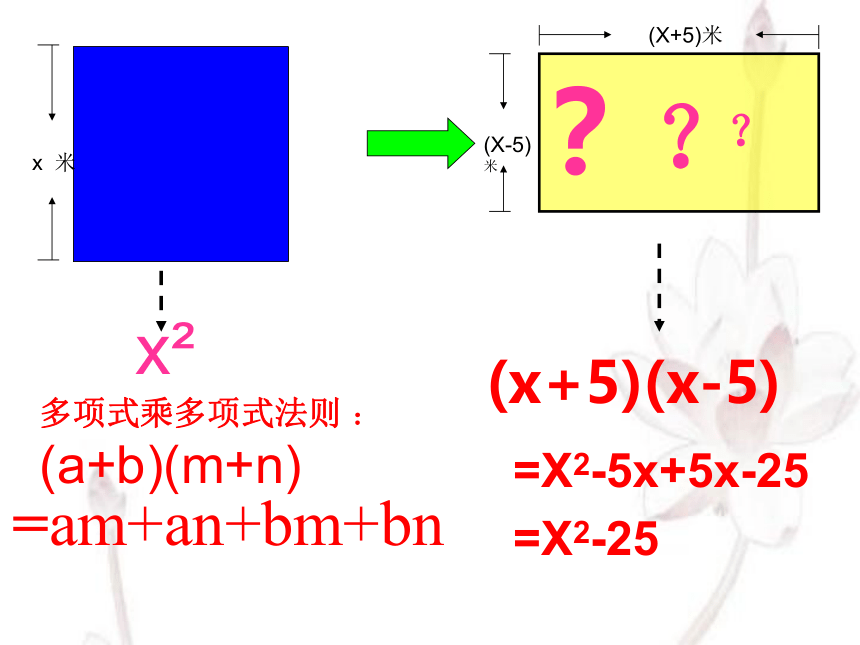
x
(x+5)(x-5)
=X2-5x+5x-25
=X2-25
多项式乘多项式法则 : (a+b)(m+n)
=am+an+bm+bn
?
?
?
探究新课
计算下列多项式X多项式的积,你能发现什么规律?
=
=
=
=
=
=
相同
互为相反数
平方
平方
归纳总结
平方差公式
证明:(a+b)(a-b)
两数和与这两数差的积,等于它们的平方差.
(多项式乘法法则)
(合并同类项)
注:这里的a、b可以是两个单项式,也可以是两个多项式.
即: (a+b)(a-b)
课堂讲解
【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
【解析】 (1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
只有符合(a+b)
(a- b)的形式才能用平方差公式
习题巩固
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
1、下列式子可用平方差公式计算吗 为什么 如果能够,怎样计算
(第一个数不完全一样 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
2、利用平方差公式计算:
原式=(-2y-x)(-2y+x)
= 4y2-x2
原式=(5+2x)(5-2x)
= 25-4x2
原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x
平方差公式的逆用
a2-b2 = (a+b)(a-b)
【解析】
3、计算:
(1) 102×98;
(2) (y+2)(y-2)–(y-1)(y+5) .
解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
这两个数字如何变化,能够利用平方差公式呢?
2、先化简,再求值。【其中a=-1,b=1 】
3、先化简,再求值。【其中 】
4、先化简,再求值。【其中 】
能力提升
1、已知x2-y2=8,x-y=4,求x+y的值。
课堂小结
今天我们主要学习了什么呢?
1、经历探索平方差公式的过程,会推导平方差公式;
2、理解平方差公式的结构特征,灵活应用平方差公式.
乘 法 公 式
平 方 差 公式
情境引入
我在您那里预定了一片边长为x米的正方形草地
最近预定的羊羊们太多了。我给你换一个长方形的草地,比原来的一边增加5米,另一边减少5米,这样好看多了,草地面积还一样,你也没有吃亏,你看如何?
懒洋洋
灰太狼
好哒!
懒洋洋
灰太狼
且慢
5米
5米
x 米
(X-5)米
(X+5)米
?
第六直觉告诉我,这里面有陷阱
让村长来给你们上一课吧!
x 米
(X-5)米
(X+5)米
x
(x+5)(x-5)
=X2-5x+5x-25
=X2-25
多项式乘多项式法则 : (a+b)(m+n)
=am+an+bm+bn
?
?
?
探究新课
计算下列多项式X多项式的积,你能发现什么规律?
=
=
=
=
=
=
相同
互为相反数
平方
平方
归纳总结
平方差公式
证明:(a+b)(a-b)
两数和与这两数差的积,等于它们的平方差.
(多项式乘法法则)
(合并同类项)
注:这里的a、b可以是两个单项式,也可以是两个多项式.
即: (a+b)(a-b)
课堂讲解
【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
【解析】 (1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
只有符合(a+b)
(a- b)的形式才能用平方差公式
习题巩固
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
1、下列式子可用平方差公式计算吗 为什么 如果能够,怎样计算
(第一个数不完全一样 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
2、利用平方差公式计算:
原式=(-2y-x)(-2y+x)
= 4y2-x2
原式=(5+2x)(5-2x)
= 25-4x2
原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x
平方差公式的逆用
a2-b2 = (a+b)(a-b)
【解析】
3、计算:
(1) 102×98;
(2) (y+2)(y-2)–(y-1)(y+5) .
解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
这两个数字如何变化,能够利用平方差公式呢?
2、先化简,再求值。【其中a=-1,b=1 】
3、先化简,再求值。【其中 】
4、先化简,再求值。【其中 】
能力提升
1、已知x2-y2=8,x-y=4,求x+y的值。
课堂小结
今天我们主要学习了什么呢?
1、经历探索平方差公式的过程,会推导平方差公式;
2、理解平方差公式的结构特征,灵活应用平方差公式.
