2020--2021学年北师大版九年级数学下册 _3.2 圆的对称性 课件(共18张PPT)
文档属性
| 名称 | 2020--2021学年北师大版九年级数学下册 _3.2 圆的对称性 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 17:51:09 | ||
图片预览






文档简介
(共18张PPT)
3.2 圆的对称性
创设情境 温故探新
复习
导入
1.圆的两要素是_______、________,它们分别决定圆的________、__________.
2.下列3种图形:①等边三角形;②平行四边形;③矩形,既是轴对称图形,又是中心对称图形的是(填序号):________________.
合作交流探究新知
自主探究
1.自读教材P70—72的内容思考如下问题:
(1)请同学们拿出准备好的圆形纸片,你知道圆有哪些基本性质吗?
(2)圆是轴对称图形吗?如果是,它的对称轴是什么?你是怎么得到的?
(3)圆是中心对称图形吗?如果是,它的对称中心是什么?你是怎么得到的?
合作交流探究新知
自主探究
轴对称性:圆是轴对称图形,其对称轴是任意一条过圆心的直线.
旋转不变性:一个圆绕着它的圆心旋转任意一个角度,都能与圆来的图形重合.
中心对称性:圆是中心对称图形,对称中心为圆心.
合作交流探究新知
自主探究
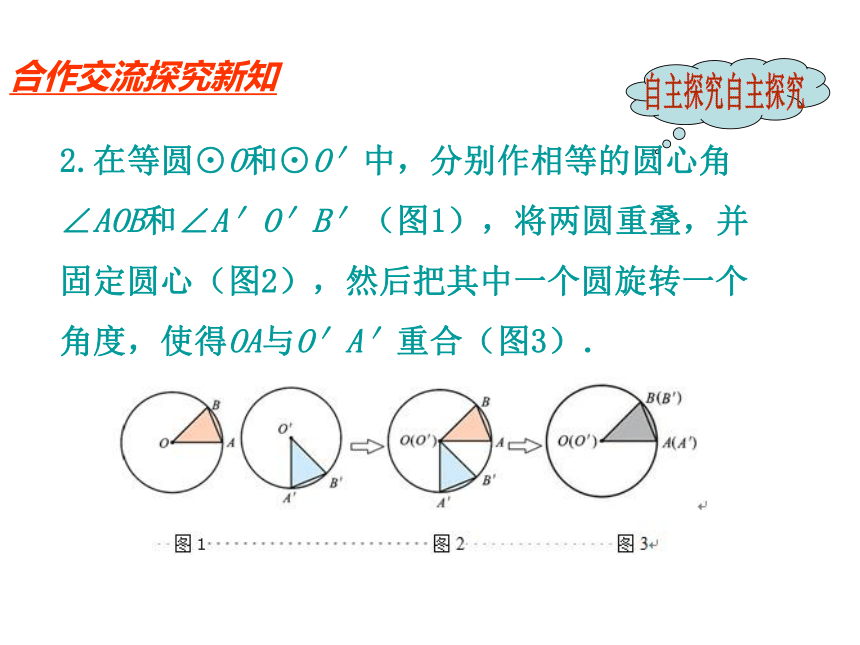
2.在等圆⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′(图1),将两圆重叠,并固定圆心(图2),然后把其中一个圆旋转一个角度,使得OA与O′A′重合(图3).
合作交流探究新知
自主探究
(1)通过操作,对比图1和图3,你能发现哪些等量关系?
(2)你得到这些等量关系的理由是什么?
(3)由此你能得到什么结论?
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
合作交流探究新知
自主探究
3. 思考上述命题的逆命题是否成立,发散思维拓展新定理.
(1)在同圆或等圆中,如果两个圆心角所对的弧相等,这两个圆心角相等吗?那么它们所的对的弦相等吗?你是怎么想的?
(2)在同圆或等圆中,如果两条弦相等,你能得出什么结论?
(3)一条弦所对的弧有几条?
(4)上面的命题怎样叙述能够更准确?
(5)观察以上所得出的结论,你能将其总结为一条定理吗?
合作交流探究新知
自主探究
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
范例研讨运用新知
自主探究
例:如图,AB,DE是⊙O的直径,C是⊙O上的一点,且 ,BE与CE的大小有什么关系?为什么?
范例研讨运用新知
自主探究
1.∠AOD和∠BOE的度数有什么数量关系?
2.根据角的数量关系可以得到哪两条弧相等?
3.根据已知条件如何转化弧的等量关系?
4.根据弧之间的关系你能得到正确的结论吗?
5.试着合作完成证明过程.
范例研讨运用新知
自主探究
解:
BE=CE.理由是:
∵∠AOD=∠BOE
∴
又∵
∴
∴
1. 下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
反馈练习巩固新知
你一定能行!
D
反馈练习巩固新知
你一定能行!
2. 下列叙述不正确的是 .①圆既是轴对称图形,又是中心对称图形;②圆有无数条对称轴,任何一条直径都是它的对称轴;③相等的弦所对的弧相等;④等弧所对的弦相等.
①④
反馈练习巩固新知
你一定能行!
3. (2015秋 官渡区期末)如图,在⊙O中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
反馈练习巩固新知
你一定能行!
证明:∵ ,
∴AB=AC
∴△ABC是等腰三角形
∵∠ACB=60°
∴△ABC是等边三角形,
∴AB=BC=CA
∴∠AOB=∠BOC=∠COA.
课堂小结布置作业
小结:
今天你有哪些收获
1.圆是轴对称图形,其对称轴是任意一条过圆心的直线.
2.圆是中心对称图形,对称中心是圆心.
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
4.在同圆或等圆中,如果两个圆心角、两条弧,两条弦中有一组量相等,那么它们所对应的其余各足量都分别相等.
课堂小结布置作业
作业:
1.课本第72页随堂练习第1、2、3题.
2.课本第72-73页习题3.2第1、2、3题.
谢谢指导
再见
3.2 圆的对称性
创设情境 温故探新
复习
导入
1.圆的两要素是_______、________,它们分别决定圆的________、__________.
2.下列3种图形:①等边三角形;②平行四边形;③矩形,既是轴对称图形,又是中心对称图形的是(填序号):________________.
合作交流探究新知
自主探究
1.自读教材P70—72的内容思考如下问题:
(1)请同学们拿出准备好的圆形纸片,你知道圆有哪些基本性质吗?
(2)圆是轴对称图形吗?如果是,它的对称轴是什么?你是怎么得到的?
(3)圆是中心对称图形吗?如果是,它的对称中心是什么?你是怎么得到的?
合作交流探究新知
自主探究
轴对称性:圆是轴对称图形,其对称轴是任意一条过圆心的直线.
旋转不变性:一个圆绕着它的圆心旋转任意一个角度,都能与圆来的图形重合.
中心对称性:圆是中心对称图形,对称中心为圆心.
合作交流探究新知
自主探究
2.在等圆⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′(图1),将两圆重叠,并固定圆心(图2),然后把其中一个圆旋转一个角度,使得OA与O′A′重合(图3).
合作交流探究新知
自主探究
(1)通过操作,对比图1和图3,你能发现哪些等量关系?
(2)你得到这些等量关系的理由是什么?
(3)由此你能得到什么结论?
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
合作交流探究新知
自主探究
3. 思考上述命题的逆命题是否成立,发散思维拓展新定理.
(1)在同圆或等圆中,如果两个圆心角所对的弧相等,这两个圆心角相等吗?那么它们所的对的弦相等吗?你是怎么想的?
(2)在同圆或等圆中,如果两条弦相等,你能得出什么结论?
(3)一条弦所对的弧有几条?
(4)上面的命题怎样叙述能够更准确?
(5)观察以上所得出的结论,你能将其总结为一条定理吗?
合作交流探究新知
自主探究
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
范例研讨运用新知
自主探究
例:如图,AB,DE是⊙O的直径,C是⊙O上的一点,且 ,BE与CE的大小有什么关系?为什么?
范例研讨运用新知
自主探究
1.∠AOD和∠BOE的度数有什么数量关系?
2.根据角的数量关系可以得到哪两条弧相等?
3.根据已知条件如何转化弧的等量关系?
4.根据弧之间的关系你能得到正确的结论吗?
5.试着合作完成证明过程.
范例研讨运用新知
自主探究
解:
BE=CE.理由是:
∵∠AOD=∠BOE
∴
又∵
∴
∴
1. 下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
反馈练习巩固新知
你一定能行!
D
反馈练习巩固新知
你一定能行!
2. 下列叙述不正确的是 .①圆既是轴对称图形,又是中心对称图形;②圆有无数条对称轴,任何一条直径都是它的对称轴;③相等的弦所对的弧相等;④等弧所对的弦相等.
①④
反馈练习巩固新知
你一定能行!
3. (2015秋 官渡区期末)如图,在⊙O中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
反馈练习巩固新知
你一定能行!
证明:∵ ,
∴AB=AC
∴△ABC是等腰三角形
∵∠ACB=60°
∴△ABC是等边三角形,
∴AB=BC=CA
∴∠AOB=∠BOC=∠COA.
课堂小结布置作业
小结:
今天你有哪些收获
1.圆是轴对称图形,其对称轴是任意一条过圆心的直线.
2.圆是中心对称图形,对称中心是圆心.
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
4.在同圆或等圆中,如果两个圆心角、两条弧,两条弦中有一组量相等,那么它们所对应的其余各足量都分别相等.
课堂小结布置作业
作业:
1.课本第72页随堂练习第1、2、3题.
2.课本第72-73页习题3.2第1、2、3题.
谢谢指导
再见
