第二章 轴对称图形复习题 课件 2021-2022学年苏科版数学八年级上册(共25张PPT)
文档属性
| 名称 | 第二章 轴对称图形复习题 课件 2021-2022学年苏科版数学八年级上册(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 664.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 17:53:54 | ||
图片预览






文档简介
(共25张PPT)
2021
轴对称图形复习
八年级上册
复习回顾
1
1.轴对称的概念:__________
轴对称图形的概念:__________
轴对称与轴对称图形的关系:________
2.轴对称的性质:__________
练习:
下列语句中,正确的有 ( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A.1个 B.2个 C.3个 D.4个
3.线段的对称轴是: __________
线段垂直平分线的定理及逆定理:__________
4.角的对称轴是: __________
角的平分线平分线的定理及逆定理:__________
练习:
1、在△ABC中,AB=AC,OB=OC,且点A到BC的距离为8,点O到BC的距离为3,则AO的长为_______.
2、如图,在△ABC中,∠C=90°,AD平分∠BAC。若CD=6,则点D到AB的距离是_______.
5.等腰三角形的对称轴是: ;
等腰三角形的性质:__________
等腰三角形的判定__________
等边三角形的性质及判定:__________
练习:
1、等腰三角形一腰上的高与底边的夹角为30°,则顶角为_______.
2、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角为_______.
3、等腰三角形一腰垂直平分线与另一腰所在直线相交所得锐角为50°,则顶角为_____.
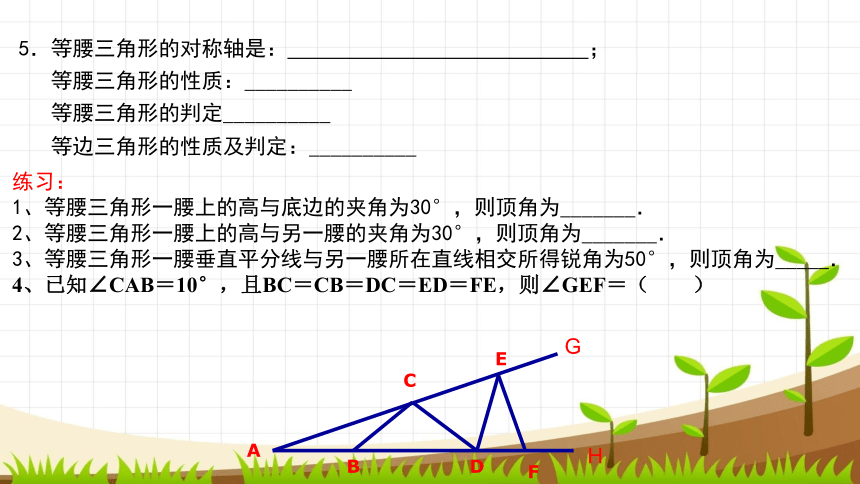
4、已知∠CAB=10°,且BC=CB=DC=ED=FE,则∠GEF=( )
A
B
C
D
E
F
G
H
6.直角三角形的相关性质(涉及斜边中线): ;
直角三角形的相关性质(涉及30度角):________
练习:
若直角三角形斜边上的高和中线长分别是5 cm,6 cm,则它的面积是________.
课堂练习
3
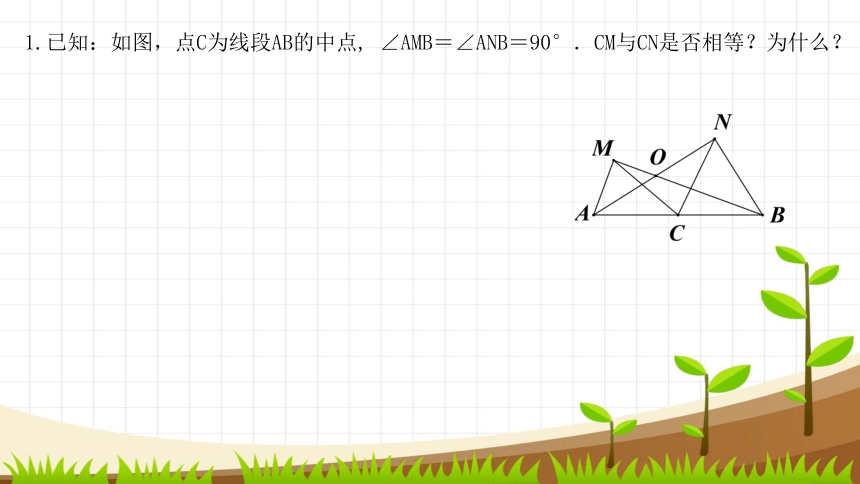
1.已知:如图,点C为线段AB的中点, ∠AMB=∠ANB=90°.CM与CN是否相等?为什么?
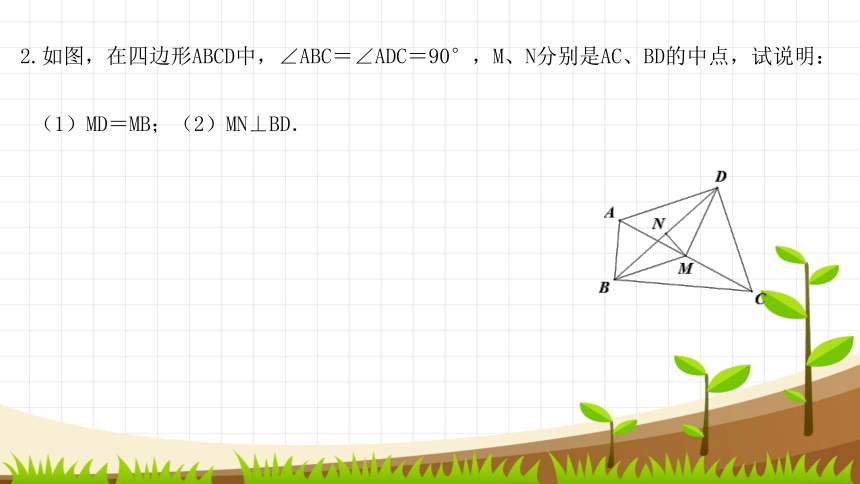
2.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,试说明:
(1)MD=MB;(2)MN⊥BD.
3.尺规作图(保留作图痕迹):如图,已知直线l及其两侧的两点A、B.
(1)在直线l上求一点O,使到A、B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB;
4.在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图1).度量PE、PF的长度,这两条线段相等吗
在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(2)把三角尺绕点P旋转(如图2),PE与PF相等吗 请说明理由.
在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(3)探究:画∠AOB=50°并画/AOB的平分线OC,在OC上任取一点P,作∠EPF=130°∠EPF的两边分别与OA、OB相交于E、F两点(如图3),PE与PF相等吗 请说明理由.
5.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N.
(1)求证:AE=BD;
(2)求证:CM=CN;
(3)连结MN,求证:△CMN是等边三角形;
(4)AE与BD所夹的锐角为 度.
6.如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形 猜想:EF与BE CF之间有怎样的关系,并说明理由
如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(2)如图2,若AB≠AC,其他条件不变,图中还有等腰三角形吗 如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗
如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(3)如图3,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交 AB于E,交AC于F.这时图中还有等腰三角形吗 EF与BE、CF关系又如何 说明你的理由
7.如图,△ABC为等腰直角三角形,∠A=90°, BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证:①BF=BC
7.如图,△ABC为等腰直角三角形,∠A=90°, BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证: ②BD=2CE
8.如图,AB= AC=AD
(1)如果ADIIBC,那么∠C和∠D有怎样的数量关系 证明你的结论;
如图,AB= AC=AD
(2)如果∠C=2∠D,那么你能得到什么结论 证明你的结论.
9.请完成以下题目
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC延长线上,且CE=CA,求∠DAE的度数.
(2)如果把第(1)题中“AB= AC”的条件舍去,其余条件不变,那么∠DAE的度数会改变吗
(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系
课堂小结
4
课堂小结
1、知识点的理解与运用;
2、解题方法的选用;
3、数学思想的渗透:分类与转化
谢谢!
2021
轴对称图形复习
八年级上册
复习回顾
1
1.轴对称的概念:__________
轴对称图形的概念:__________
轴对称与轴对称图形的关系:________
2.轴对称的性质:__________
练习:
下列语句中,正确的有 ( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A.1个 B.2个 C.3个 D.4个
3.线段的对称轴是: __________
线段垂直平分线的定理及逆定理:__________
4.角的对称轴是: __________
角的平分线平分线的定理及逆定理:__________
练习:
1、在△ABC中,AB=AC,OB=OC,且点A到BC的距离为8,点O到BC的距离为3,则AO的长为_______.
2、如图,在△ABC中,∠C=90°,AD平分∠BAC。若CD=6,则点D到AB的距离是_______.
5.等腰三角形的对称轴是: ;
等腰三角形的性质:__________
等腰三角形的判定__________
等边三角形的性质及判定:__________
练习:
1、等腰三角形一腰上的高与底边的夹角为30°,则顶角为_______.
2、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角为_______.
3、等腰三角形一腰垂直平分线与另一腰所在直线相交所得锐角为50°,则顶角为_____.
4、已知∠CAB=10°,且BC=CB=DC=ED=FE,则∠GEF=( )
A
B
C
D
E
F
G
H
6.直角三角形的相关性质(涉及斜边中线): ;
直角三角形的相关性质(涉及30度角):________
练习:
若直角三角形斜边上的高和中线长分别是5 cm,6 cm,则它的面积是________.
课堂练习
3
1.已知:如图,点C为线段AB的中点, ∠AMB=∠ANB=90°.CM与CN是否相等?为什么?
2.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,试说明:
(1)MD=MB;(2)MN⊥BD.
3.尺规作图(保留作图痕迹):如图,已知直线l及其两侧的两点A、B.
(1)在直线l上求一点O,使到A、B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB;
4.在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图1).度量PE、PF的长度,这两条线段相等吗
在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(2)把三角尺绕点P旋转(如图2),PE与PF相等吗 请说明理由.
在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
(3)探究:画∠AOB=50°并画/AOB的平分线OC,在OC上任取一点P,作∠EPF=130°∠EPF的两边分别与OA、OB相交于E、F两点(如图3),PE与PF相等吗 请说明理由.
5.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N.
(1)求证:AE=BD;
(2)求证:CM=CN;
(3)连结MN,求证:△CMN是等边三角形;
(4)AE与BD所夹的锐角为 度.
6.如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形 猜想:EF与BE CF之间有怎样的关系,并说明理由
如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(2)如图2,若AB≠AC,其他条件不变,图中还有等腰三角形吗 如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗
如图1,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(3)如图3,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交 AB于E,交AC于F.这时图中还有等腰三角形吗 EF与BE、CF关系又如何 说明你的理由
7.如图,△ABC为等腰直角三角形,∠A=90°, BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证:①BF=BC
7.如图,△ABC为等腰直角三角形,∠A=90°, BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证: ②BD=2CE
8.如图,AB= AC=AD
(1)如果ADIIBC,那么∠C和∠D有怎样的数量关系 证明你的结论;
如图,AB= AC=AD
(2)如果∠C=2∠D,那么你能得到什么结论 证明你的结论.
9.请完成以下题目
(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC延长线上,且CE=CA,求∠DAE的度数.
(2)如果把第(1)题中“AB= AC”的条件舍去,其余条件不变,那么∠DAE的度数会改变吗
(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系
课堂小结
4
课堂小结
1、知识点的理解与运用;
2、解题方法的选用;
3、数学思想的渗透:分类与转化
谢谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
