华东师大版七上数学 4.6.2角的比较和运算 课件(共29张PPT)
文档属性
| 名称 | 华东师大版七上数学 4.6.2角的比较和运算 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 19:16:36 | ||
图片预览





文档简介
(共29张PPT)
B点
如图,点A、B、C表示足球比赛中3个不同的射门位置。你觉得哪一点射门最容易射进?为什么?
C点
A点
B点,因为射门角越大,则进球机会越大。
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
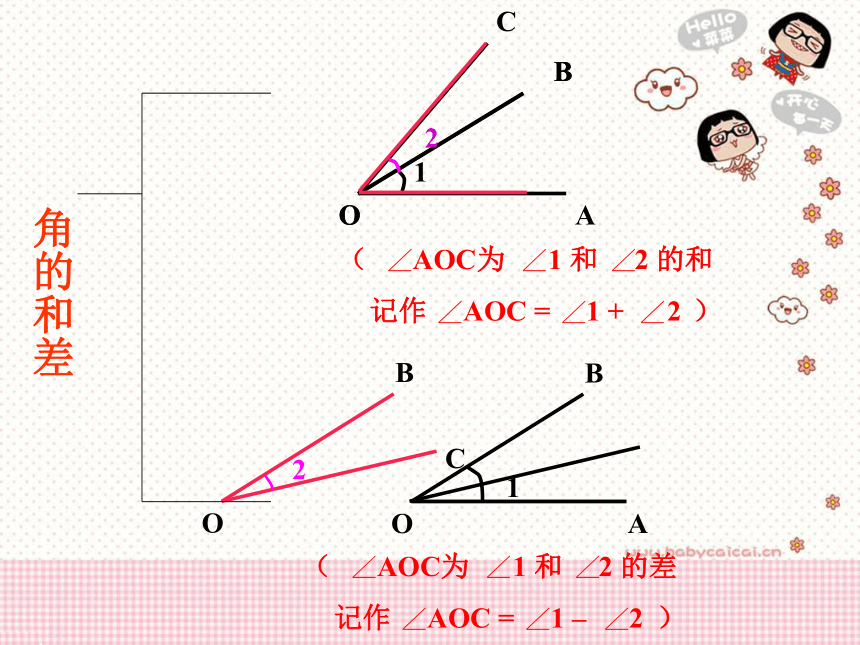
AOC为 1 和 2 的和
记作 AOC = 1 + 2
(
)
AOC为 1 和 2 的差
记作 AOC = 1 – 2
(
)
角的和差
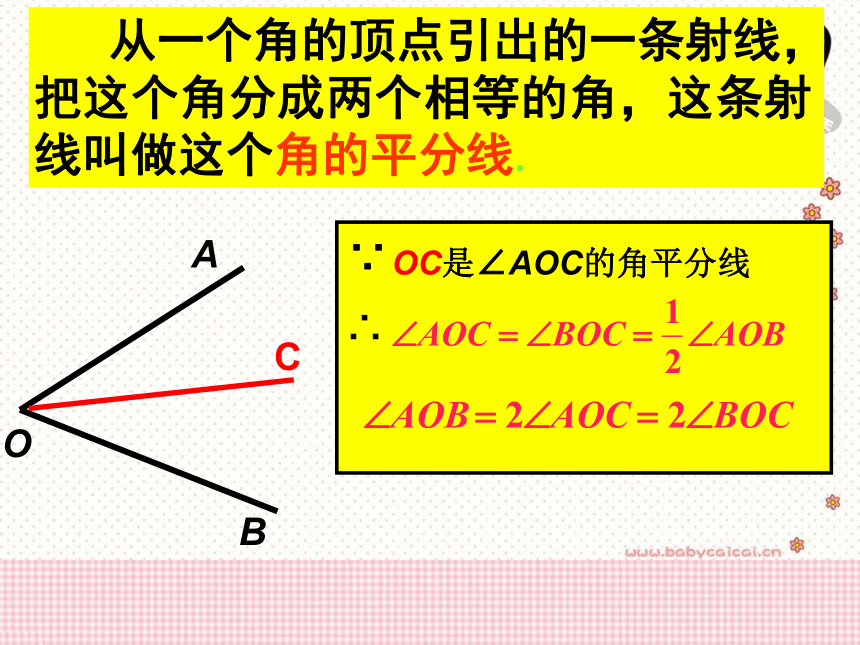
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
A
O
B
C
OC是∠AOC的角平分线
∵
∴
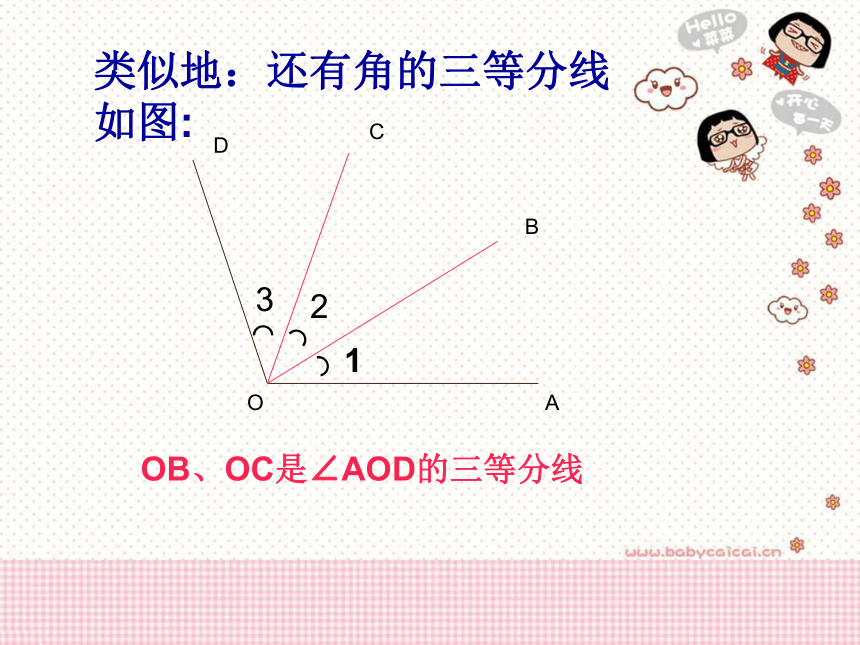
类似地:还有角的三等分线
如图:
O
A
B
C
D
⌒
⌒
⌒
1
2
3
OB、OC是∠AOD的三等分线
例3、加减法计算
解:(1)原式=(12+45)0+(36+24)/+(56+35)//
=570+60/+91//
=570+61/+31//
=580+1/+31//
=5801/31//
题型二:角度的加减法运算
(1) 12036/56// + 45024/35//
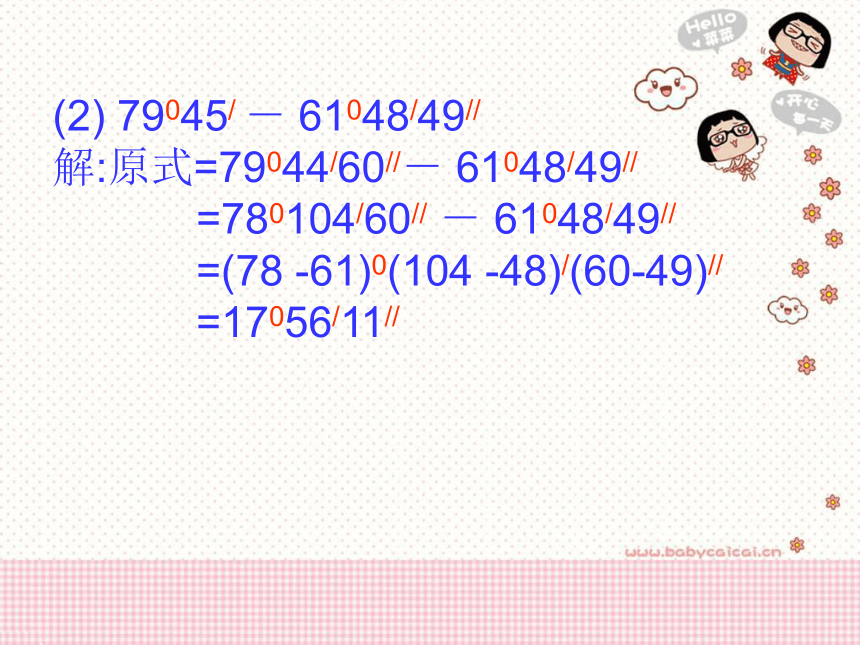
(2) 79045/ - 61048/49//
(2) 79045/ - 61048/49//
解:原式=79044/60//- 61048/49//
=780104/60// - 61048/49//
=(78 -61)0(104 -48)/(60-49)//
=17056/11//
例5:计算
例题讲解
=82°59′36″
解(1)
=37°38′+45°21.6′
= 37°38′+45°21′36″
解
=32°36′
=46°60′-14°24′
=(46-14)°(60-24)′
=(37+45)°(38+21)′36″
例4、乘除法运算
(3)21031/27//×3 (4) 63021/39//÷3
(5)10606/25//÷5
解:原式=(21×3)0(31×3)/(27×3)//
=63093/81//
=63094/21//
=64034/21//
题型三:角度的乘除法运算
(4) 63021/39//÷3
解:原式=(63÷3)0(21÷3)/(39÷3)//
=2107/13//
(5)10606/25//÷5
解:原式=(106÷5)0(6÷5)/(25÷5)//
=210(66÷5)/ (25÷5)//
=21013/(85÷5)//
=21013/17//
题型三:角度的乘除法运算
角的和差填空:
(1)∠AOB =( )+( )+( )
(2)∠BOC=( )+ ( )
(3)∠AOD=( )+ ( )
(4)∠AOB-∠AOC = ( )
(5)∠COD= ∠AOD-( )
= ∠BOC-( )
(6)∠BOD=( ) - ( )-( )
∠AOC
∠COD
∠BOD
看谁填的准!
C
B
O
A
D
∠COD
∠BOD
∠AOC
∠COD
∠BOC
∠AOC
∠BOD
∠AOB
∠AOC
∠COD
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1) ∠D0B ∠BOC
2) ∠C0B ∠AOC
3) ∠DOC+∠COB ∠B0D
>
<
=
同类练习1:
A
B
D
C
( 1 ) ∠DAB = ∠DAC+∠
( 2 ) ∠ACB =∠DCB –
CAB
∠DCA
( 1 )∠ABC = ∠ABD ∠CBD
( 2 )∠BDC = ∠ADC ∠BDA
+
–
A
B
D
C
考考你?
C
B
O
A
图(1)
2、如图(2)若∠AOC=90°, ∠BOD=90°那么
图中相等的角是 。
D
C
B
O
A
图(2)
看图填空:
1、如图(1)若∠AOC=32°,∠BOC=43°则
∠AOB= 。 若已知 ∠AOB = 68 ° ∠BOC=40°则∠AOC= 。
75 °
28°
∠AOB= ∠COD
∠AOC= ∠BOD
如图,OB是∠AOC的平分线,OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
例:如图O是直线AB上一点, ∠AOC=53°17′∠BOC度数
A
O
B
C
分析:(1) AB是直线 , ∠AOB 是什么角
(2)∠BOC 、 ∠AOB 、 ∠AOC之间有什么关系
(∠AOB是平角,等于180°)
∠AOB = ∠BOC + ∠AOC
解: ∠BOC= ∠AOB- ∠AOC=180°- 53°17′
=126°43′
例题讲解
已知O为直线AB上一点,OE平分∠AOC,
OF平分 ∠COB,求∠EOF的大小?
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
= ∠AOC+ ∠COB
= (∠AOC+∠COB)
=90 °
∴∠EOC= ∠AOC,
∠COF= ∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
A
O
B
C
D
已知:OC平分 ∠AOB,
∠AOB=1000,OD平分∠AOC
求:∠COD的度数
O
A
B
C
D
已知:∠AOD=320,∠BOD=1080
OC平分∠AOB
求: ∠COD的度数。
如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°
∴∠AOB=1/3∠AOD=38°
∵OC平分∠AOD
∴∠AOC=1/2∠AOD=57°
(角平分线的定义)
∴∠BOC=∠AOC-∠AOB
(角的和差关系)
∠BOD=2∠AOB
=57°-38°
=19°(角的和差关系)
A
B
D
C
A
B
D
C
3.已知 OB是∠AOC的平分线,OD是∠COE的平分线。
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?
30°
30°
40°
40°
已知:如图∠AOC= ∠BOD=90°,
∠BOC=40°,求 ∠AOD=
解:
∴ ∠AOD= ∠AOB+ ∠BOC+ ∠COD=140°
∵∠AOC=90°,∠BOC=40°
∴ ∠AOB=50°
又 ∵ ∠BOD=90°, ∠BOC=40°
∴ ∠COD=50°
50°
50°
40°
O
C
A
D
B
2. 如图, ∠AOC =40 ° , ∠COB=70°, ON、OM分别 平 分∠AOC 、∠COB, 求: ∠MON的度数.
N
C
M
B
O
A
解:∵ ON平分∠AOC ,
∴ ∠NOC = 1/2 ∠AOC =20°,
∵OM平分 ∠COB,
∴ ∠COM = 1/2 ∠COB= 35°,
=20°+35°
=55°.
20°
35°
∴ ∠MON= ∠NOC + ∠COM
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
则∠AOB+∠DOC= ____.
29
H
X
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
180°
则∠AOB+∠DOC= .
= 90° +90°
= 180°
解: ∠AOB+∠DOC
+ ∠DOC
= 90° +∠DOA + ∠DOC
29
X
= ∠BOD +∠DOA
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
则∠AOB+∠DOC= ____.
29
H
180°
A
B
C
D
O
A
B
C
D
E
B点
如图,点A、B、C表示足球比赛中3个不同的射门位置。你觉得哪一点射门最容易射进?为什么?
C点
A点
B点,因为射门角越大,则进球机会越大。
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
AOC为 1 和 2 的和
记作 AOC = 1 + 2
(
)
AOC为 1 和 2 的差
记作 AOC = 1 – 2
(
)
角的和差
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
A
O
B
C
OC是∠AOC的角平分线
∵
∴
类似地:还有角的三等分线
如图:
O
A
B
C
D
⌒
⌒
⌒
1
2
3
OB、OC是∠AOD的三等分线
例3、加减法计算
解:(1)原式=(12+45)0+(36+24)/+(56+35)//
=570+60/+91//
=570+61/+31//
=580+1/+31//
=5801/31//
题型二:角度的加减法运算
(1) 12036/56// + 45024/35//
(2) 79045/ - 61048/49//
(2) 79045/ - 61048/49//
解:原式=79044/60//- 61048/49//
=780104/60// - 61048/49//
=(78 -61)0(104 -48)/(60-49)//
=17056/11//
例5:计算
例题讲解
=82°59′36″
解(1)
=37°38′+45°21.6′
= 37°38′+45°21′36″
解
=32°36′
=46°60′-14°24′
=(46-14)°(60-24)′
=(37+45)°(38+21)′36″
例4、乘除法运算
(3)21031/27//×3 (4) 63021/39//÷3
(5)10606/25//÷5
解:原式=(21×3)0(31×3)/(27×3)//
=63093/81//
=63094/21//
=64034/21//
题型三:角度的乘除法运算
(4) 63021/39//÷3
解:原式=(63÷3)0(21÷3)/(39÷3)//
=2107/13//
(5)10606/25//÷5
解:原式=(106÷5)0(6÷5)/(25÷5)//
=210(66÷5)/ (25÷5)//
=21013/(85÷5)//
=21013/17//
题型三:角度的乘除法运算
角的和差填空:
(1)∠AOB =( )+( )+( )
(2)∠BOC=( )+ ( )
(3)∠AOD=( )+ ( )
(4)∠AOB-∠AOC = ( )
(5)∠COD= ∠AOD-( )
= ∠BOC-( )
(6)∠BOD=( ) - ( )-( )
∠AOC
∠COD
∠BOD
看谁填的准!
C
B
O
A
D
∠COD
∠BOD
∠AOC
∠COD
∠BOC
∠AOC
∠BOD
∠AOB
∠AOC
∠COD
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1) ∠D0B ∠BOC
2) ∠C0B ∠AOC
3) ∠DOC+∠COB ∠B0D
>
<
=
同类练习1:
A
B
D
C
( 1 ) ∠DAB = ∠DAC+∠
( 2 ) ∠ACB =∠DCB –
CAB
∠DCA
( 1 )∠ABC = ∠ABD ∠CBD
( 2 )∠BDC = ∠ADC ∠BDA
+
–
A
B
D
C
考考你?
C
B
O
A
图(1)
2、如图(2)若∠AOC=90°, ∠BOD=90°那么
图中相等的角是 。
D
C
B
O
A
图(2)
看图填空:
1、如图(1)若∠AOC=32°,∠BOC=43°则
∠AOB= 。 若已知 ∠AOB = 68 ° ∠BOC=40°则∠AOC= 。
75 °
28°
∠AOB= ∠COD
∠AOC= ∠BOD
如图,OB是∠AOC的平分线,OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
例:如图O是直线AB上一点, ∠AOC=53°17′∠BOC度数
A
O
B
C
分析:(1) AB是直线 , ∠AOB 是什么角
(2)∠BOC 、 ∠AOB 、 ∠AOC之间有什么关系
(∠AOB是平角,等于180°)
∠AOB = ∠BOC + ∠AOC
解: ∠BOC= ∠AOB- ∠AOC=180°- 53°17′
=126°43′
例题讲解
已知O为直线AB上一点,OE平分∠AOC,
OF平分 ∠COB,求∠EOF的大小?
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
= ∠AOC+ ∠COB
= (∠AOC+∠COB)
=90 °
∴∠EOC= ∠AOC,
∠COF= ∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
A
O
B
C
D
已知:OC平分 ∠AOB,
∠AOB=1000,OD平分∠AOC
求:∠COD的度数
O
A
B
C
D
已知:∠AOD=320,∠BOD=1080
OC平分∠AOB
求: ∠COD的度数。
如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°
∴∠AOB=1/3∠AOD=38°
∵OC平分∠AOD
∴∠AOC=1/2∠AOD=57°
(角平分线的定义)
∴∠BOC=∠AOC-∠AOB
(角的和差关系)
∠BOD=2∠AOB
=57°-38°
=19°(角的和差关系)
A
B
D
C
A
B
D
C
3.已知 OB是∠AOC的平分线,OD是∠COE的平分线。
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?
30°
30°
40°
40°
已知:如图∠AOC= ∠BOD=90°,
∠BOC=40°,求 ∠AOD=
解:
∴ ∠AOD= ∠AOB+ ∠BOC+ ∠COD=140°
∵∠AOC=90°,∠BOC=40°
∴ ∠AOB=50°
又 ∵ ∠BOD=90°, ∠BOC=40°
∴ ∠COD=50°
50°
50°
40°
O
C
A
D
B
2. 如图, ∠AOC =40 ° , ∠COB=70°, ON、OM分别 平 分∠AOC 、∠COB, 求: ∠MON的度数.
N
C
M
B
O
A
解:∵ ON平分∠AOC ,
∴ ∠NOC = 1/2 ∠AOC =20°,
∵OM平分 ∠COB,
∴ ∠COM = 1/2 ∠COB= 35°,
=20°+35°
=55°.
20°
35°
∴ ∠MON= ∠NOC + ∠COM
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
则∠AOB+∠DOC= ____.
29
H
X
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
180°
则∠AOB+∠DOC= .
= 90° +90°
= 180°
解: ∠AOB+∠DOC
+ ∠DOC
= 90° +∠DOA + ∠DOC
29
X
= ∠BOD +∠DOA
┓
┏
3.将一副三角板按图示方法放置(直角顶点重合)
C
O
A
D
B
则∠AOB+∠DOC= ____.
29
H
180°
A
B
C
D
O
A
B
C
D
E
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
