2021-2022学年数学人教A版(2019)必修第一册4.1.1n次方根和分数指数幂教学课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册4.1.1n次方根和分数指数幂教学课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 22:01:49 | ||
图片预览






文档简介
(共18张PPT)
第四章 指数函数对数函数
4.1指数
4.1.1 n次方根与分数指数幂
引入
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现. 这里的巨型城址,面积近360万平方米,包括古城、水坝和多处高等级建筑. 考古学家利用遗址中遗存的碳14的残留量测定,古城存在的时期为公元前3300年~2500年,你知道考古学家测定遗址年代用的是什么数学知识吗?
实际上,考古学家所用的数学知识就是本章即将要学习的指数函数. 指数函数在解决实际问题中有着广泛的应用. 例如,在自然条件下,细胞的分裂、人口的增长、放射性物质的衰减等问题,都可利用指数函数构建数学模型来刻画它们的变化规律。
通过幂函数的学习,我们已经体验了研究一类函数的过程和方法. 在本章,我们将类比幂函数的研究方法,学习指数函数和对数函数的概念、图象和性质,并对这三类基本初等函数的变化规律的差异进行比较,在此基础上,通过解决简单的实际问题,体会如何根据变化差异,选择合适和函数类型构建数学模型,刻画现实问题的变化规律。
本节(4.1指数)要学习的内容和过程大致为
(1)将根式的概念推广到n次方根;
(2)利用n次方根的定义和运算,定义分数指数幂,把幂中
的指数x的范围推广到有理数;
(3)类比从有理数扩充到实数的过程,把有理数指数幂推广
到实数指数幂.
为了研究指数函数,我们需要将指数的范围拓展到全体实数.
初中已经学过整数指数幂,负指数幂、零指数幂,有学习幂
函数时,我们把正方形场地的边长 c关于面积S的函数
知识探究(一)
问题1:初中阶段我们学过平方根、立方根的概念,你能回想出这些概念吗?能举例说明吗?
思考(1): 类比平方根,立方根,你能写出4次方根,5次方根,... ...,n 次方根的规定吗?
一般地,如果xn=a(n∈N*且n>1),那么x叫a的n次方根.
n次方根
思考(2): 任何实数a都一定有n 次方根吗?如何有,有几个呢?请举例说明.
(1)当n是奇数时,
任意实数a都有n次方根,且只有一个. 记作:
(2)当n是偶数时,
①若a>0,则a有n次方根, 且有两个. 记作:
②若a=0,则a有n次方根, 且只有一个0,即
③若a<0,则a的n次方根不存在.
说明:
为什么负数没有偶次方根?
返回
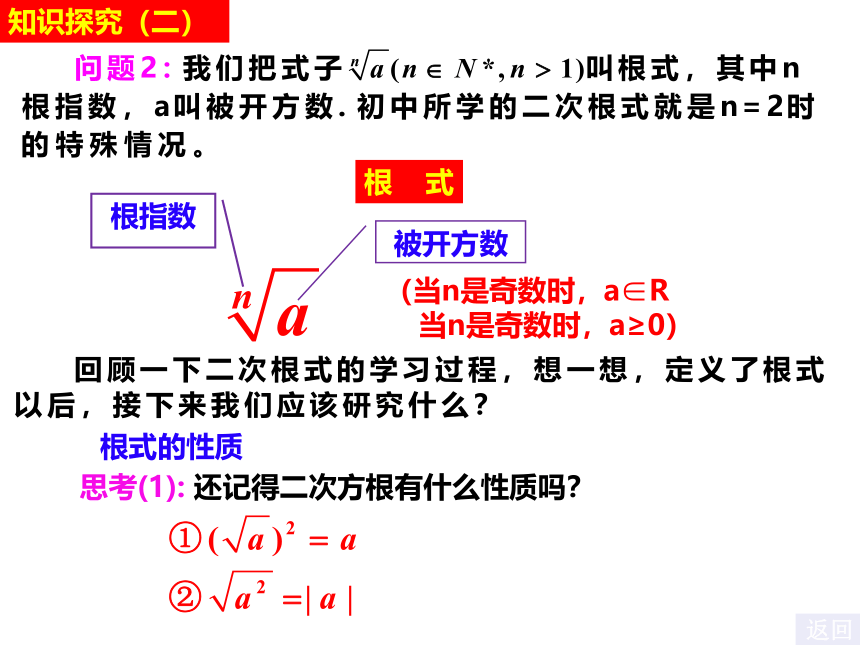
知识探究(二)
根指数
被开方数
(当n是奇数时,a∈R
当n是奇数时,a≥0)
根式
根式的性质
思考(1): 还记得二次方根有什么性质吗?
返回
根式的性质
例 析
返回
原式=(a-1)+|1-a|+(1-a)
=|1-a|
∴当a>1时, 原式=a-1
当a=1时, 原式=0
当a<1时, 原式=1-a
练习
知识探究(三)
分数指数幂
规定分数指数幂的意义的以后, 指数的概念就由整数推广到了有理数.且整数指数幂的运算性质适应于有理数指数幂。
例如
说明:
(1)分数指数幂是根式的另一种表达形式;
(2)根式与分数指数幂可以进行互化.
2. 0的正分数指数幂等于0,0的负分数指数幂没有意义.
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
同底数相乘,底数不变,指数相加
同底数相除,底数不变,指数相减
积的乘方,每个因式分别乘方
商的乘方,分子分母分别乘方
幂的乘方,底数不变,指数相乘
练习
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
例 析
练习
教材P109练习第2,3题
1.整数指数幂是按怎样的路径推广到有理数指数幂的?你能画出一个结构图来表示这个过程吗?
小 结
n次方根
根式
定义
表示
二次方程x=a2
三次方程x=a3
... ...
分数指数幂
整数指数幂
有理数指数幂
性质
作 业
1.教材P109习题4.1A组:第1,4,5题
第四章 指数函数对数函数
4.1指数
4.1.1 n次方根与分数指数幂
引入
良渚遗址位于浙江省杭州市余杭区良渚和瓶窑镇,1936年首次发现. 这里的巨型城址,面积近360万平方米,包括古城、水坝和多处高等级建筑. 考古学家利用遗址中遗存的碳14的残留量测定,古城存在的时期为公元前3300年~2500年,你知道考古学家测定遗址年代用的是什么数学知识吗?
实际上,考古学家所用的数学知识就是本章即将要学习的指数函数. 指数函数在解决实际问题中有着广泛的应用. 例如,在自然条件下,细胞的分裂、人口的增长、放射性物质的衰减等问题,都可利用指数函数构建数学模型来刻画它们的变化规律。
通过幂函数的学习,我们已经体验了研究一类函数的过程和方法. 在本章,我们将类比幂函数的研究方法,学习指数函数和对数函数的概念、图象和性质,并对这三类基本初等函数的变化规律的差异进行比较,在此基础上,通过解决简单的实际问题,体会如何根据变化差异,选择合适和函数类型构建数学模型,刻画现实问题的变化规律。
本节(4.1指数)要学习的内容和过程大致为
(1)将根式的概念推广到n次方根;
(2)利用n次方根的定义和运算,定义分数指数幂,把幂中
的指数x的范围推广到有理数;
(3)类比从有理数扩充到实数的过程,把有理数指数幂推广
到实数指数幂.
为了研究指数函数,我们需要将指数的范围拓展到全体实数.
初中已经学过整数指数幂,负指数幂、零指数幂,有学习幂
函数时,我们把正方形场地的边长 c关于面积S的函数
知识探究(一)
问题1:初中阶段我们学过平方根、立方根的概念,你能回想出这些概念吗?能举例说明吗?
思考(1): 类比平方根,立方根,你能写出4次方根,5次方根,... ...,n 次方根的规定吗?
一般地,如果xn=a(n∈N*且n>1),那么x叫a的n次方根.
n次方根
思考(2): 任何实数a都一定有n 次方根吗?如何有,有几个呢?请举例说明.
(1)当n是奇数时,
任意实数a都有n次方根,且只有一个. 记作:
(2)当n是偶数时,
①若a>0,则a有n次方根, 且有两个. 记作:
②若a=0,则a有n次方根, 且只有一个0,即
③若a<0,则a的n次方根不存在.
说明:
为什么负数没有偶次方根?
返回
知识探究(二)
根指数
被开方数
(当n是奇数时,a∈R
当n是奇数时,a≥0)
根式
根式的性质
思考(1): 还记得二次方根有什么性质吗?
返回
根式的性质
例 析
返回
原式=(a-1)+|1-a|+(1-a)
=|1-a|
∴当a>1时, 原式=a-1
当a=1时, 原式=0
当a<1时, 原式=1-a
练习
知识探究(三)
分数指数幂
规定分数指数幂的意义的以后, 指数的概念就由整数推广到了有理数.且整数指数幂的运算性质适应于有理数指数幂。
例如
说明:
(1)分数指数幂是根式的另一种表达形式;
(2)根式与分数指数幂可以进行互化.
2. 0的正分数指数幂等于0,0的负分数指数幂没有意义.
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
同底数相乘,底数不变,指数相加
同底数相除,底数不变,指数相减
积的乘方,每个因式分别乘方
商的乘方,分子分母分别乘方
幂的乘方,底数不变,指数相乘
练习
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
例 析
练习
教材P109练习第2,3题
1.整数指数幂是按怎样的路径推广到有理数指数幂的?你能画出一个结构图来表示这个过程吗?
小 结
n次方根
根式
定义
表示
二次方程x=a2
三次方程x=a3
... ...
分数指数幂
整数指数幂
有理数指数幂
性质
作 业
1.教材P109习题4.1A组:第1,4,5题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
