2021-2022学年数学人教A版(2019)必修第一册4.1.2无理数指数幂及其运算性质课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册4.1.2无理数指数幂及其运算性质课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 22:02:33 | ||
图片预览






文档简介
(共17张PPT)
4.1指 数
4.1.2 无理数指数幂及性质
复习与回顾
1. 什么是n次方根?如何表示?
(2)偶次方根: 要分情况
①正数a的有两个偶次方根:
②负数没有偶次方根;
③0的偶次方根是0.
(1)奇次方根:
任意实数a都奇次方根,且只有一个:
一般地,如果xn=a(n>1且n∈N*),那么x叫a的n次方根. n次方根一般用根式表示.
2. 什么是根式?它有何性质?
根指数
被开方数
(当n是奇数时,a∈R
当n是偶数时,a≥0)
3.我们学过哪一些指数幂?
② 0的正分数指数幂等于0,0的负分数指数幂没有意义.
4. 幂的指数由整数扩展到有理数后,其运算满足那些性质?
问题:上一节我们将中ax中指数x的范围从整数扩展到了有理数,那么当指数x是无理数时,ax的意义又是什么?它还是一个确定的数吗?如果是,其运算性质又是什么?
知识探究
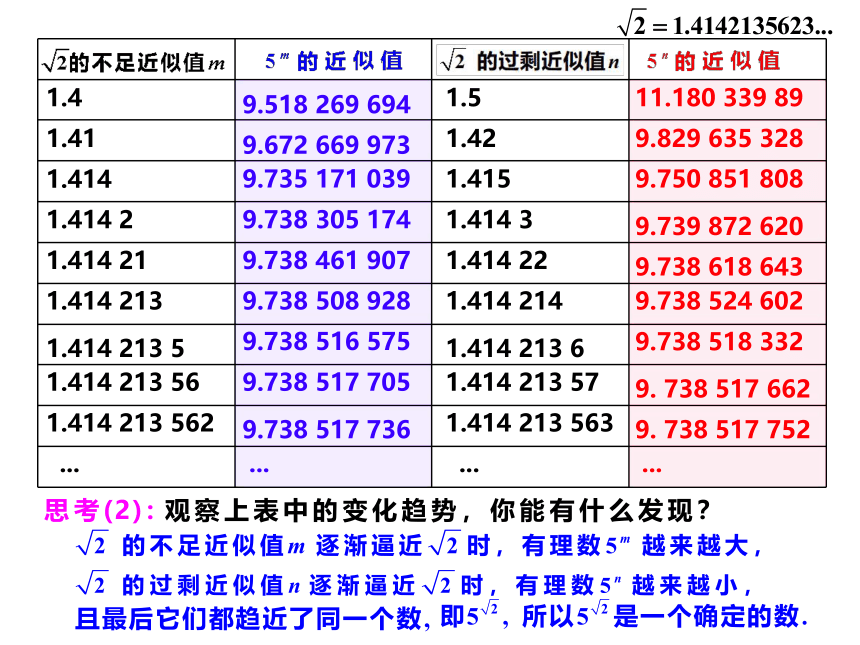
1.4
1.41
1.414
1.414 2
1.414 21
1.414 213
1.414 213 5
1.414 213 56
1.414 213 562
...
9.738 305 174
9.738 461 907
9.738 508 928
9.738 516 575
9.672 669 973
9.735 171 039
9.518 269 694
9.738 517 705
9.738 517 736
...
1.5
1.42
1.415
1.414 3
1.414 22
1.414 214
1.414 213 6
1.414 213 57
1.414 213 563
...
11.180 339 89
9.829 635 328
9.750 851 808
9.739 872 620
9.738 618 643
9.738 524 602
9.738 518 332
9. 738 517 662
9. 738 517 752
...
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
无理数指数幂的意义
返回
练习
|x| 1 2 3 4 5 6 7 8 9 10 11 ...
x
2x
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
...
例析
关于指数幂运算的几个问题:
(1)题目未作说明时,都默认其中字母的取值使式子有意义;
(2)运算时,①小数和分数一般统一化成分数,根式和分数指数幂一般统一化为分数指数幂;②注意乘法公式的应用
(3)最后结果只能保留根式或分数指数幂的一种,分式和负指数幂的一种。
一般地,原式全为根式保留根式,最后结果中的负整指数幂化为分式(数).
返回
练习
例析
思考:对于条件求值的问题你有什么认识?
(1)一般情况下,先化简,再求值;
(2)若给出的字母未知或不易求出,可构造出已知条件的结构,再整体代入;
(3)注意乘法公式的变形及应用。
返回
思考:若a∈(0,1),那么情况会怎样?
练习
课堂小结
1.整数指数幂是怎样的路扩展到实数指数幂的?
2.指数幂(含根式)的运算要注意哪一些问题?
3.条件求值要注意哪一些问题?
作业
2. 教材P110习题4.1第7,8题
4.1指 数
4.1.2 无理数指数幂及性质
复习与回顾
1. 什么是n次方根?如何表示?
(2)偶次方根: 要分情况
①正数a的有两个偶次方根:
②负数没有偶次方根;
③0的偶次方根是0.
(1)奇次方根:
任意实数a都奇次方根,且只有一个:
一般地,如果xn=a(n>1且n∈N*),那么x叫a的n次方根. n次方根一般用根式表示.
2. 什么是根式?它有何性质?
根指数
被开方数
(当n是奇数时,a∈R
当n是偶数时,a≥0)
3.我们学过哪一些指数幂?
② 0的正分数指数幂等于0,0的负分数指数幂没有意义.
4. 幂的指数由整数扩展到有理数后,其运算满足那些性质?
问题:上一节我们将中ax中指数x的范围从整数扩展到了有理数,那么当指数x是无理数时,ax的意义又是什么?它还是一个确定的数吗?如果是,其运算性质又是什么?
知识探究
1.4
1.41
1.414
1.414 2
1.414 21
1.414 213
1.414 213 5
1.414 213 56
1.414 213 562
...
9.738 305 174
9.738 461 907
9.738 508 928
9.738 516 575
9.672 669 973
9.735 171 039
9.518 269 694
9.738 517 705
9.738 517 736
...
1.5
1.42
1.415
1.414 3
1.414 22
1.414 214
1.414 213 6
1.414 213 57
1.414 213 563
...
11.180 339 89
9.829 635 328
9.750 851 808
9.739 872 620
9.738 618 643
9.738 524 602
9.738 518 332
9. 738 517 662
9. 738 517 752
...
一般地,在指数幂ax中,为了保证对x取所有情况有意义,通常规定底数a>0. 但在具体问题中,只需使指数幂ax有意义即可。
无理数指数幂的意义
返回
练习
|x| 1 2 3 4 5 6 7 8 9 10 11 ...
x
2x
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
...
例析
关于指数幂运算的几个问题:
(1)题目未作说明时,都默认其中字母的取值使式子有意义;
(2)运算时,①小数和分数一般统一化成分数,根式和分数指数幂一般统一化为分数指数幂;②注意乘法公式的应用
(3)最后结果只能保留根式或分数指数幂的一种,分式和负指数幂的一种。
一般地,原式全为根式保留根式,最后结果中的负整指数幂化为分式(数).
返回
练习
例析
思考:对于条件求值的问题你有什么认识?
(1)一般情况下,先化简,再求值;
(2)若给出的字母未知或不易求出,可构造出已知条件的结构,再整体代入;
(3)注意乘法公式的变形及应用。
返回
思考:若a∈(0,1),那么情况会怎样?
练习
课堂小结
1.整数指数幂是怎样的路扩展到实数指数幂的?
2.指数幂(含根式)的运算要注意哪一些问题?
3.条件求值要注意哪一些问题?
作业
2. 教材P110习题4.1第7,8题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
