13.4课题学习最短路径问题练习2021—2022学年人教版数学八年级上册 (word版,无答案)
文档属性
| 名称 | 13.4课题学习最短路径问题练习2021—2022学年人教版数学八年级上册 (word版,无答案) | 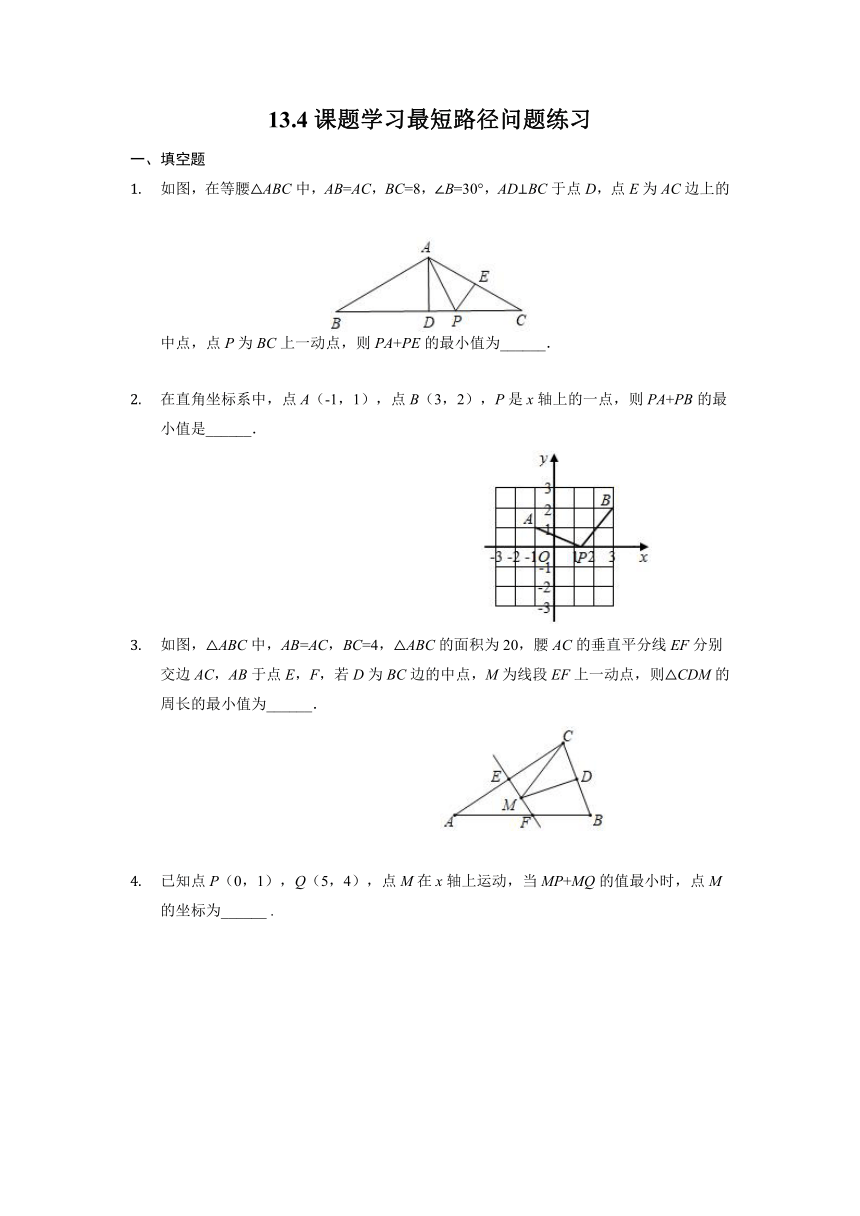 | |
| 格式 | docx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 00:52:46 | ||
图片预览


文档简介
13.4课题学习最短路径问题练习
一、填空题
如图,在等腰△ABC中,AB=AC,BC=8,∠B=30°,AD⊥BC于点D,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为______.
在直角坐标系中,点A(-1,1),点B(3,2),P是x轴上的一点,则PA+PB的最小值是______.
如图,△ABC中,AB=AC,BC=4,△ABC的面积为20,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为______.
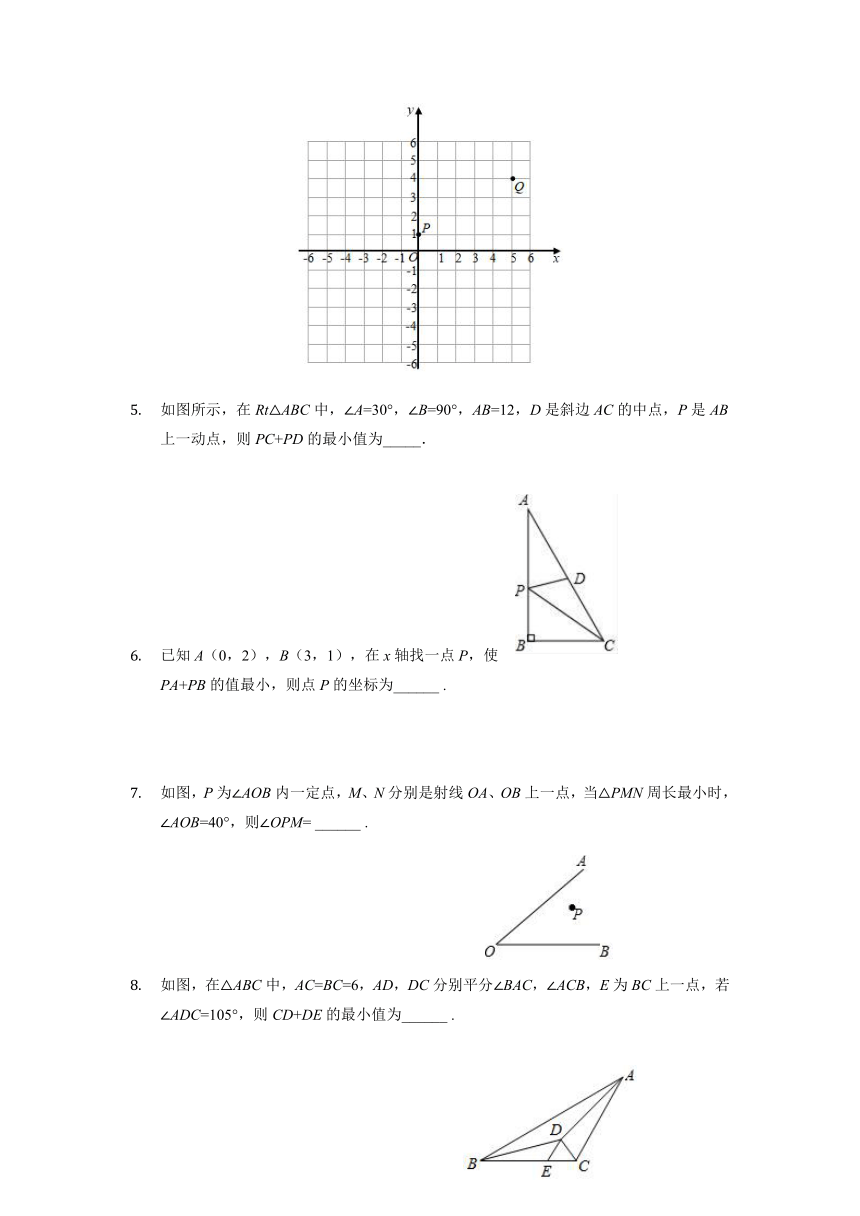
已知点P(0,1),Q(5,4),点M在x轴上运动,当MP+MQ的值最小时,点M的坐标为______ .
如图所示,在Rt△ABC中,∠A=30°,∠B=90°,AB=12,D是斜边AC的中点,P是AB上一动点,则PC+PD的最小值为_____.
已知A(0,2),B(3,1),在x轴找一点P,使PA+PB的值最小,则点P的坐标为______ .
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠AOB=40°,则∠OPM= ______ .
如图,在△ABC中,AC=BC=6,AD,DC分别平分∠BAC,∠ACB,E为BC上一点,若∠ADC=105°,则CD+DE的最小值为______ .
9.如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是 .
10.如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC= .
11.如图,在△ABC中,AB=3,AC=4,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点,
则△ABP周长的最小值是 .
12.如图,△ABC中,AB=AC,BC=5,S△ABC=15,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为__________.
13.如图,△ABC中,AB=AC=13,BC=10,AD⊥BC,BE⊥AC,P为AD上一动点,则PE+PC最小值为 .
解答题
14.如图,在大河CD的同侧有A,B两个村庄,请在大河CD的边上找到自来水厂P的位置,满足下列条件:
(1) 水厂P到A,B两个村庄的距离相等;
(2) 水厂P到A,B两个村庄的距离和最短.
15.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
16.如图,点P、Q为∠MON内两点,分别在OM与ON上找点A、B,使四边形PAQB的周长最小.
17.如图,正方形网格中每个小正方形的边长为1,网格中有一个△ABC.
(1)请直接写出△ABC的面积为______.
(2)利用方格找出点A、B、C关于直线MN的对称点D、E、F,并顺次连接D、E、F三点.
(3)若点P是直线MN上的一个动点,则PC+PA的最小值为______.
18.如图,在△ABC中,AB=AC.
(1)利用尺规作线段AB的垂直平分线DE,垂足为E,交AC于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,
①若∠A=30°,求∠DBC的度数;
②若△ABC的面积是12,BC=4,点M、N分别是BC、DE上的动点,求BN+NM的最小值.
19.如图,为了做好2013年沈阳全运会起降的交通安全工作,某交警执勤小队从A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后再到B地执行任务,他们应如何走才能使总路程最短?
21.已知:M、N分别是∠AOB的边OA、OB上的定点,
(1)如图1,若∠O=∠OMN,过M作射线MD∥OB(如图),点C是射线MD上一动点,∠MNC的平分线NE交射线OA于E点.试探究∠MEN与∠MCN的数量关系;
(2)如图2,若P是线段ON上一动点,Q是射线MA上一动点.∠AOB=20°,当MP+PQ+QN取得最小值时,求∠OPM+∠OQN的值.
22.已知点P在∠MON内.
(1)如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
①若∠MON=50°,则∠GOH= ;
②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;
(2)如图2,若∠MON=60°,A、B分别是射线OM、ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
一、填空题
如图,在等腰△ABC中,AB=AC,BC=8,∠B=30°,AD⊥BC于点D,点E为AC边上的中点,点P为BC上一动点,则PA+PE的最小值为______.
在直角坐标系中,点A(-1,1),点B(3,2),P是x轴上的一点,则PA+PB的最小值是______.
如图,△ABC中,AB=AC,BC=4,△ABC的面积为20,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为______.
已知点P(0,1),Q(5,4),点M在x轴上运动,当MP+MQ的值最小时,点M的坐标为______ .
如图所示,在Rt△ABC中,∠A=30°,∠B=90°,AB=12,D是斜边AC的中点,P是AB上一动点,则PC+PD的最小值为_____.
已知A(0,2),B(3,1),在x轴找一点P,使PA+PB的值最小,则点P的坐标为______ .
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠AOB=40°,则∠OPM= ______ .
如图,在△ABC中,AC=BC=6,AD,DC分别平分∠BAC,∠ACB,E为BC上一点,若∠ADC=105°,则CD+DE的最小值为______ .
9.如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是 .
10.如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC= .
11.如图,在△ABC中,AB=3,AC=4,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点,
则△ABP周长的最小值是 .
12.如图,△ABC中,AB=AC,BC=5,S△ABC=15,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为__________.
13.如图,△ABC中,AB=AC=13,BC=10,AD⊥BC,BE⊥AC,P为AD上一动点,则PE+PC最小值为 .
解答题
14.如图,在大河CD的同侧有A,B两个村庄,请在大河CD的边上找到自来水厂P的位置,满足下列条件:
(1) 水厂P到A,B两个村庄的距离相等;
(2) 水厂P到A,B两个村庄的距离和最短.
15.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
16.如图,点P、Q为∠MON内两点,分别在OM与ON上找点A、B,使四边形PAQB的周长最小.
17.如图,正方形网格中每个小正方形的边长为1,网格中有一个△ABC.
(1)请直接写出△ABC的面积为______.
(2)利用方格找出点A、B、C关于直线MN的对称点D、E、F,并顺次连接D、E、F三点.
(3)若点P是直线MN上的一个动点,则PC+PA的最小值为______.
18.如图,在△ABC中,AB=AC.
(1)利用尺规作线段AB的垂直平分线DE,垂足为E,交AC于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,
①若∠A=30°,求∠DBC的度数;
②若△ABC的面积是12,BC=4,点M、N分别是BC、DE上的动点,求BN+NM的最小值.
19.如图,为了做好2013年沈阳全运会起降的交通安全工作,某交警执勤小队从A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后再到B地执行任务,他们应如何走才能使总路程最短?
21.已知:M、N分别是∠AOB的边OA、OB上的定点,
(1)如图1,若∠O=∠OMN,过M作射线MD∥OB(如图),点C是射线MD上一动点,∠MNC的平分线NE交射线OA于E点.试探究∠MEN与∠MCN的数量关系;
(2)如图2,若P是线段ON上一动点,Q是射线MA上一动点.∠AOB=20°,当MP+PQ+QN取得最小值时,求∠OPM+∠OQN的值.
22.已知点P在∠MON内.
(1)如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
①若∠MON=50°,则∠GOH= ;
②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;
(2)如图2,若∠MON=60°,A、B分别是射线OM、ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
