28.1锐角三角函数(第1课时) 课件(共32张PPT)
文档属性
| 名称 | 28.1锐角三角函数(第1课时) 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 12:11:02 | ||
图片预览








文档简介
(共32张PPT)
28.1锐角三角函数
---第1课时
人教版 九年级下
教学目标
理解锐角正弦的定义,掌握当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变). (重点)
能利用正弦概念解决相关问题. (重点、难点)
A
B
C
α
情境导入
比萨斜塔位于意大利中部比萨古城内的教堂广场上,该塔于1350年成时就已倾斜,其塔顶中心点偏离垂线中心线2.1米,1972年比萨地区发生地震,这座高AB=54.5米的斜塔大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2米.仔细看下图,你能用塔身中心线与垂直中心线所成的角度来描述比萨斜塔的倾斜程度吗?
从数学角度看,上述问题就是:已知直角三角形的某些边长,求其锐角的度数。对于直角三角形,我们已经知道三边之间、两个锐角之间的关系,它的边角之间有什么关系呢?下面我们一起来探究一下!
合作探究
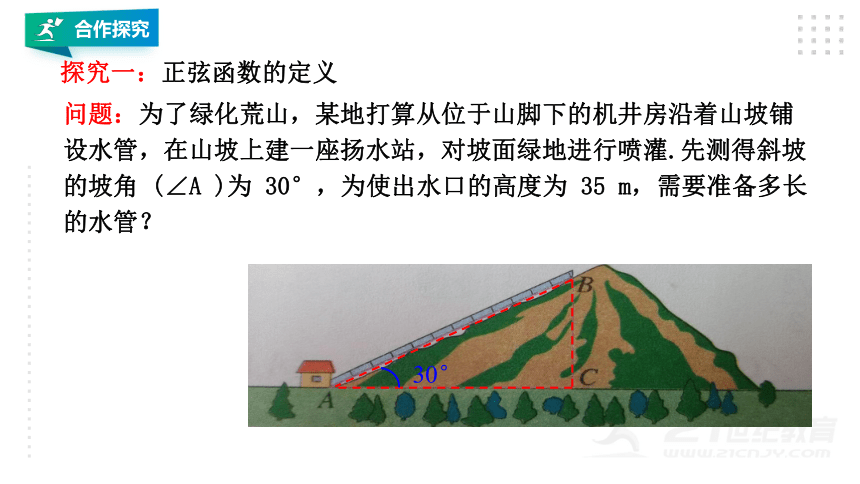
问题:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌.先测得斜坡的坡角 (∠A )为 30°,为使出水口的高度为 35 m,需要准备多长的水管?
30°
探究一:正弦函数的定义
合作探究
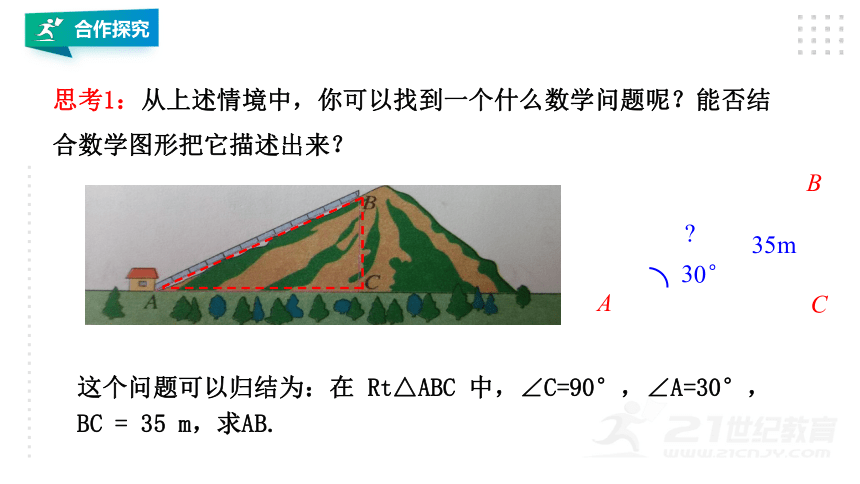
思考1:从上述情境中,你可以找到一个什么数学问题呢?能否结合数学图形把它描述出来?
A
B
C
30°
35m
这个问题可以归结为:在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
合作探究
A
B
C
30°
35m
如图,在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
根据“在直角三角形中,30°角所对的
边等于斜边的一半”, 即
可得 AB = 2BC =2×35=70 (m).
也就是说,需要准备 70 m 长的水管.
思考2:如果出水口的高度为50 m,那么需要准备多长的水管?60米呢?
100米
120米
合作探究
归纳总结:
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
合作探究
思考3:如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A的对边与斜边的比 由此你能得出什么结论?
解:因为∠A=45°,∠C=90°,
所以AC=BC,由勾股定理得:
AB2=AC2+BC2=2BC2,
所以
因此
A
B
C
合作探究
在直角三角形中,如果一个锐角等于45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
归纳总结:
合作探究
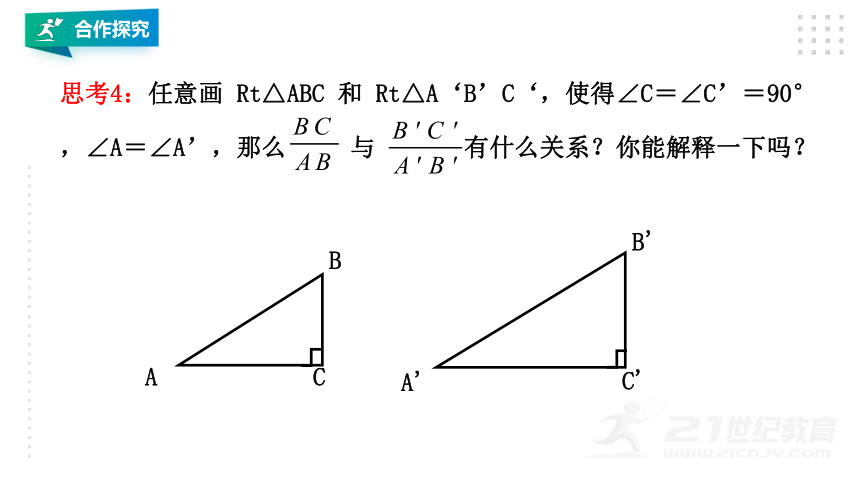
思考4:任意画 Rt△ABC 和 Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A’,那么 与 有什么关系?你能解释一下吗?
A
B
C
A'
B'
C'
合作探究
因为
所以Rt△ABC∽Rt△
因此
即
这就是说,在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个固定值.
合作探究
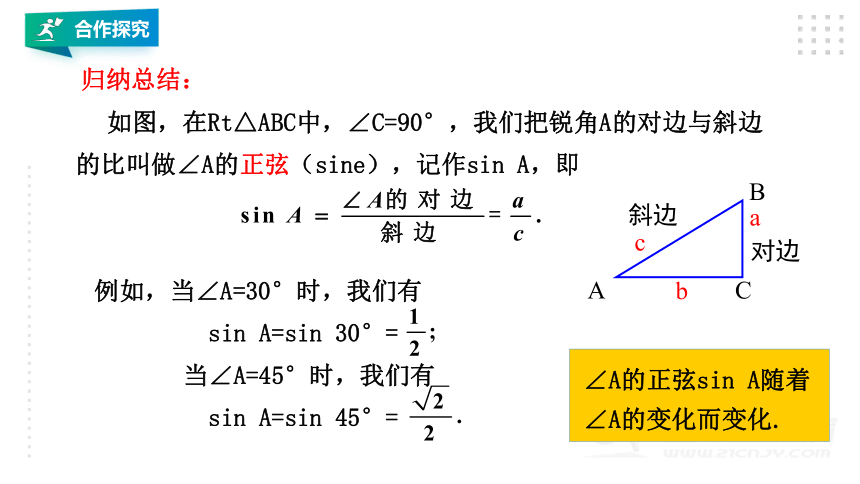
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sin A,即
例如,当∠A=30°时,我们有
sin A=sin 30°=
当∠A=45°时,我们有
sin A=sin 45°=
∠A的正弦sin A随着∠A的变化而变化.
A
B
C
c
a
b
对边
斜边
归纳总结:
典例精析
例1 如图,在 Rt△ABC 中,∠C=90°,求 sinA 和sinB 的值.
A
B
C
4
3
图①
?
A
B
C
13
5
图②
?
典例精析
解:如图①,在 Rt△ABC 中,由勾股定理得
因此
如图②,在Rt△ABC中,由勾股定理得
因此
知识点拨:求sin A就是要确定∠A的对边与斜边的比;求sin B就是要确定∠B的对边与斜边的比.
趁热打铁
sinA = ( )
sinA = ( )
1. 如图,判断对错:
A
6m
8m
B
C
√
×
sinB = ( )
×
sinA =0.6 ( )
sinB =0.8 ( )
√
√
趁热打铁
3、把Rt △ABC三边的长度都扩大为原来的5倍,则锐角∠A的正弦值
( )
A.不变 B.缩小为原来的 C.扩大为原来5倍 D.不能确定
A
2、如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
知识点拨:结合平面直角坐标系求某角的正弦函数值,一般过已知点向x轴或y轴作垂线,构造直角三角形,再结合勾股定理求解.
趁热打铁
4、如图,在Rt△ABC中,∠C=90°, 求sin A和sin B的值.
(1)解:由勾股定理得
所以
趁热打铁
(2)解:由勾股定理得
∴
合作探究
探究二:利用正弦函数求边长
例2、 如图,在 Rt△ABC 中,∠C=90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
A
B
C
知识点拨:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长,然后再利用勾股定理,求出 AC 的长度,进而求出 sinB 及 Rt△ABC 的面积.
合作探究
解:∵∠C=90°, ∴
∴ AB = 3BC =3×3=9.
∴
∴
∴
A
B
C
趁热打铁
1、在Rt △ABC中,∠C=90°,BC=2,sin A= 则边AC的长是
( )
A. B.3
C. D.
A
2、在Rt△ABC中,∠C=90°,AC=9,sin B= ,则AB的长等于
( )
A.15 B.12 C.9 D.6
A
趁热打铁
3、在 △ABC 中,∠C=90°,AC=24cm,sinA= ,求这个三角形的周长.
解:由sinA= ,设BC=7x,则AB=25x.
在 Rt△ABC中,由勾股定理得
即 24x = 24cm,解得 x = 1 cm.
故 BC = 7x = 7 cm,AB = 25x = 25 cm.
所以 △ABC 的周长为: BC+AC+AB = 7+24+25 = 56 (cm).
知识点拨:由正弦值求边长,当已知角的对边或斜边长时通常先根据某个锐角的正弦的定义确定斜边或对边,根据勾股定理求另一边;当已知角的邻边时,根据正弦函数的定义确定另外两边的比值,根据勾股定理列方程求解即可.
综合演练
2、在Rt △ABC中,∠C=90°,AB=13,AC=5,则sin A的值为( )
B. C. D.
B
1、 如图, 在△ABC中,∠B=90°,sinA的值为 ( )
7
A
C
B
3
A. B.
C. D.
A
综合演练
3、如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α的值是( )
A. B. C. D.
D
4、在Rt△ABC中,∠C=90°,若AB=4,sin A= ,则斜边上的高等于 。
综合演练
5、 如图,在正方形网格中有 △ABC,
则 sin∠ABC的值为 .
6、如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF= 。
综合演练
7. 如图,点 D (0,3),O (0,0),C (4,0)在 ⊙A 上,BD是 ⊙A 的一条弦,则 sin∠OBD =______.
知识点拨:连接 CD,可得出 ∠OBD = ∠OCD,根据点 D (0,3),C(4,0),得 OD = 3,OC = 4,由勾股定理得出 CD = 5,再在直角三角形中得出利用三角函数求出sin∠OCD 即可.
O
x
y
A
C
B
D
综合演练
8. 如图,在 △ABC 中, AB = BC = 5,sinA = ,求△ABC 的面积.
D
5
5
C
B
A
解:作BD⊥AC于点D,
∵ sinA = ,
∴
又∵ AB=AC ,BD⊥AC,∴ AC=2AD=6,
∴S△ABC=AC×BD÷2=12.
提能训练
9. 如图,在 △ABC 中,∠ACB=90°,CD⊥AB.
(1) sinB 可以由哪两条线段之比表示
A
C
B
D
解:∵ CD⊥AB,∴∠ADC =∠ACB = 90°,
∴∠ACD = ∠B=90°-∠A,
∴
(2) 若 AC = 5,CD = 3,求 sinB 的值.
解:
由 (1)知,
课堂总结
说一说:
1、什么是正弦函数?
2、如何利用正弦函数
本节课你有哪些收获?
作业布置
P64练习:2
习题28.1 P68页:6
https://www.21cnjy.com/help/help_extract.php
28.1锐角三角函数
---第1课时
人教版 九年级下
教学目标
理解锐角正弦的定义,掌握当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变). (重点)
能利用正弦概念解决相关问题. (重点、难点)
A
B
C
α
情境导入
比萨斜塔位于意大利中部比萨古城内的教堂广场上,该塔于1350年成时就已倾斜,其塔顶中心点偏离垂线中心线2.1米,1972年比萨地区发生地震,这座高AB=54.5米的斜塔大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2米.仔细看下图,你能用塔身中心线与垂直中心线所成的角度来描述比萨斜塔的倾斜程度吗?
从数学角度看,上述问题就是:已知直角三角形的某些边长,求其锐角的度数。对于直角三角形,我们已经知道三边之间、两个锐角之间的关系,它的边角之间有什么关系呢?下面我们一起来探究一下!
合作探究
问题:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌.先测得斜坡的坡角 (∠A )为 30°,为使出水口的高度为 35 m,需要准备多长的水管?
30°
探究一:正弦函数的定义
合作探究
思考1:从上述情境中,你可以找到一个什么数学问题呢?能否结合数学图形把它描述出来?
A
B
C
30°
35m
这个问题可以归结为:在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
合作探究
A
B
C
30°
35m
如图,在 Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m,求AB.
根据“在直角三角形中,30°角所对的
边等于斜边的一半”, 即
可得 AB = 2BC =2×35=70 (m).
也就是说,需要准备 70 m 长的水管.
思考2:如果出水口的高度为50 m,那么需要准备多长的水管?60米呢?
100米
120米
合作探究
归纳总结:
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
合作探究
思考3:如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A的对边与斜边的比 由此你能得出什么结论?
解:因为∠A=45°,∠C=90°,
所以AC=BC,由勾股定理得:
AB2=AC2+BC2=2BC2,
所以
因此
A
B
C
合作探究
在直角三角形中,如果一个锐角等于45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
归纳总结:
合作探究
思考4:任意画 Rt△ABC 和 Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A’,那么 与 有什么关系?你能解释一下吗?
A
B
C
A'
B'
C'
合作探究
因为
所以Rt△ABC∽Rt△
因此
即
这就是说,在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个固定值.
合作探究
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sin A,即
例如,当∠A=30°时,我们有
sin A=sin 30°=
当∠A=45°时,我们有
sin A=sin 45°=
∠A的正弦sin A随着∠A的变化而变化.
A
B
C
c
a
b
对边
斜边
归纳总结:
典例精析
例1 如图,在 Rt△ABC 中,∠C=90°,求 sinA 和sinB 的值.
A
B
C
4
3
图①
?
A
B
C
13
5
图②
?
典例精析
解:如图①,在 Rt△ABC 中,由勾股定理得
因此
如图②,在Rt△ABC中,由勾股定理得
因此
知识点拨:求sin A就是要确定∠A的对边与斜边的比;求sin B就是要确定∠B的对边与斜边的比.
趁热打铁
sinA = ( )
sinA = ( )
1. 如图,判断对错:
A
6m
8m
B
C
√
×
sinB = ( )
×
sinA =0.6 ( )
sinB =0.8 ( )
√
√
趁热打铁
3、把Rt △ABC三边的长度都扩大为原来的5倍,则锐角∠A的正弦值
( )
A.不变 B.缩小为原来的 C.扩大为原来5倍 D.不能确定
A
2、如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
知识点拨:结合平面直角坐标系求某角的正弦函数值,一般过已知点向x轴或y轴作垂线,构造直角三角形,再结合勾股定理求解.
趁热打铁
4、如图,在Rt△ABC中,∠C=90°, 求sin A和sin B的值.
(1)解:由勾股定理得
所以
趁热打铁
(2)解:由勾股定理得
∴
合作探究
探究二:利用正弦函数求边长
例2、 如图,在 Rt△ABC 中,∠C=90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
A
B
C
知识点拨:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长,然后再利用勾股定理,求出 AC 的长度,进而求出 sinB 及 Rt△ABC 的面积.
合作探究
解:∵∠C=90°, ∴
∴ AB = 3BC =3×3=9.
∴
∴
∴
A
B
C
趁热打铁
1、在Rt △ABC中,∠C=90°,BC=2,sin A= 则边AC的长是
( )
A. B.3
C. D.
A
2、在Rt△ABC中,∠C=90°,AC=9,sin B= ,则AB的长等于
( )
A.15 B.12 C.9 D.6
A
趁热打铁
3、在 △ABC 中,∠C=90°,AC=24cm,sinA= ,求这个三角形的周长.
解:由sinA= ,设BC=7x,则AB=25x.
在 Rt△ABC中,由勾股定理得
即 24x = 24cm,解得 x = 1 cm.
故 BC = 7x = 7 cm,AB = 25x = 25 cm.
所以 △ABC 的周长为: BC+AC+AB = 7+24+25 = 56 (cm).
知识点拨:由正弦值求边长,当已知角的对边或斜边长时通常先根据某个锐角的正弦的定义确定斜边或对边,根据勾股定理求另一边;当已知角的邻边时,根据正弦函数的定义确定另外两边的比值,根据勾股定理列方程求解即可.
综合演练
2、在Rt △ABC中,∠C=90°,AB=13,AC=5,则sin A的值为( )
B. C. D.
B
1、 如图, 在△ABC中,∠B=90°,sinA的值为 ( )
7
A
C
B
3
A. B.
C. D.
A
综合演练
3、如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α的值是( )
A. B. C. D.
D
4、在Rt△ABC中,∠C=90°,若AB=4,sin A= ,则斜边上的高等于 。
综合演练
5、 如图,在正方形网格中有 △ABC,
则 sin∠ABC的值为 .
6、如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF= 。
综合演练
7. 如图,点 D (0,3),O (0,0),C (4,0)在 ⊙A 上,BD是 ⊙A 的一条弦,则 sin∠OBD =______.
知识点拨:连接 CD,可得出 ∠OBD = ∠OCD,根据点 D (0,3),C(4,0),得 OD = 3,OC = 4,由勾股定理得出 CD = 5,再在直角三角形中得出利用三角函数求出sin∠OCD 即可.
O
x
y
A
C
B
D
综合演练
8. 如图,在 △ABC 中, AB = BC = 5,sinA = ,求△ABC 的面积.
D
5
5
C
B
A
解:作BD⊥AC于点D,
∵ sinA = ,
∴
又∵ AB=AC ,BD⊥AC,∴ AC=2AD=6,
∴S△ABC=AC×BD÷2=12.
提能训练
9. 如图,在 △ABC 中,∠ACB=90°,CD⊥AB.
(1) sinB 可以由哪两条线段之比表示
A
C
B
D
解:∵ CD⊥AB,∴∠ADC =∠ACB = 90°,
∴∠ACD = ∠B=90°-∠A,
∴
(2) 若 AC = 5,CD = 3,求 sinB 的值.
解:
由 (1)知,
课堂总结
说一说:
1、什么是正弦函数?
2、如何利用正弦函数
本节课你有哪些收获?
作业布置
P64练习:2
习题28.1 P68页:6
https://www.21cnjy.com/help/help_extract.php
