28.1锐角三角函数(第2课时) 课件(共27张PPT)
文档属性
| 名称 | 28.1锐角三角函数(第2课时) 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 12:15:35 | ||
图片预览




文档简介
(共27张PPT)
28.1锐角三角函数
---第2课时
人教版 九年级下
教学目标
理解余弦、正切的概念进而得到锐角三角函数的概念.
(重点)
2. 能灵活运用锐角三角函数进行相关运算. (重点、难点)
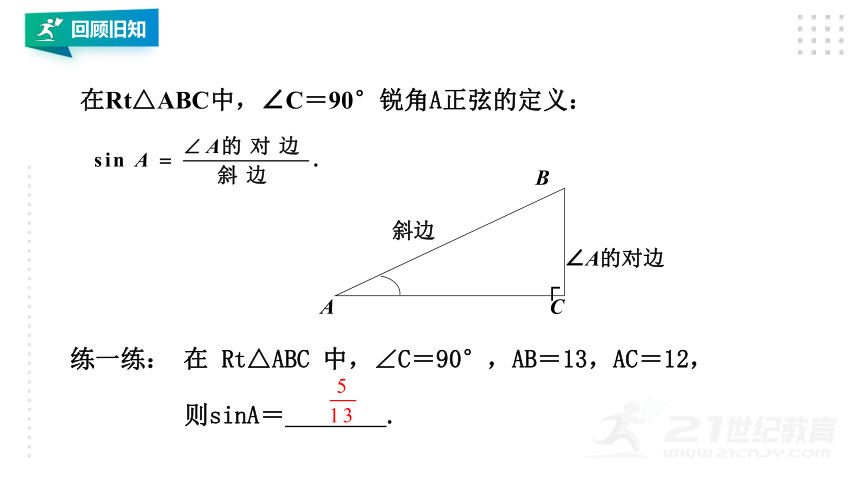
回顾旧知
在Rt△ABC中,∠C=90°锐角A正弦的定义:
A
B
C
∠A的对边
┌
斜边
练一练: 在 Rt△ABC 中,∠C=90°,AB=13,AC=12,
则sinA= .
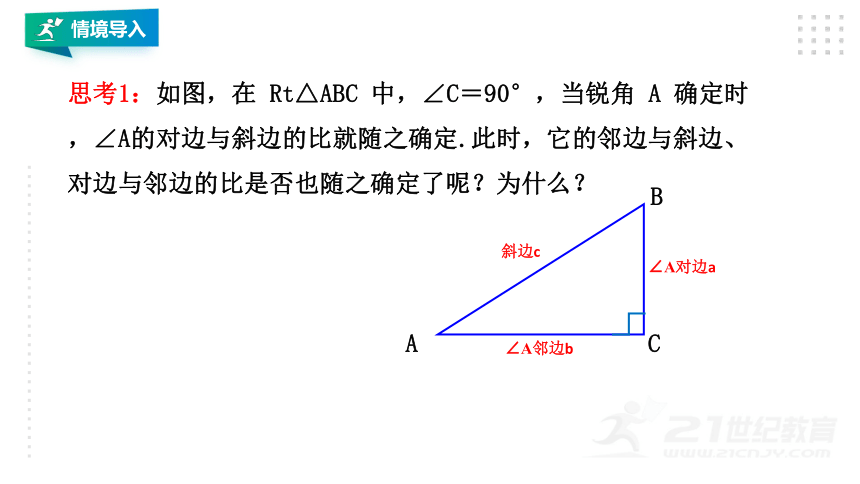
情境导入
A
B
C
思考1:如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定.此时,它的邻边与斜边、对边与邻边的比是否也随之确定了呢?为什么?
∠A邻边b
∠A对边a
斜边c
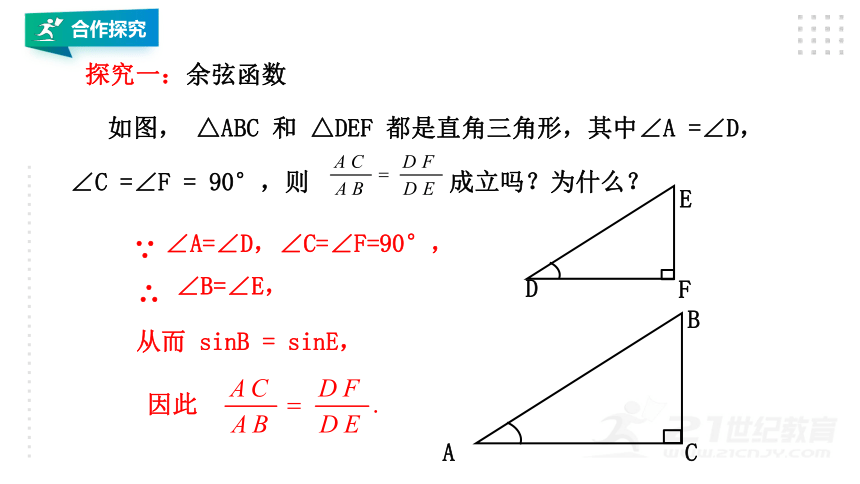
合作探究
如图, △ABC 和 △DEF 都是直角三角形,其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
探究一:余弦函数
∵
∠A=∠D,∠C=∠F=90°,
∴
∠B=∠E,
从而 sinB = sinE,
因此
合作探究
在Rt△ABC 中,当锐角A的度数一定时,无论这个直角三角形的大小如何, ∠A的邻边与斜边的比都是一个固定值。
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
归纳总结:
∠A的邻边
斜边
cos A =
A
B
C
∠A邻边b
斜边c
合作探究
思考2:如果两个角互余,那么这两个角的正弦、余弦值有什么关系?
如果两个角互余,那么其中一个角的正弦值等于另一个角的余弦值;
即:若α与β互余,则sinα= cosβ, sinβ=cosα。
例1、在 Rt△ABC 中,∠C = 90°,AB=5,BC=3, 则∠A的余弦值是( )
A. B. C. D.
C
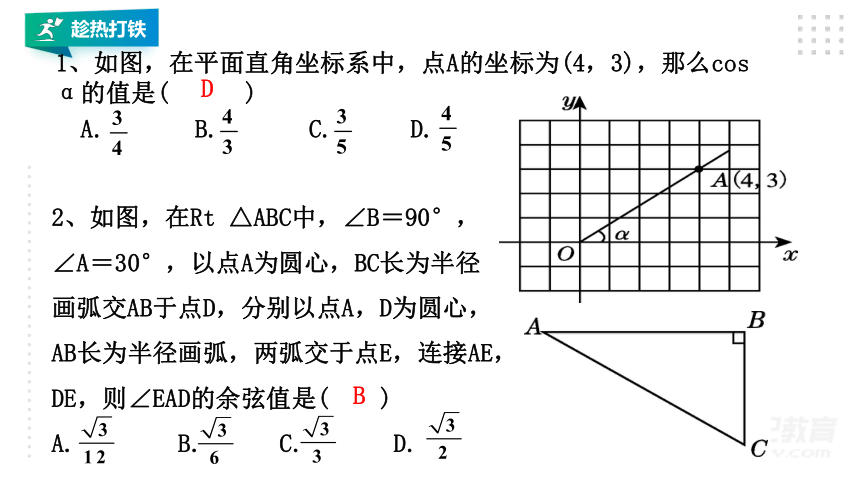
趁热打铁
1、如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( )
A. B. C. D.
D
2、如图,在Rt △ABC中,∠B=90°,
∠A=30°,以点A为圆心,BC长为半径
画弧交AB于点D,分别以点A,D为圆心,
AB长为半径画弧,两弧交于点E,连接AE,
DE,则∠EAD的余弦值是( )
A. B. C. D.
B
趁热打铁
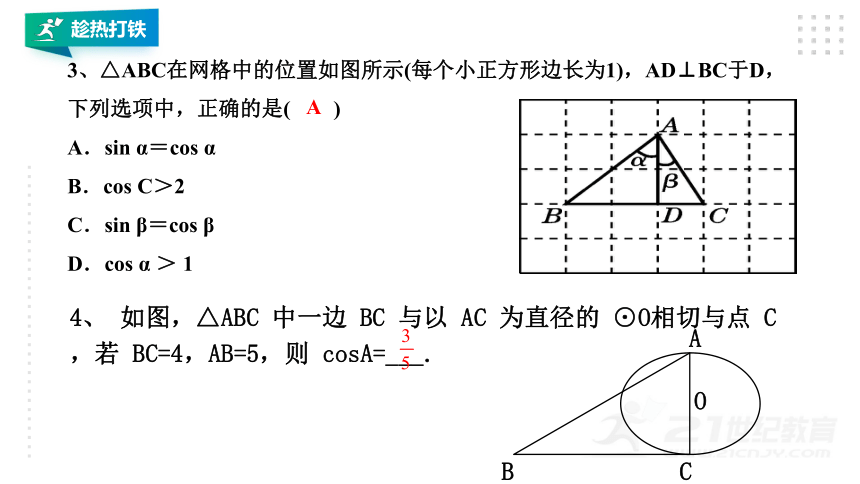
4、 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC=4,AB=5,则 cosA=___.
A
O
B
C
3、△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,正确的是( )
A.sin α=cos α
B.cos C>2
C.sin β=cos β
D.cos α > 1
A
合作探究
如图, △ABC 和 △DEF 都是直角三角形,其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
探究二:正切函数
∴ Rt△ABC ∽ Rt△DEF.
∠A=∠D ,∠C =∠F = 90°,
∵
∴
∴
合作探究
在Rt△ABC 中,当锐角A的度数一定时,无论这个直角三角形的大小如何, ∠A的对边与邻边的比都是一个固定值。
如下图所示,在直角三角形中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA ,即
归纳总结:
∠A的对边
tanA =
A
B
C
∠A邻边b
∠A的邻边
∠A对边a
锐角A的正弦、余弦、正切都是∠A 的三角函数.
合作探究
思考3:如果两个角互余,那么这两个角的正切值有什么关系?
如果两个角互余,那么这两个角的正切值互为倒数;
即:若α与β互余,则tanα. Tanβ=1。
例2、在Rt △ABC中,∠C=90°,AB=5,BC=3,则tan A的值是( )
A. B. C. D.
A
趁热打铁
1、在Rt △ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
C
2、如图,在△ABC中,∠BAC=90°,AB=AC,点D 为边AC的中点,DE⊥BC于点E,连接BD,则tan ∠DBC的值为( )
A. B.
C. D.
A
典例精析
例3: 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
趁热打铁
1、分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解: 由勾股定理得
因此:
趁热打铁
解:
所以:
综合演练
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A=26°,则直角边 BC 的长是( )
A.
B.
C.
D.
A
A
B
C
2.在Rt△ABC中,∠C=90°,且sinA= ,则下列结论正确的是( )
A.cosA= B.tanA=
C.cosA= D.tanA=
D
综合演练
4. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
A
B
C
12
13
3. sin65°,cos65°,tan65°的大小关系是( )
A. tan65°<cos65°<sin65°
B. cos65°<tan65°<sin65°
C. sin65°<cos65°<tan65°
D. cos65°<sin65°<tan65°
D
综合演练
5.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC最小的角为∠A,那么tan A的值为___________.
6.如图,点A,B,O是正方形网格上的三个格点,⊙O的半径为OA,点P是AMB上的一点,则tan ∠APB的值是 。
︵
1
M
综合演练
A
B
C
8
解:∵
7.如图,在 Rt△ABC 中,∠C = 90°,AC = 8,tanA= , 求sinA,cosA 的值.
∴
∴
∴
综合演练
8. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,求 sinA、tanA 的值.
解:在 Rt△ABC 中,由
A
B
C
设 AC = 15k,则 AB = 17k.
∴
∴
综合演练
8. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若AD = 9,CD =12. 求 tanB 的值.
解: ∵ CD⊥AB,
∠ACB= ∠ADC =90°,
∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,
∴∠B = ∠ACD,
∴ tan∠B = tan∠ACD =
提能训练
9. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB 及tanB 的值。
解:过点 A 作 AD⊥BC 于点 D.
∵ AB = AC,BC=6,
∴ BD = CD = 3,
在 Rt△ABD 中,
∴ tanB =
A
B
C
∴
D
知识点拨:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
课堂总结
本节课你有哪些收获?
(1)∠A的邻边与斜边的比叫做∠A的余弦,记作cos A,
即cos A=
(2)∠A的对边与邻边的比叫做∠A的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
作业布置
习题28.1 P68页:1、4
https://www.21cnjy.com/help/help_extract.php
28.1锐角三角函数
---第2课时
人教版 九年级下
教学目标
理解余弦、正切的概念进而得到锐角三角函数的概念.
(重点)
2. 能灵活运用锐角三角函数进行相关运算. (重点、难点)
回顾旧知
在Rt△ABC中,∠C=90°锐角A正弦的定义:
A
B
C
∠A的对边
┌
斜边
练一练: 在 Rt△ABC 中,∠C=90°,AB=13,AC=12,
则sinA= .
情境导入
A
B
C
思考1:如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定.此时,它的邻边与斜边、对边与邻边的比是否也随之确定了呢?为什么?
∠A邻边b
∠A对边a
斜边c
合作探究
如图, △ABC 和 △DEF 都是直角三角形,其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
探究一:余弦函数
∵
∠A=∠D,∠C=∠F=90°,
∴
∠B=∠E,
从而 sinB = sinE,
因此
合作探究
在Rt△ABC 中,当锐角A的度数一定时,无论这个直角三角形的大小如何, ∠A的邻边与斜边的比都是一个固定值。
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
归纳总结:
∠A的邻边
斜边
cos A =
A
B
C
∠A邻边b
斜边c
合作探究
思考2:如果两个角互余,那么这两个角的正弦、余弦值有什么关系?
如果两个角互余,那么其中一个角的正弦值等于另一个角的余弦值;
即:若α与β互余,则sinα= cosβ, sinβ=cosα。
例1、在 Rt△ABC 中,∠C = 90°,AB=5,BC=3, 则∠A的余弦值是( )
A. B. C. D.
C
趁热打铁
1、如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( )
A. B. C. D.
D
2、如图,在Rt △ABC中,∠B=90°,
∠A=30°,以点A为圆心,BC长为半径
画弧交AB于点D,分别以点A,D为圆心,
AB长为半径画弧,两弧交于点E,连接AE,
DE,则∠EAD的余弦值是( )
A. B. C. D.
B
趁热打铁
4、 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC=4,AB=5,则 cosA=___.
A
O
B
C
3、△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,正确的是( )
A.sin α=cos α
B.cos C>2
C.sin β=cos β
D.cos α > 1
A
合作探究
如图, △ABC 和 △DEF 都是直角三角形,其中∠A =∠D,∠C =∠F = 90°,则 成立吗?为什么?
A
B
C
D
E
F
探究二:正切函数
∴ Rt△ABC ∽ Rt△DEF.
∠A=∠D ,∠C =∠F = 90°,
∵
∴
∴
合作探究
在Rt△ABC 中,当锐角A的度数一定时,无论这个直角三角形的大小如何, ∠A的对边与邻边的比都是一个固定值。
如下图所示,在直角三角形中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA ,即
归纳总结:
∠A的对边
tanA =
A
B
C
∠A邻边b
∠A的邻边
∠A对边a
锐角A的正弦、余弦、正切都是∠A 的三角函数.
合作探究
思考3:如果两个角互余,那么这两个角的正切值有什么关系?
如果两个角互余,那么这两个角的正切值互为倒数;
即:若α与β互余,则tanα. Tanβ=1。
例2、在Rt △ABC中,∠C=90°,AB=5,BC=3,则tan A的值是( )
A. B. C. D.
A
趁热打铁
1、在Rt △ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
C
2、如图,在△ABC中,∠BAC=90°,AB=AC,点D 为边AC的中点,DE⊥BC于点E,连接BD,则tan ∠DBC的值为( )
A. B.
C. D.
A
典例精析
例3: 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
趁热打铁
1、分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解: 由勾股定理得
因此:
趁热打铁
解:
所以:
综合演练
1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A=26°,则直角边 BC 的长是( )
A.
B.
C.
D.
A
A
B
C
2.在Rt△ABC中,∠C=90°,且sinA= ,则下列结论正确的是( )
A.cosA= B.tanA=
C.cosA= D.tanA=
D
综合演练
4. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.
A
B
C
12
13
3. sin65°,cos65°,tan65°的大小关系是( )
A. tan65°<cos65°<sin65°
B. cos65°<tan65°<sin65°
C. sin65°<cos65°<tan65°
D. cos65°<sin65°<tan65°
D
综合演练
5.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC最小的角为∠A,那么tan A的值为___________.
6.如图,点A,B,O是正方形网格上的三个格点,⊙O的半径为OA,点P是AMB上的一点,则tan ∠APB的值是 。
︵
1
M
综合演练
A
B
C
8
解:∵
7.如图,在 Rt△ABC 中,∠C = 90°,AC = 8,tanA= , 求sinA,cosA 的值.
∴
∴
∴
综合演练
8. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,求 sinA、tanA 的值.
解:在 Rt△ABC 中,由
A
B
C
设 AC = 15k,则 AB = 17k.
∴
∴
综合演练
8. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,垂足为 D. 若AD = 9,CD =12. 求 tanB 的值.
解: ∵ CD⊥AB,
∠ACB= ∠ADC =90°,
∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,
∴∠B = ∠ACD,
∴ tan∠B = tan∠ACD =
提能训练
9. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB 及tanB 的值。
解:过点 A 作 AD⊥BC 于点 D.
∵ AB = AC,BC=6,
∴ BD = CD = 3,
在 Rt△ABD 中,
∴ tanB =
A
B
C
∴
D
知识点拨:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
课堂总结
本节课你有哪些收获?
(1)∠A的邻边与斜边的比叫做∠A的余弦,记作cos A,
即cos A=
(2)∠A的对边与邻边的比叫做∠A的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
作业布置
习题28.1 P68页:1、4
https://www.21cnjy.com/help/help_extract.php
