数据的离散程度

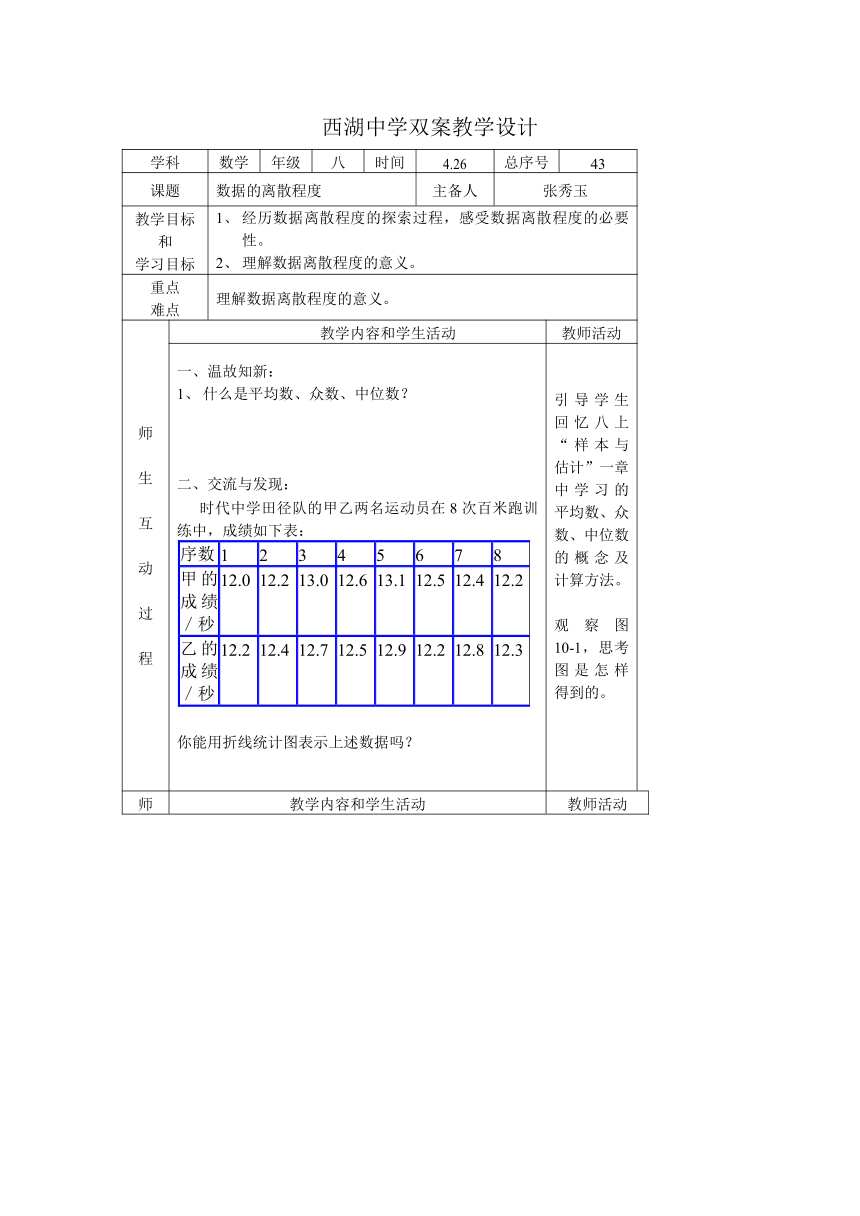
西湖中学双案教学设计
学科 数学 年级 八 时间 4.26 总序号 43
课题 数据的离散程度 主备人 张秀玉
教学目标和学习目标 经历数据离散程度的探索过程，感受数据离散程度的必要性。理解数据离散程度的意义。
重点难点 理解数据离散程度的意义。
师生互动过程 教学内容和学生活动 教师活动
温故知新：什么是平均数、众数、中位数？交流与发现：时代中学田径队的甲乙两名运动员在8次百米跑训练中，成绩如下表：序数12345678甲的成绩／秒12.012.213.012.613.112.512.412.2乙的成绩／秒12.212.412.712.512.912.212.812.3你能用折线统计图表示上述数据吗？ 引导学生回忆八上“样本与估计”一章中学均数、众数、中位数的概念及计算方法。观察图10-1，思考图是怎样得到的。
师生互动过程 教学内容和学生活动 教师活动
（1）在这8次训练中，甲、乙两名运动员的百米跑成绩的平均数、众数、中位数分别是多少？（2）小亮说:“甲、乙两名运动员的百米跑成绩的平均数、众数中位数对应相同，因此他们的成绩一样”，你认为这种说法合适吗？ （3）观察图象，你发现哪名运动员的成绩波动较大？谁的成绩比较稳定？由此你认为分析一组数据，仅关心这组数据的平均数、众数、中位数，就能得到前面的结论吗？　我们通常用数据的离散程度来描述一组数据的波动范围和偏离平均数的差异程度．数据的离散程度越大，表示数据分布的范围越广，越不稳定，平均数的代表性也就越小；数据的离散程度越小，表示数据分布的越集中，变动范围越小，平均数的代表性就越大．在实际生活和生产中，我们除了关心数据的集中趋势（平均数、中位数、众数）外，还要关注数据的离散程度，即一组数据的波动范围． 要求同学认真计算甲乙两名运动员训练成绩的平均数、众数和中位数，并进行比较。引导同学们讨论交流，说明自己意见。（3）在学生讨论的基础上引导学生说出甲、乙训练成绩的波动范围。以及比较两组数据偏离平均数的差异程度。说出相应的结论。师概括。
师生互动过程 教学内容和学生活动 教师活动
你能举出类似的例子吗？达标测试：某砖厂从生产的甲、乙两种水泥砖中，各随机抽取了10 块，分别测出了它们的抗断强度．数据如下（单位：千克／平方厘米）:甲种砖：32.50 29.66 31.64 30.00 31.77 31.01 30.76 31.24 31.87 31.05乙种砖：31.00 29.56 32.02 33.00 29.32 30.37 29.98 31.35 32.86 32.04 (1）甲种砖的平均抗断强度是多少？
(2）乙种砖的平均抗断强度是多少？
(3）作出统计图，你发现哪种砖的抗断强度波动较大？四、自我小结3、甲、乙两支仪仗队队员的身高（单位：厘米）如下：甲队：178 177 179 178 177 178 177 179 178 179 乙队： 178 179 176 178 180 178 176 178 177 180 生板演师巡回对学困生进行指导
师生互动过程 教学内容和学生活动 教师活动
（1）甲、乙两队队员的平均身高分别是多少？（2）作处折线统计图，你发现哪个对的身高比较整齐？ 限时作业
师 生 收 获 及 反 思
本节教学内容，应提供大量关于数据波动的实例，并开展充分的交流，要求学生能了解离散程度的意义，会绘制和观察折线图，能对简单问题作出判断。 学生在绘制方面耽误了不少时间。