25.2平行线分线段成比例 同步能力达标测评 2021-2022学年冀教版九年级数学上册 (Word版 含答案)
文档属性
| 名称 | 25.2平行线分线段成比例 同步能力达标测评 2021-2022学年冀教版九年级数学上册 (Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 295.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-17 19:52:19 | ||
图片预览

文档简介
2021-2022学年冀教版九年级数学上册《25.2平行线分线段成比例》
同步能力达标测评(附答案)
一.选择题(共17小题,满分85分)
1.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=4,BC=5,EF=4,那么DE的长是( )
A. B. C.3 D.
2.如图,在△ABC中,点D,E、F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列式于一定正确的是( )
A. B. C. D.
3.在△ABC中,点D、E分别在边AB、AC上,AD=2,AB=6,那么下列各条件中,不—定能判定DE∥BC的是( )
A. B. C. D.
4.如图,已知点D为△ABC边AB上一点,AD:AB=2:3,过点D作BC的平行线交AC于点E,若AE=6,则EC的长度是( )
A.1 B.2 C.3 D.4
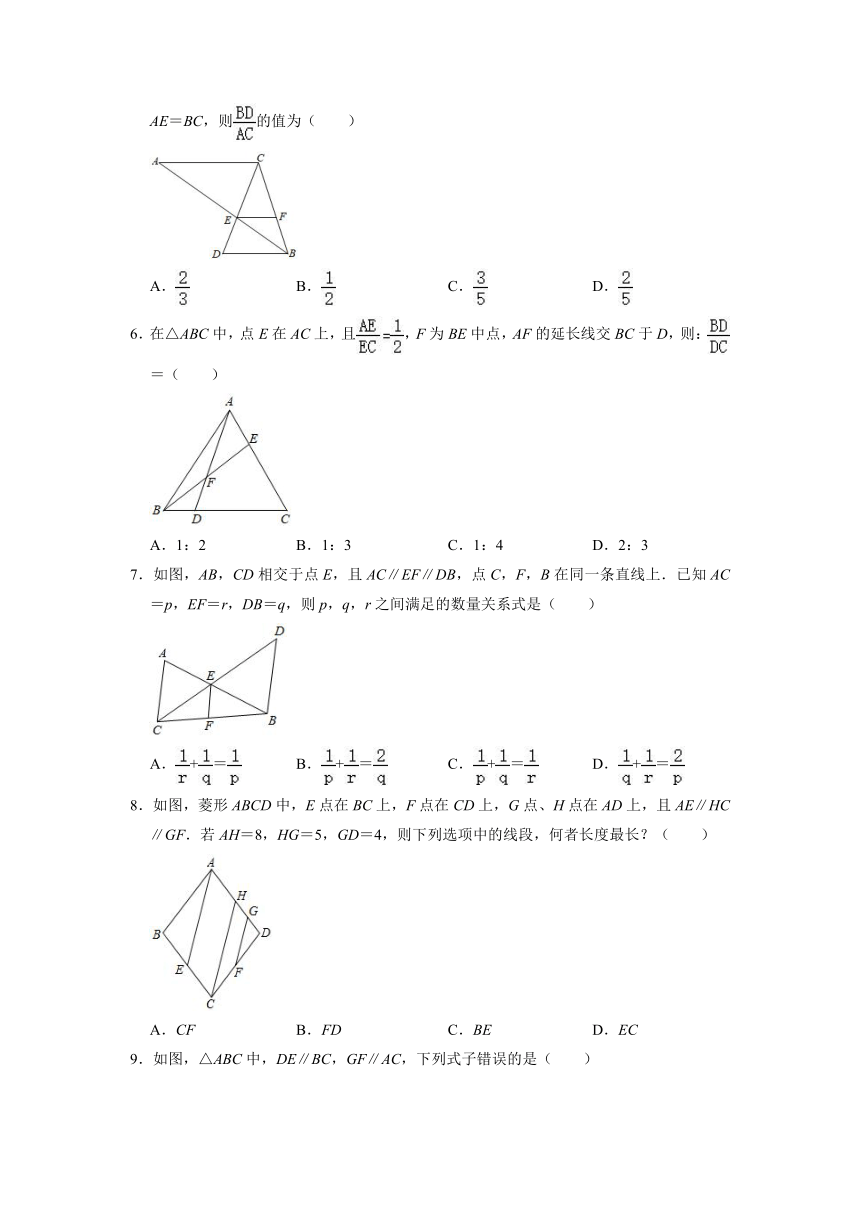
5.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
6.在△ABC中,点E在AC上,且,F为BE中点,AF的延长线交BC于D,则:=( )
A.1:2 B.1:3 C.1:4 D.2:3
7.如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
8.如图,菱形ABCD中,E点在BC上,F点在CD上,G点、H点在AD上,且AE∥HC∥GF.若AH=8,HG=5,GD=4,则下列选项中的线段,何者长度最长?( )
A.CF B.FD C.BE D.EC
9.如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A. B. C. D.
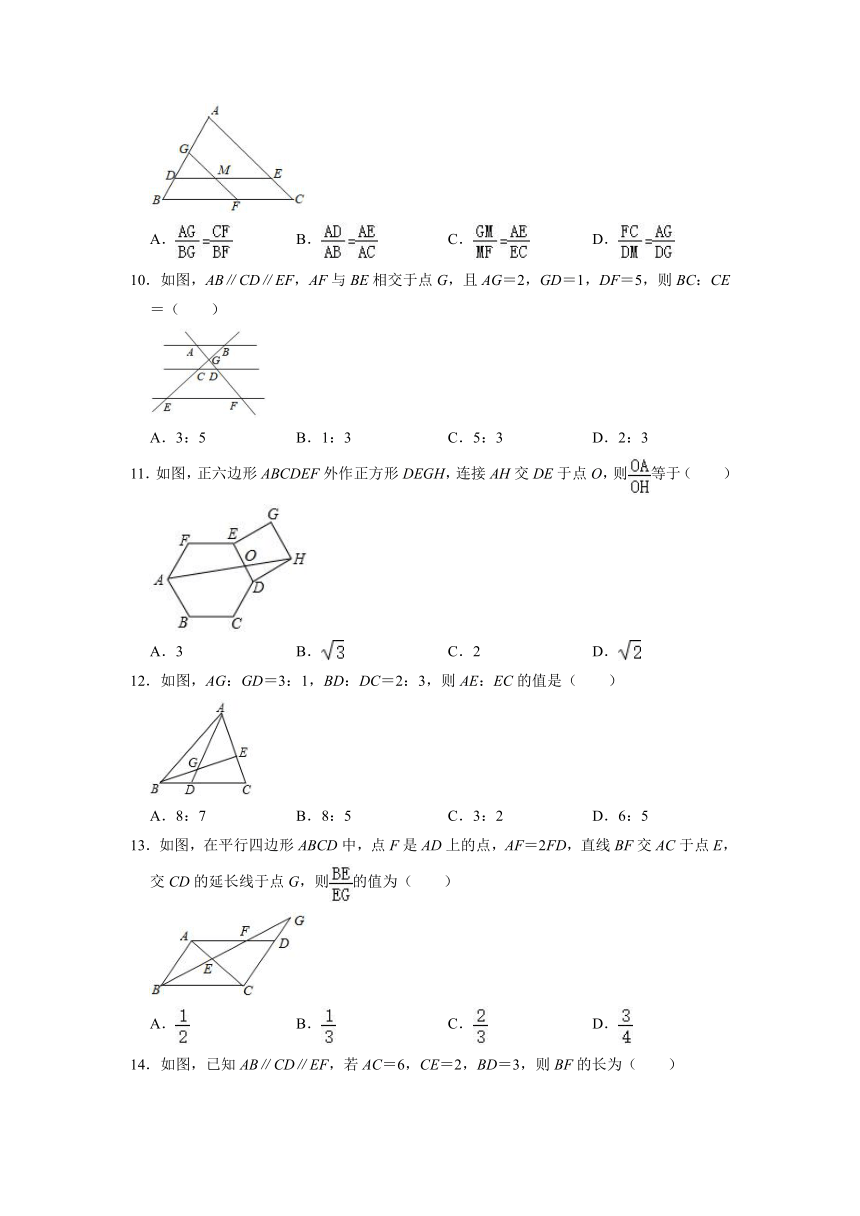
10.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5 B.1:3 C.5:3 D.2:3
11.如图,正六边形ABCDEF外作正方形DEGH,连接AH交DE于点O,则等于( )
A.3 B. C.2 D.
12.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
13.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
14.如图,已知AB∥CD∥EF,若AC=6,CE=2,BD=3,则BF的长为( )
A.6 B.5.5 C.4 D.4.5
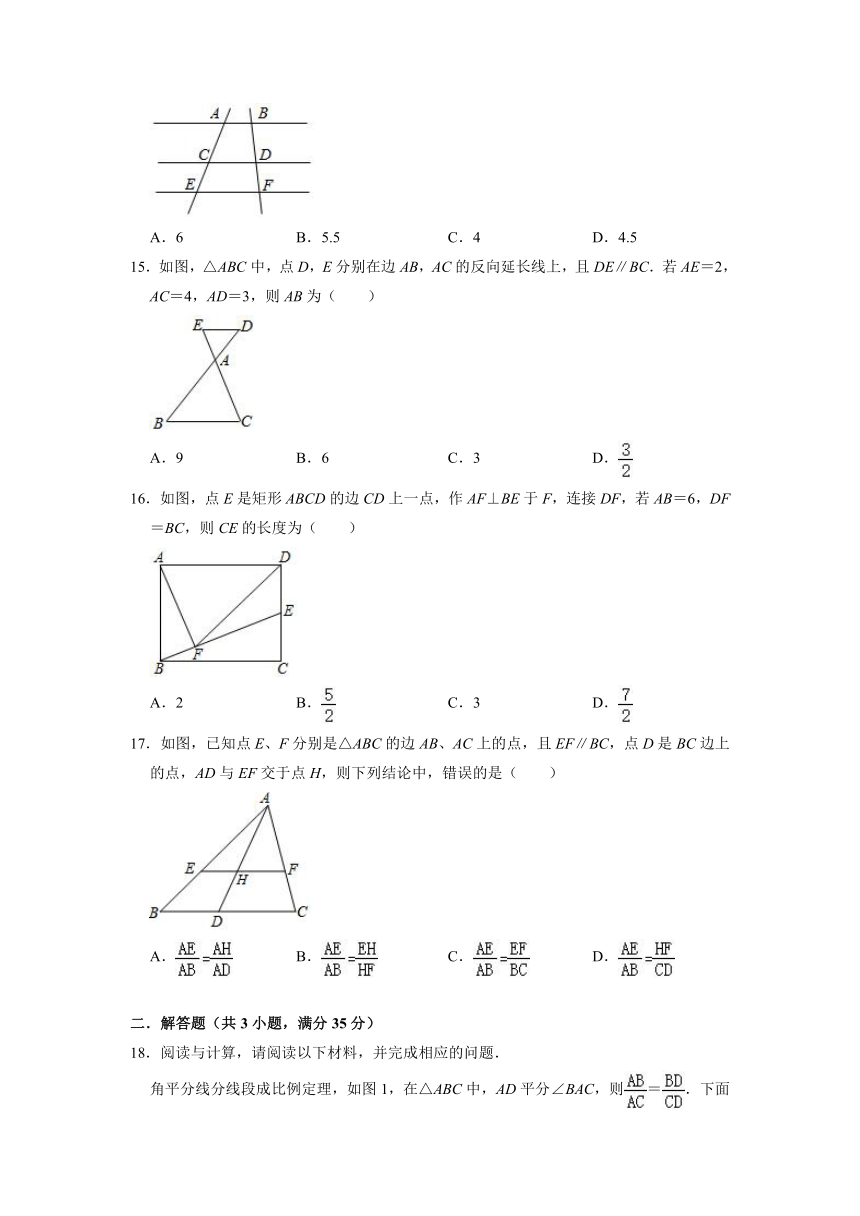
15.如图,△ABC中,点D,E分别在边AB,AC的反向延长线上,且DE∥BC.若AE=2,AC=4,AD=3,则AB为( )
A.9 B.6 C.3 D.
16.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2 B. C.3 D.
17.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
二.解答题(共3小题,满分35分)
18.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
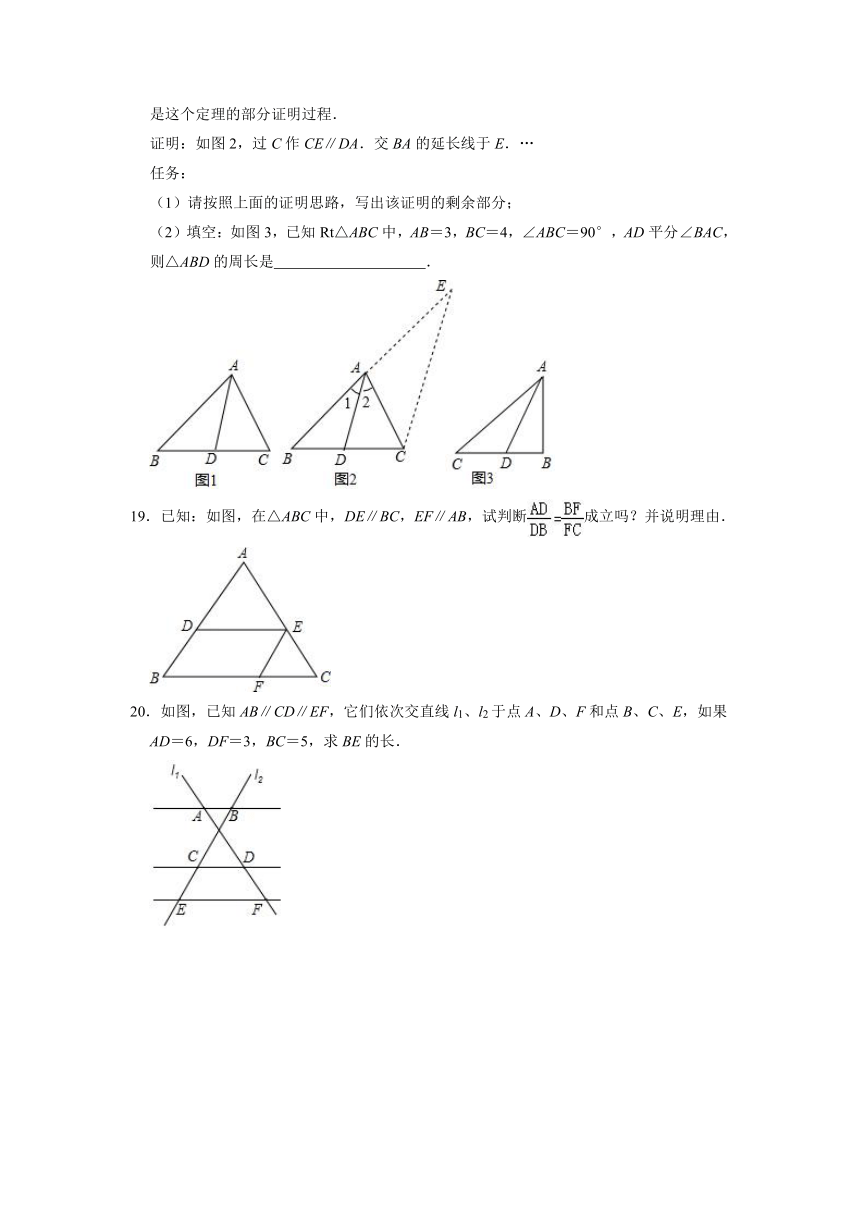
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
19.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
20.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD=6,DF=3,BC=5,求BE的长.
参考答案
一.选择题(共17小题,满分85分)
1.解:∵直线l1∥l2∥l3,
∴=,
∵AB=4,BC=5,EF=4,
∴=,
∴DE=.
故选:B.
2.解:∵DE∥BC,
∴,
∵EF∥AB,
∴,
∴,
故选:B.
3.解:
∵AD=2,AB=6,
∴AD:AB=1:3,
∵AE:AC=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论B不符合题意;
∵AE:EC=1:2,
∴AE:AC=1:(1+2)=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
∵EC:AC=2:3,
∴AE:AC=(3﹣2):3=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
由DE:BC=1:3,得不出DE∥BC,故结论A符合题意;
故选:A.
4.解:∵DE∥BC,
∴=,
∴=,
∴AC=9,
∴EC=AC﹣AE=9﹣6=3,
故选:C.
5.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
6.解:过E点作EH∥BC交AD于H,如图,
∵F为BE中点,
∴EF=BF,
∵HE∥BD,
∴==1,即BD=EH,
∵HE∥CD,
∴=,
∵=,
∴==,
∴=,即CD=3HE,
∴==.
故选:B.
7.解:∵AC∥EF,
∴,
∵EF∥DB,
∴,
∴=+===1,即=1,
∴.
故选:C.
8.解:∵AH=8,HG=5,GD=4,
∴AD=8+5+4=17,
∵四边形ABCD为菱形,
∴BC=CD=AD=17,
∵AE∥HC,AD∥BC,
∴四边形AECH为平行四边形,
∴CE=AH=8,
∴BE=BC﹣CE=17﹣8=9,
∵HC∥GF,
∴=,即=,
解得:DF=,
∴FC=17﹣=,
∵>9>8>,
∴CF长度最长,
故选:A.
9.解:∵DE∥BC,GF∥AC,
∴四边形MECF是平行四边形.
∴=,=,=,ME=FC.
∴=.
所以ABD正确,C错误.
故选:C.
10.解:∵AB∥CD∥EF,
∴===.
故选:A.
11.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∵OD∥AB,
∴===,
故选:B.
12.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
13.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
14.解:∵AB∥CD∥EF,
∴=,即=,
∴BF=4.
故选:C.
15.解:∵点D,E分别在边AB,AC的反向延长线上,且DE∥BC,
∴=,即,
解得AB=6,
故选:B.
16.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
17.解:∵EF∥BC,
∴=,=,==,
∴选项A,C,D正确,
故选:B.
二.解答题(共3小题,满分35分)
18.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
19.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
20.解:∵AB∥CD∥EF,
∴,
即,
解得CE=2.5,
∴BE=BC+CE=5+2.5=7.5.
同步能力达标测评(附答案)
一.选择题(共17小题,满分85分)
1.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=4,BC=5,EF=4,那么DE的长是( )
A. B. C.3 D.
2.如图,在△ABC中,点D,E、F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列式于一定正确的是( )
A. B. C. D.
3.在△ABC中,点D、E分别在边AB、AC上,AD=2,AB=6,那么下列各条件中,不—定能判定DE∥BC的是( )
A. B. C. D.
4.如图,已知点D为△ABC边AB上一点,AD:AB=2:3,过点D作BC的平行线交AC于点E,若AE=6,则EC的长度是( )
A.1 B.2 C.3 D.4
5.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
6.在△ABC中,点E在AC上,且,F为BE中点,AF的延长线交BC于D,则:=( )
A.1:2 B.1:3 C.1:4 D.2:3
7.如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.+= B.+= C.+= D.+=
8.如图,菱形ABCD中,E点在BC上,F点在CD上,G点、H点在AD上,且AE∥HC∥GF.若AH=8,HG=5,GD=4,则下列选项中的线段,何者长度最长?( )
A.CF B.FD C.BE D.EC
9.如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A. B. C. D.
10.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5 B.1:3 C.5:3 D.2:3
11.如图,正六边形ABCDEF外作正方形DEGH,连接AH交DE于点O,则等于( )
A.3 B. C.2 D.
12.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
13.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
14.如图,已知AB∥CD∥EF,若AC=6,CE=2,BD=3,则BF的长为( )
A.6 B.5.5 C.4 D.4.5
15.如图,△ABC中,点D,E分别在边AB,AC的反向延长线上,且DE∥BC.若AE=2,AC=4,AD=3,则AB为( )
A.9 B.6 C.3 D.
16.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2 B. C.3 D.
17.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
二.解答题(共3小题,满分35分)
18.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
19.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
20.如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD=6,DF=3,BC=5,求BE的长.
参考答案
一.选择题(共17小题,满分85分)
1.解:∵直线l1∥l2∥l3,
∴=,
∵AB=4,BC=5,EF=4,
∴=,
∴DE=.
故选:B.
2.解:∵DE∥BC,
∴,
∵EF∥AB,
∴,
∴,
故选:B.
3.解:
∵AD=2,AB=6,
∴AD:AB=1:3,
∵AE:AC=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论B不符合题意;
∵AE:EC=1:2,
∴AE:AC=1:(1+2)=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
∵EC:AC=2:3,
∴AE:AC=(3﹣2):3=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
由DE:BC=1:3,得不出DE∥BC,故结论A符合题意;
故选:A.
4.解:∵DE∥BC,
∴=,
∴=,
∴AC=9,
∴EC=AC﹣AE=9﹣6=3,
故选:C.
5.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
6.解:过E点作EH∥BC交AD于H,如图,
∵F为BE中点,
∴EF=BF,
∵HE∥BD,
∴==1,即BD=EH,
∵HE∥CD,
∴=,
∵=,
∴==,
∴=,即CD=3HE,
∴==.
故选:B.
7.解:∵AC∥EF,
∴,
∵EF∥DB,
∴,
∴=+===1,即=1,
∴.
故选:C.
8.解:∵AH=8,HG=5,GD=4,
∴AD=8+5+4=17,
∵四边形ABCD为菱形,
∴BC=CD=AD=17,
∵AE∥HC,AD∥BC,
∴四边形AECH为平行四边形,
∴CE=AH=8,
∴BE=BC﹣CE=17﹣8=9,
∵HC∥GF,
∴=,即=,
解得:DF=,
∴FC=17﹣=,
∵>9>8>,
∴CF长度最长,
故选:A.
9.解:∵DE∥BC,GF∥AC,
∴四边形MECF是平行四边形.
∴=,=,=,ME=FC.
∴=.
所以ABD正确,C错误.
故选:C.
10.解:∵AB∥CD∥EF,
∴===.
故选:A.
11.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∵OD∥AB,
∴===,
故选:B.
12.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
13.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
14.解:∵AB∥CD∥EF,
∴=,即=,
∴BF=4.
故选:C.
15.解:∵点D,E分别在边AB,AC的反向延长线上,且DE∥BC,
∴=,即,
解得AB=6,
故选:B.
16.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
17.解:∵EF∥BC,
∴=,=,==,
∴选项A,C,D正确,
故选:B.
二.解答题(共3小题,满分35分)
18.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
19.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
20.解:∵AB∥CD∥EF,
∴,
即,
解得CE=2.5,
∴BE=BC+CE=5+2.5=7.5.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
