直线和圆的位置关系复习

(共29张PPT)
直线和圆的位置关系复习课
七十九中学
曾环环
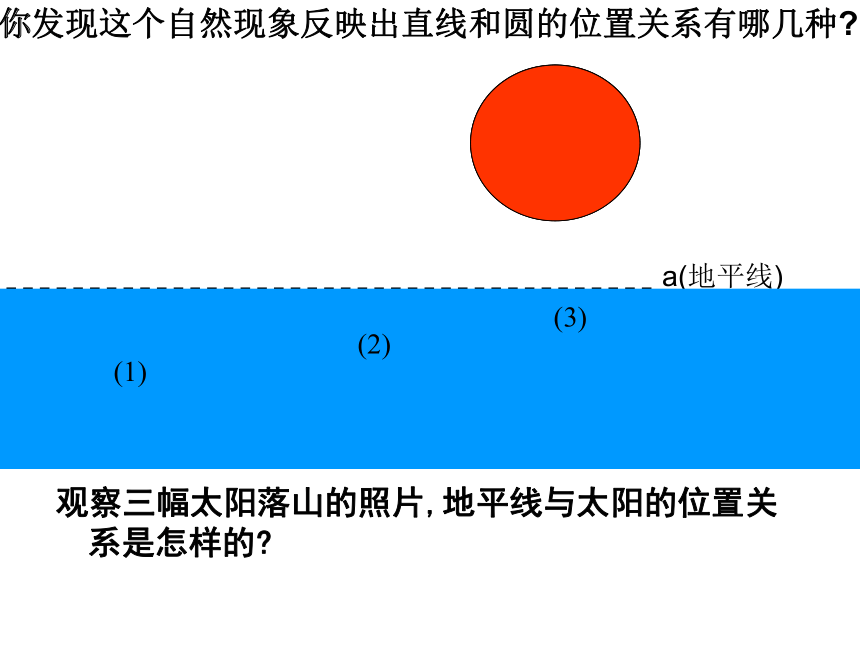
、“大漠孤烟直，长河落日圆” 是唐朝诗人王维的诗句，它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆，地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下，直线和圆的位置关系有几种？
观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
a(地平线)
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(1)
(3)
(2)
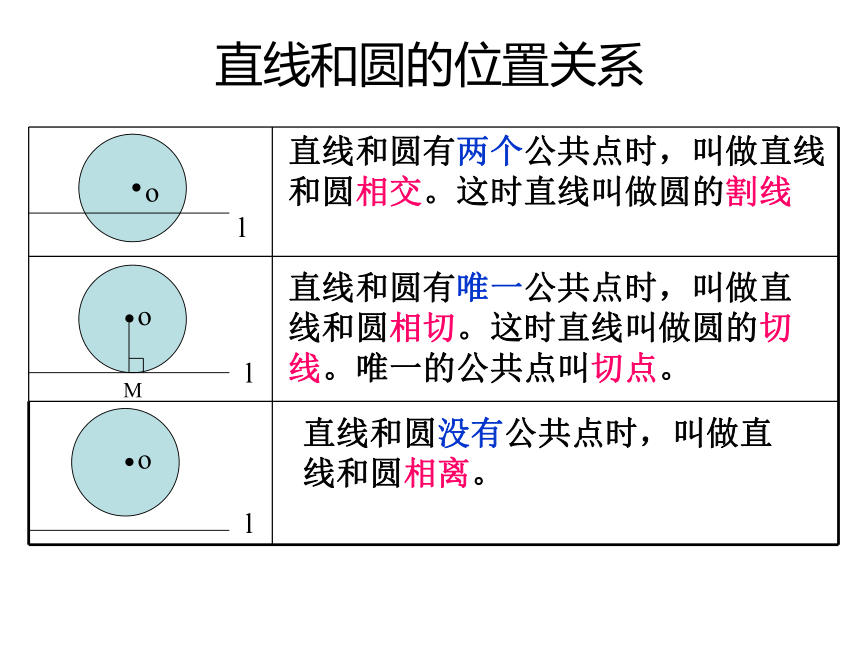
直线和圆的位置关系
l
l
l



直线和圆有两个公共点时，叫做直线和圆相交。这时直线叫做圆的割线
直线和圆有唯一公共点时，叫做直线和圆相切。这时直线叫做圆的切线。唯一的公共点叫切点。
直线和圆没有公共点时，叫做直线和圆相离。
o
o
o
M
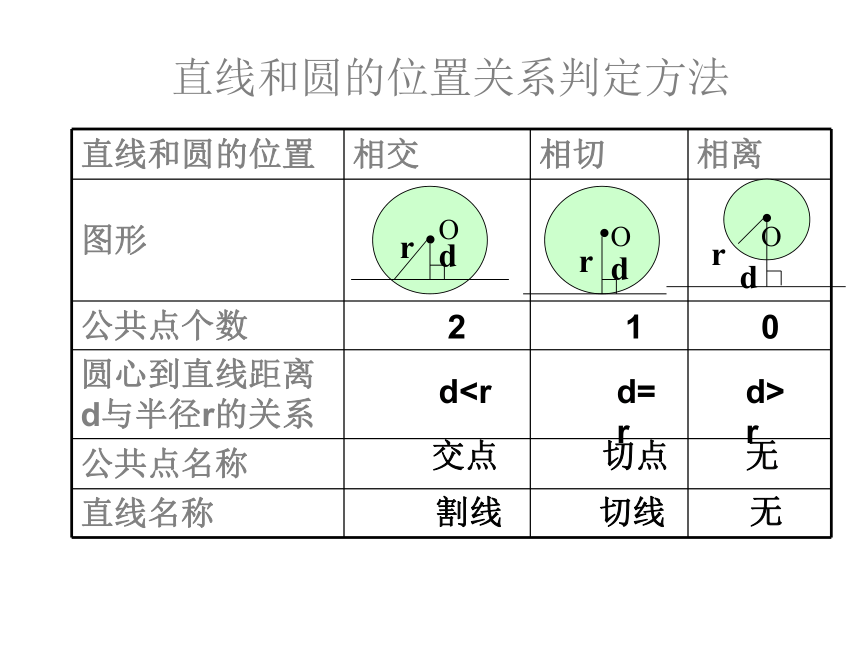
直线和圆的位置关系判定方法
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O

d
r
O
l

d
r
O

d
r
下雨天当你快速转动雨伞时飞出的水，在砂轮上打磨工件飞 出的火星，都是沿着圆的切线的方向飞出的．
问题：1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向？
2 砂轮打磨工件飞出火星的方向是什么方向？
小结：
1、如何判定一条直线是已知圆的切线？
(1)和圆只有一个公共点的直线是圆的切线；
(2)和圆心的距离等于半径的直线是圆的切线；
(3)过半径外端并且和半径垂直的直线是圆的切线；
(d=r)
A 、经过圆上的一点；
B、 垂直于半径；
切线的性质：
1、经过切点的半径垂直与圆的切线
２、经过切点垂直于切线的直线必经过圆心.
A
B
O
T
例１　已知 的斜边AB=6cm,直角AC=3cm,以点C为圆心，半径分别为２cm和4cm画两个圆，这两个圆与AB有怎样的位置关系？当半径为多长时，AB与圆C相切？
A
B
C
D
解析：利用d和r的大小关系判断直线与圆的位置
关系时，关键是准确确定d和r，利用面积法求斜边
上的高是一种常用方法．
　
例2：已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD．求证：DC是⊙O的切线．
分析：要证DC是⊙O的切线，需证DC垂直于过切点的直径或半径，因此要作辅助线半径OD，利用平行关系推出∠3＝∠4，又因为OD＝OB，OC为公共边，因此△CDO≌△CBO，所以∠ODC＝∠OBC＝90°．
证明：连结OD．
∵OA＝OD，∴∠1＝∠2，
∵AD∥OC，∴∠1＝∠3，∠2＝∠4．
∴∠3＝∠4．
∵OD＝OB，OC＝OC，
∴△ODC≌△OBC．
∴∠ODC＝∠OBC．
∵BC是⊙O的切线，
∴∠OBC＝90°．
∴∠ODC＝90°．
∴DC是⊙O的切线．
C
B
A
D
O
1
2
3
4
例3：设c线段AB的中点，四边形BCDE是以BC为一边的正方形。作以B为圆心，BD长为半径的圆B,连接AD。求证：AD是圆B的切线
证明：连接BD.
D
C
B
E
A
规律总结:
证明一条直线是圆的切线,常常要添加辅助线,如果直线与圆有一个公共点,则连接这点和圆心,证明直线垂直于经过这点的半径.
练一练
1、如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD＝∠B＝30°，边BD交圆于点D。BD是⊙O的切线吗？为什么？
解：BD是⊙O的切线 。连结OD。
又∵∠B＋∠BOD＋∠BDO ＝ 180°
∵ OA＝OD ， ∠BAD＝30°(已知)
∴ 直线BD⊥OD
又∵直线BD 经过⊙O上的D点
∴直线BD是⊙O的切线
∴∠ODA＝∠A＝30°(等边对等角)
∴∠BOD＝∠A＋∠ODA＝60°
O
●
A
B
C
D
∴∠BDO＝180°－∠B－∠BOD＝90°
A
B
D
O
C
E
规律总结：
证明一条直线是圆的切线，如果直线与圆的公共点没有确定，则应过圆心作直线的垂线段，然后证明这条线段等于这个圆的半径。
这道题综合运用了切线的性质定理和判定定理。欲证是圆0的切线，根据条件，采用“做垂线段证半径”法。
A
B
C
E
D
O
练习3：如右图所示，已知OC平分∠AOB，D是OC上任意一点，⊙D与OA相切于点E。那么，OB是⊙D的切线吗？请说明理由。
练一练
E
C
D
●
解：OB是⊙D的切线 。理由如下：
又∵ OC平分∠AOB， DF⊥OB
∴ DF ＝ DE
∴ OB是⊙D的切线 。
∴ OE⊥OA
∵ OA 与⊙D 相切于点E
连结DE，过D点作DF⊥OB，垂足为F。
A
B
O
F
┐
即 d ＝ r
练习4:如图，台风中心P（100，200）沿北偏东30O方向移动，受台风影响区域的半径为200km，那么下列城市A（200，380），B（600，480），C（550，300），D（370，540）中，哪些城市要做抗台风准备？
如图，台风中心P（100，200）沿北偏东30O方向移动，受台风影响区域的半径为200km，那么下列城市A（200，380），B（600，480），C（550，300），D（370，540）中，哪些城市要做抗台风准备？
P
A
B
C
D
练习:如图，直角梯形ABCD，AD∥BC，∠ADC＝135°，DC＝8
以D为圆心，以8个单位长为半径作⊙D，试判定⊙D与BC有向几个交点？
分析：⊙D与BC交点的个数，决定于点D到BC的距离，作DE⊥BC于E，计算DE的长度，即可作出判断。
解：作DE⊥BC于E　∵AD∥BC 　　　　 ∴∠ADC＋∠C＝180° 　　　　 又∠ADC＝135°，∴∠C＝45° 　　　　 ∴△DEC为等腰直角三角形 　　　　 ∵CD＝8
　　　　 ∴DE＝8，即点D到BC的距离是8个单位， 　　　　 因此⊙D与BC只有一个交点。
1 今天我们一起复习哪些圆的有关知识？
2 今天我们探究的问题都有什么特点？
3 今天你有什么收获吗？
作业：
书上Ｐ１１５页，２、３
再见