2021秋北师版九上数学1.1菱形的性质与判定课件(两课时,共35张PPT)
文档属性
| 名称 | 2021秋北师版九上数学1.1菱形的性质与判定课件(两课时,共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
1 菱形的性质与判定
第1课时 菱形及其性质
学校:________
教师:________
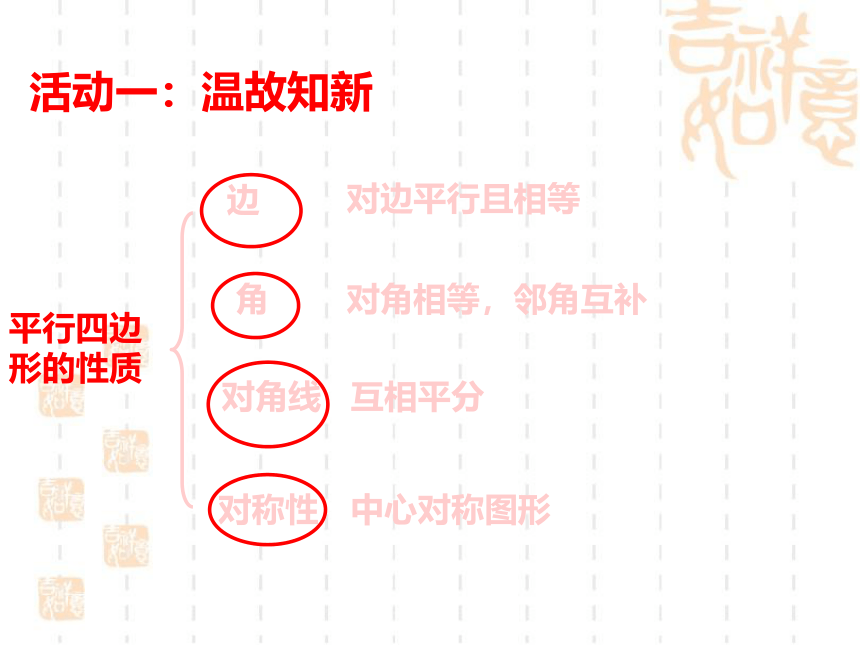
平行四边形的性质
边
角
对称性
活动一:温故知新
对角线
对边平行且相等
对角相等,邻角互补
互相平分
中心对称图形
活动二:观 察
下面的平行四边形中,有什么共同的特征吗?
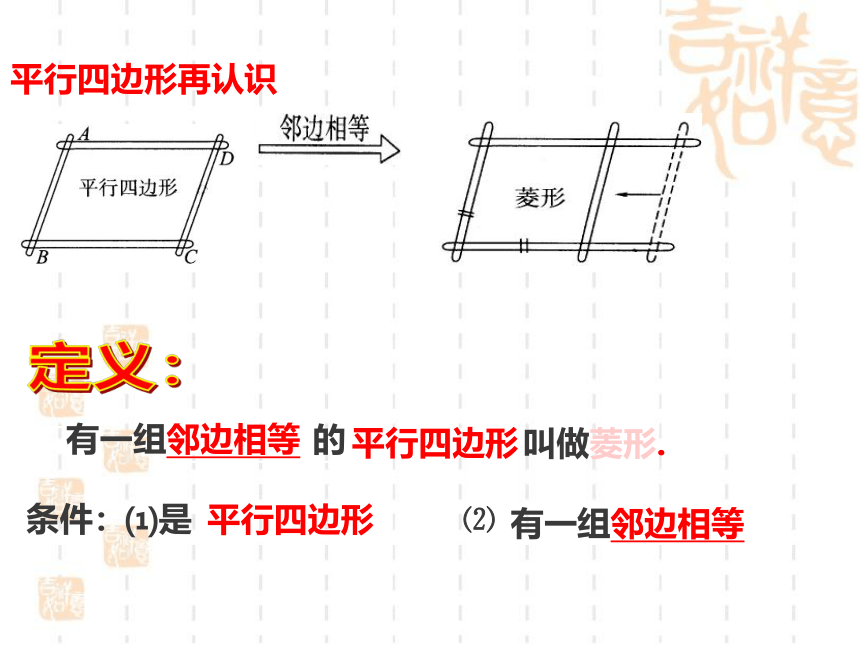
有一组邻边相 平行四边形叫做菱形.
条件:
⑴是 ;
⑵ .
平行四边形
平行四边形
有一组邻边相等
有一组邻边相等
平行四边形再认识
的
感受生活
你还能举出生活中你看到的菱形吗?
菱形是特殊的平行四边形,它具有平行四边形的一切性质.即
菱形的对边平行且相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形是中心对称图形,对角线的
交点是对称中心.
菱形具有一般平行四边形的所有性质吗?
A
B
C
D
O
菱形具有哪些特殊性质?用菱形纸片折一折.
菱形的四条边都相等
菱形是轴对称图形吗?如果是,它
有几条对称轴?对称轴之间有什么位置关系?
菱形中有哪些相等的线段?
菱形是轴对称图形,它有两条对称轴,对称轴互相垂直.菱形的两条对角线互相垂直.
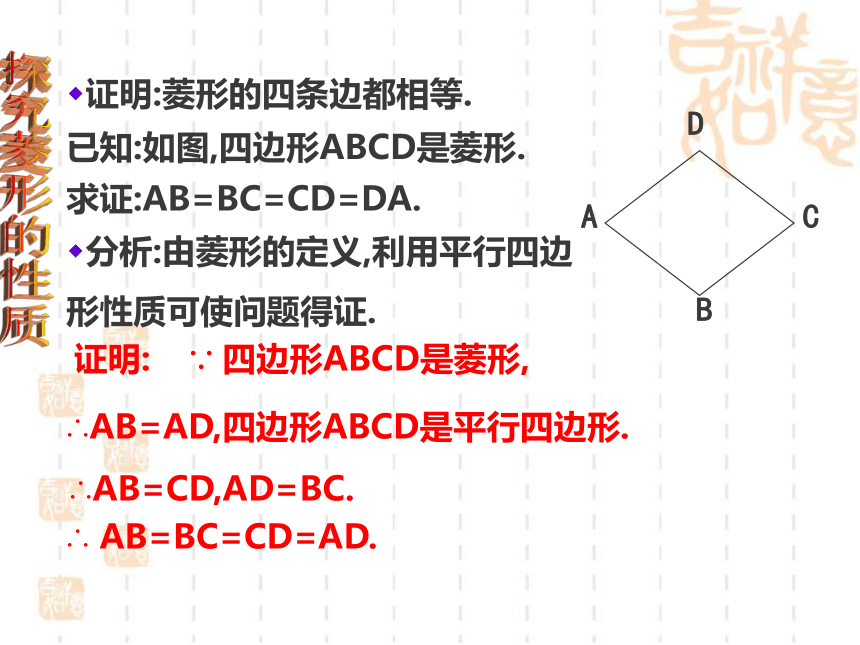
证明:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
证明:
∵ 四边形ABCD是菱形,
∴AB=AD,四边形ABCD是平行四边形.
∴AB=CD,AD=BC.
求证:AB=BC=CD=DA.
∴ AB=BC=CD=AD.
C
B
D
A
分析:由菱形的定义,利用平行四边形性质可使问题得证.
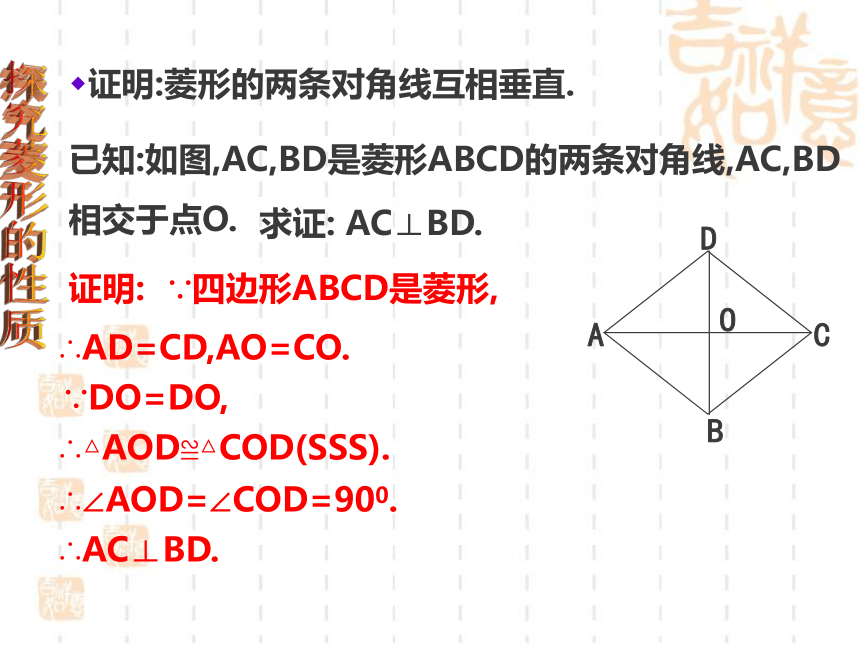
证明:菱形的两条对角线互相垂直.
已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.
求证: AC⊥BD.
证明:
∵四边形ABCD是菱形,
∴AD=CD,AO=CO.
∵DO=DO,
∴△AOD≌△COD(SSS).
∴∠AOD=∠COD=900.
D
B
C
A
O
∴AC⊥BD.
D
B
C
A
O
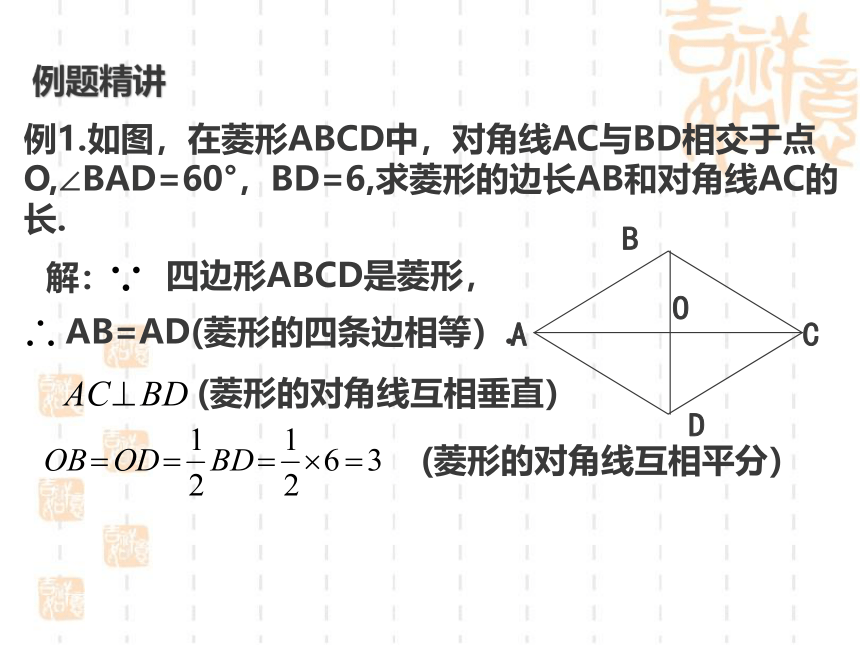
例题精讲
例1.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=6,求菱形的边长AB和对角线AC的长.
解:
四边形ABCD是菱形,
AB=AD(菱形的四条边相等).
(菱形的对角线互相垂直)
(菱形的对角线互相平分)
在等腰三角形ABD中,
(菱形的对角线互相平分).
一展身手
1.菱形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 两组对角分别相等
C 对角线互相平分 D 对角线互相垂直
D
2.已知菱形的周长是12cm,那么它的边长是______.
3cm
3.菱形ABCD中,O是两条对角线的交点,已知AC=8cm,DB=6cm,求AB的长.
C
B
D
A
O
1个定义
3个特性
:有一组邻边相等的平行四边形叫菱形
:特在“边、对角线、对称性”
1 菱形的性质与判定
第2课时 菱形的判定
学校:________
教师:________
有一组邻边相等的平行四边形叫做菱形.
3.菱形的性质:
1.菱形的定义:
(A)菱形的四条边都相等
(B)菱形的对角线互相垂直平分
2.菱形的特征:
菱形是一个轴对称图形
我们可以根据定义来判定一个四边形是菱形.除此之外,还能找到其他的判定方法吗?
菱形的性质“两条对角线互相垂直平分”中,“对角线互相平分”是平行四边形所具有的一般性质,而“对角线垂直”是菱形所特有的性质.
由此,可以得到一个猜想:“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是一个菱形.”
已知:如图,平行四边形ABCD中,对角线AC、BD互相垂直.求证: 四边形ABCD是菱形.
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC
又∵AC⊥BD
∴ BD所在直线是线段AC的垂直平分线
∴ AB=BC
∴ 四边形ABCD是菱形
对于一个一般的四边形,能否也可以找到判定它是不是菱形的方法呢?由菱形的另一条性质“四条边都相等”,
你可能会想到: 如果一个四边形的四条边都相等,那它会不会一定是菱形?试着画一画,与周围的同学讨论,猜一猜结论是否成立.
由此我们得到了判定菱形的又一种方法:
四条边都相等的四边形是菱形.
菱形的判定方法
1.有一组邻边相等的平行四边形是菱形
3.四条边都相等的四边形是菱形
2.对角线互相垂直的平行四边形是菱形
1.下列条件中,不能判定四边形ABCD为菱形的是( )
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BD
O
A
D
C
B
C
2.已知:如图,在平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF//AB,与AD相交于点F.
求证:四边形ABEF是菱形.
A
B
C
D
E
F
3.已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC.
求证:四边形CDEF是菱形
O
1
2
A
C
B
D
E
F
4.已知:如图,在正方形ABCD中,点E、F在BD上,且BF=DE.
求证:四边形AECF是菱形.
A
D
C
B
F
E
O
你能说出这节课的心得和体会, 让大家与你分享吗?
菱形的性质与判定(3)
菱形的性质
驶向胜利的彼岸
定理:菱形的四条边都相等.
定理:菱形的两条对角线互相垂直,并且每条对角线平分一组对角.
回顾 思考
∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵AC,BD是菱形ABCD的两条对角线.
∴AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC.
C
B
D
A
D
B
C
A
O
菱形的判定
驶向胜利的彼岸
定理:四条边都相等的四边形是菱形.
定理:对角线互相垂直的平行四边形是菱形.
回顾 思考
在四边形ABCD中,
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
∵AC,BD是□ABCD的两条对角线,AC⊥BD.
∴四边形ABCD是菱形.
C
B
D
A
D
B
C
A
O
如图,平行四边形的两条对角线AC,
BD相交于点O,AB= , AO=2,OB=1.
(1) AC,BD互相垂直吗?为什么?
A
B
C
D
O
2
1
(2) 四边形 ABCD是菱形吗?为什么?
试一试
菱形性质的应用
例题解析
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度;
(2).菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
菱形的面积等于两条对角线乘积的一半
∵ 四边形ABCD是菱形∴ AC⊥BD
解:
思考:
若对角线AC的长度为m,BD的长度为n,则菱形ABCD的面积是多少?
∴菱形ABCD的面积=4 × △AOB=4 ×6=24
∴ AO= AC= ×8=4cm,BO=3cm ,
= ×4×3=6
∴△AOB的面积= ×AO ×BO
在菱形ABCD中,对角线AC=8cm,BD=6cm,问菱形ABCD的面积是多少?
思考
A
B
D
C
O
试一试
如图,两张等宽的纸条交重叠在一起,重叠的部分ABCD是菱形吗?为什么?
A
D
C
B
菱形的四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角.
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
菱形的性质:
菱形的判别方式:
本课小结
P9 练习1.3
作 业
1 菱形的性质与判定
第1课时 菱形及其性质
学校:________
教师:________
平行四边形的性质
边
角
对称性
活动一:温故知新
对角线
对边平行且相等
对角相等,邻角互补
互相平分
中心对称图形
活动二:观 察
下面的平行四边形中,有什么共同的特征吗?
有一组邻边相 平行四边形叫做菱形.
条件:
⑴是 ;
⑵ .
平行四边形
平行四边形
有一组邻边相等
有一组邻边相等
平行四边形再认识
的
感受生活
你还能举出生活中你看到的菱形吗?
菱形是特殊的平行四边形,它具有平行四边形的一切性质.即
菱形的对边平行且相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形是中心对称图形,对角线的
交点是对称中心.
菱形具有一般平行四边形的所有性质吗?
A
B
C
D
O
菱形具有哪些特殊性质?用菱形纸片折一折.
菱形的四条边都相等
菱形是轴对称图形吗?如果是,它
有几条对称轴?对称轴之间有什么位置关系?
菱形中有哪些相等的线段?
菱形是轴对称图形,它有两条对称轴,对称轴互相垂直.菱形的两条对角线互相垂直.
证明:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
证明:
∵ 四边形ABCD是菱形,
∴AB=AD,四边形ABCD是平行四边形.
∴AB=CD,AD=BC.
求证:AB=BC=CD=DA.
∴ AB=BC=CD=AD.
C
B
D
A
分析:由菱形的定义,利用平行四边形性质可使问题得证.
证明:菱形的两条对角线互相垂直.
已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.
求证: AC⊥BD.
证明:
∵四边形ABCD是菱形,
∴AD=CD,AO=CO.
∵DO=DO,
∴△AOD≌△COD(SSS).
∴∠AOD=∠COD=900.
D
B
C
A
O
∴AC⊥BD.
D
B
C
A
O
例题精讲
例1.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD=6,求菱形的边长AB和对角线AC的长.
解:
四边形ABCD是菱形,
AB=AD(菱形的四条边相等).
(菱形的对角线互相垂直)
(菱形的对角线互相平分)
在等腰三角形ABD中,
(菱形的对角线互相平分).
一展身手
1.菱形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 两组对角分别相等
C 对角线互相平分 D 对角线互相垂直
D
2.已知菱形的周长是12cm,那么它的边长是______.
3cm
3.菱形ABCD中,O是两条对角线的交点,已知AC=8cm,DB=6cm,求AB的长.
C
B
D
A
O
1个定义
3个特性
:有一组邻边相等的平行四边形叫菱形
:特在“边、对角线、对称性”
1 菱形的性质与判定
第2课时 菱形的判定
学校:________
教师:________
有一组邻边相等的平行四边形叫做菱形.
3.菱形的性质:
1.菱形的定义:
(A)菱形的四条边都相等
(B)菱形的对角线互相垂直平分
2.菱形的特征:
菱形是一个轴对称图形
我们可以根据定义来判定一个四边形是菱形.除此之外,还能找到其他的判定方法吗?
菱形的性质“两条对角线互相垂直平分”中,“对角线互相平分”是平行四边形所具有的一般性质,而“对角线垂直”是菱形所特有的性质.
由此,可以得到一个猜想:“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是一个菱形.”
已知:如图,平行四边形ABCD中,对角线AC、BD互相垂直.求证: 四边形ABCD是菱形.
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC
又∵AC⊥BD
∴ BD所在直线是线段AC的垂直平分线
∴ AB=BC
∴ 四边形ABCD是菱形
对于一个一般的四边形,能否也可以找到判定它是不是菱形的方法呢?由菱形的另一条性质“四条边都相等”,
你可能会想到: 如果一个四边形的四条边都相等,那它会不会一定是菱形?试着画一画,与周围的同学讨论,猜一猜结论是否成立.
由此我们得到了判定菱形的又一种方法:
四条边都相等的四边形是菱形.
菱形的判定方法
1.有一组邻边相等的平行四边形是菱形
3.四条边都相等的四边形是菱形
2.对角线互相垂直的平行四边形是菱形
1.下列条件中,不能判定四边形ABCD为菱形的是( )
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BD
O
A
D
C
B
C
2.已知:如图,在平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF//AB,与AD相交于点F.
求证:四边形ABEF是菱形.
A
B
C
D
E
F
3.已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC.
求证:四边形CDEF是菱形
O
1
2
A
C
B
D
E
F
4.已知:如图,在正方形ABCD中,点E、F在BD上,且BF=DE.
求证:四边形AECF是菱形.
A
D
C
B
F
E
O
你能说出这节课的心得和体会, 让大家与你分享吗?
菱形的性质与判定(3)
菱形的性质
驶向胜利的彼岸
定理:菱形的四条边都相等.
定理:菱形的两条对角线互相垂直,并且每条对角线平分一组对角.
回顾 思考
∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵AC,BD是菱形ABCD的两条对角线.
∴AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC.
C
B
D
A
D
B
C
A
O
菱形的判定
驶向胜利的彼岸
定理:四条边都相等的四边形是菱形.
定理:对角线互相垂直的平行四边形是菱形.
回顾 思考
在四边形ABCD中,
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
∵AC,BD是□ABCD的两条对角线,AC⊥BD.
∴四边形ABCD是菱形.
C
B
D
A
D
B
C
A
O
如图,平行四边形的两条对角线AC,
BD相交于点O,AB= , AO=2,OB=1.
(1) AC,BD互相垂直吗?为什么?
A
B
C
D
O
2
1
(2) 四边形 ABCD是菱形吗?为什么?
试一试
菱形性质的应用
例题解析
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度;
(2).菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
菱形的面积等于两条对角线乘积的一半
∵ 四边形ABCD是菱形∴ AC⊥BD
解:
思考:
若对角线AC的长度为m,BD的长度为n,则菱形ABCD的面积是多少?
∴菱形ABCD的面积=4 × △AOB=4 ×6=24
∴ AO= AC= ×8=4cm,BO=3cm ,
= ×4×3=6
∴△AOB的面积= ×AO ×BO
在菱形ABCD中,对角线AC=8cm,BD=6cm,问菱形ABCD的面积是多少?
思考
A
B
D
C
O
试一试
如图,两张等宽的纸条交重叠在一起,重叠的部分ABCD是菱形吗?为什么?
A
D
C
B
菱形的四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角.
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
菱形的性质:
菱形的判别方式:
本课小结
P9 练习1.3
作 业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
