2021-2022学年人教版数学七年级上册3.2 解一元一次方程(一)——合并同类项与移项课件(第1课时 30张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册3.2 解一元一次方程(一)——合并同类项与移项课件(第1课时 30张) |  | |
| 格式 | zip | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 14:25:00 | ||
图片预览









文档简介
(共30张PPT)
3.2 解一元一次方程(一)
——合并同类项与移项
人教版· 数学· 七年级(上)
第三章 一元一次方程
第1课时 利用合并同类项解一元一次方程
学会运用合并同类项解形如ax+bx=c类型的一元一次方程,进一步体会方程中的“化归”思想。
学习目标
约公元820年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.
对消,顾名思义,就是将方程中各项成对消除的意思.相当于解方程中的“合并同类项”.
导入新知
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
设前年购买计算机 x 台.
可以表示出:去年购买计算机 2x 台,今年购买计算机 4x 台.
根据问题中的相等关系:前年购买量+去年购买量 + 今年购买量=140台,
列得方程 x+2x+4x= 140.
新知 解一元一次方程——合并同类项
今年是前年的几倍呢?
这个方程怎么解呢?
合作探究
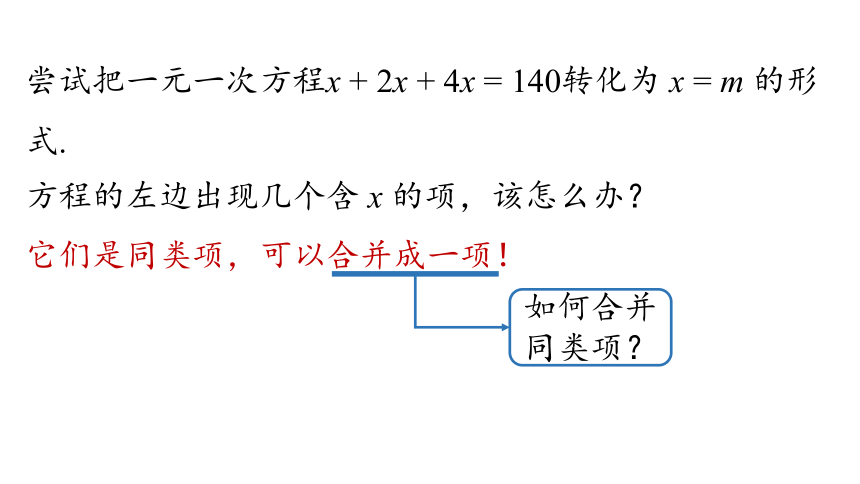
尝试把一元一次方程x + 2x + 4x = 140转化为 x = m 的形式.
方程的左边出现几个含 x 的项,该怎么办?
它们是同类项,可以合并成一项!
如何合并同类项?
合并同类项
系数化为1
依据:分配律
依据:等式的性质2
用合并同类项解一元一次方程的步骤:
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为 ax=b(a≠0)的形式;
第二步:系数化为1,即在方程两边同时除以未知数的系数(或乘未知数系数的倒数),将未知数的系数化为1,得到 x=(a≠0).
上述解方程中的“合并”起了什么作用?
解方程中“合并”起了化简作用,把含有未知数的项合并为一项,从而达到把方程转化为ax = b的形式,其中a,b是常数且a≠0,“合并”的依据是分配律.
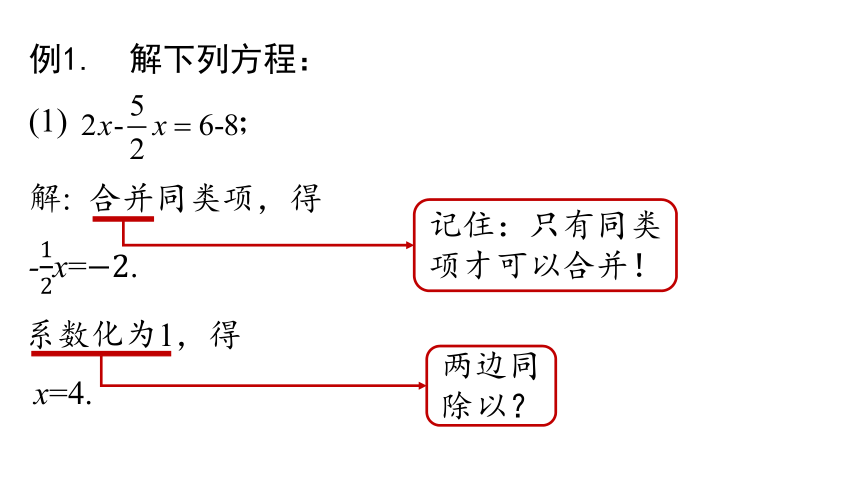
解: 合并同类项,得
系数化为1,得
例1. 解下列方程:
(1) ;
-x=.
x=4.
两边同除以?
记住:只有同类项才可以合并!
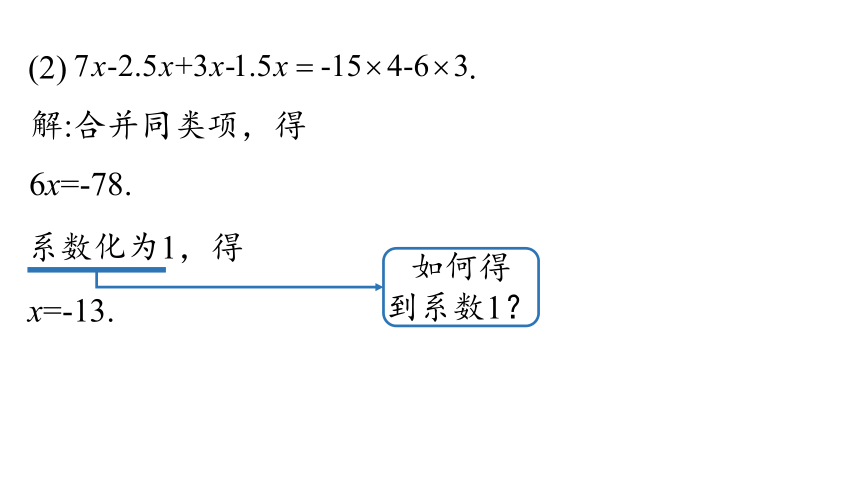
(2) .
解:合并同类项,得
6x=-78.
系数化为1,得
x=-13.
如何得到系数1?
解方程中的合并同类项与整式加减中的合并同类项一样,要牢记合并同类项法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
注意:系数为1或 -1的项在合并时不能漏掉.
解方程: .
解:合并同类项,得
,
系数化为1,得
.
巩固新知
1.解下列方程:
(1) 5x-2x = 9;
解:(1) 合并同类项,得
3x=9,
系数化为1,得
x=3.
(2) .
(2) 合并同类项,得
2x=7,
系数化为1,得
x=.
课堂练习P88
用合并同类项解一元一次方程的步骤:
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为 ax=b(a≠0)的形式;
第二步:系数化为1,即在方程两边同时除以未知数的系数(或乘未知数系数的倒数),将未知数的系数化为1,得到 x=(a≠0).
归纳新知
例2.(教材P87例2变式)按规律排列的一列数:2,-4,8,-16,32,-64,128,-256……其中某四个相邻的数的和是-640,求这四个数中最大数与最小数的差是多少.
解:设这四个相邻的数分别为x,-2x,4x,-8x,
根据题意,得x-2x+4x-8x=-640,解得x=128,
则-2x=-256,4x=512,-8x=-1 024,512-(-1 024)=1 536,
所以这四个数中最大数与最小数的差是1 536.
B
课后练习
2.对于方程4y-2y+y=-1+4,合并同类项正确的是( )
A.2y=3 B.2y=5
C.3y=3 D.3y=-3
3.方程x+2x=-6的解是( )
A.x=0 B.x=1
C.x=2 D.x=-2
C
D
B
5.一个角与它的3倍之和是180°,则这个角是____°.
6.已知2a2xb3x是五次单项式,则x=___.
45
1
解:x=1.
解:x=12.
解:y=6.
8.挖一条长1 210 m的水渠,由甲、乙两队从两头同时施工,
甲队每天挖130 m,乙队每天挖90 m,需几天才能挖好?
设需用x天才能挖好,则所列方程正确的是( )
A.130x+90x=1 210 B.130+90x=1 210
C.130x+90=1 210 D.(130-90)x=1 210
A
9.某人有连续4天的休假,这4天的日期之和是86,
则休假第一天的日期是( )
A.20日 B.21日 C.22日 D.23日
10.三角形的三边长之比为2∶3∶4,其周长为45 cm,
则这个三角形的三边的长分别为____________________.
A
10cm,15cm,20cm
11.随着“垃圾分类”话题的热度居高不下,某市将如何实施城乡垃圾分类工作也倍受市民的关注.根据垃圾分类工作的要求,该市2019年第一季度共生产环保垃圾箱2 800个,第一个月生产量是第二个月的2倍,第三个月生产量是第一个月的2倍,试问第二个月生产环保垃圾箱多少个.
解:设第二个月生产环保垃圾箱x个,依题意有2x+x+2×2x=2 800,
解得x=400.答:第二个月生产环保垃圾箱400个.
C
13.公元前4世纪的印度巴克沙利手稿中记载着一题:甲、乙、丙、丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人持金的总数为132卢比,则乙的持金数为( )
A.4卢比 B.8卢比
C.12卢比 D.16卢比
B
D
15.在等式10×□-3×□=16的两个方格内填入一个相同的数,
则该方格内的数是____.
(3)2.4x-3x-1.4x=5.2-8.
解:合并同类项,得-2x=-2.8.系数化为1,得x=1.4.
17.某人把720 cm长的铁丝分成2段,分别做成两个正方形的数学模型,
已知两个正方形的边长比是4∶5,求这两个正方形的边长分别是多少.
解:设小正方形的边长为4x cm,则大正方形的边长为5x cm,
所以4x·4+5x·4=720,解得x=20.
所以两个正方形的边长分别为4x=4×20=80,5x=5×20=100.
答:这两个正方形的边长分别是80 cm,100 cm.
再
见
3.2 解一元一次方程(一)
——合并同类项与移项
人教版· 数学· 七年级(上)
第三章 一元一次方程
第1课时 利用合并同类项解一元一次方程
学会运用合并同类项解形如ax+bx=c类型的一元一次方程,进一步体会方程中的“化归”思想。
学习目标
约公元820年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.
对消,顾名思义,就是将方程中各项成对消除的意思.相当于解方程中的“合并同类项”.
导入新知
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
设前年购买计算机 x 台.
可以表示出:去年购买计算机 2x 台,今年购买计算机 4x 台.
根据问题中的相等关系:前年购买量+去年购买量 + 今年购买量=140台,
列得方程 x+2x+4x= 140.
新知 解一元一次方程——合并同类项
今年是前年的几倍呢?
这个方程怎么解呢?
合作探究
尝试把一元一次方程x + 2x + 4x = 140转化为 x = m 的形式.
方程的左边出现几个含 x 的项,该怎么办?
它们是同类项,可以合并成一项!
如何合并同类项?
合并同类项
系数化为1
依据:分配律
依据:等式的性质2
用合并同类项解一元一次方程的步骤:
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为 ax=b(a≠0)的形式;
第二步:系数化为1,即在方程两边同时除以未知数的系数(或乘未知数系数的倒数),将未知数的系数化为1,得到 x=(a≠0).
上述解方程中的“合并”起了什么作用?
解方程中“合并”起了化简作用,把含有未知数的项合并为一项,从而达到把方程转化为ax = b的形式,其中a,b是常数且a≠0,“合并”的依据是分配律.
解: 合并同类项,得
系数化为1,得
例1. 解下列方程:
(1) ;
-x=.
x=4.
两边同除以?
记住:只有同类项才可以合并!
(2) .
解:合并同类项,得
6x=-78.
系数化为1,得
x=-13.
如何得到系数1?
解方程中的合并同类项与整式加减中的合并同类项一样,要牢记合并同类项法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
注意:系数为1或 -1的项在合并时不能漏掉.
解方程: .
解:合并同类项,得
,
系数化为1,得
.
巩固新知
1.解下列方程:
(1) 5x-2x = 9;
解:(1) 合并同类项,得
3x=9,
系数化为1,得
x=3.
(2) .
(2) 合并同类项,得
2x=7,
系数化为1,得
x=.
课堂练习P88
用合并同类项解一元一次方程的步骤:
第一步:合并同类项,即将等号同侧的含未知数的项、常数项分别合并,把方程转化为 ax=b(a≠0)的形式;
第二步:系数化为1,即在方程两边同时除以未知数的系数(或乘未知数系数的倒数),将未知数的系数化为1,得到 x=(a≠0).
归纳新知
例2.(教材P87例2变式)按规律排列的一列数:2,-4,8,-16,32,-64,128,-256……其中某四个相邻的数的和是-640,求这四个数中最大数与最小数的差是多少.
解:设这四个相邻的数分别为x,-2x,4x,-8x,
根据题意,得x-2x+4x-8x=-640,解得x=128,
则-2x=-256,4x=512,-8x=-1 024,512-(-1 024)=1 536,
所以这四个数中最大数与最小数的差是1 536.
B
课后练习
2.对于方程4y-2y+y=-1+4,合并同类项正确的是( )
A.2y=3 B.2y=5
C.3y=3 D.3y=-3
3.方程x+2x=-6的解是( )
A.x=0 B.x=1
C.x=2 D.x=-2
C
D
B
5.一个角与它的3倍之和是180°,则这个角是____°.
6.已知2a2xb3x是五次单项式,则x=___.
45
1
解:x=1.
解:x=12.
解:y=6.
8.挖一条长1 210 m的水渠,由甲、乙两队从两头同时施工,
甲队每天挖130 m,乙队每天挖90 m,需几天才能挖好?
设需用x天才能挖好,则所列方程正确的是( )
A.130x+90x=1 210 B.130+90x=1 210
C.130x+90=1 210 D.(130-90)x=1 210
A
9.某人有连续4天的休假,这4天的日期之和是86,
则休假第一天的日期是( )
A.20日 B.21日 C.22日 D.23日
10.三角形的三边长之比为2∶3∶4,其周长为45 cm,
则这个三角形的三边的长分别为____________________.
A
10cm,15cm,20cm
11.随着“垃圾分类”话题的热度居高不下,某市将如何实施城乡垃圾分类工作也倍受市民的关注.根据垃圾分类工作的要求,该市2019年第一季度共生产环保垃圾箱2 800个,第一个月生产量是第二个月的2倍,第三个月生产量是第一个月的2倍,试问第二个月生产环保垃圾箱多少个.
解:设第二个月生产环保垃圾箱x个,依题意有2x+x+2×2x=2 800,
解得x=400.答:第二个月生产环保垃圾箱400个.
C
13.公元前4世纪的印度巴克沙利手稿中记载着一题:甲、乙、丙、丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人持金的总数为132卢比,则乙的持金数为( )
A.4卢比 B.8卢比
C.12卢比 D.16卢比
B
D
15.在等式10×□-3×□=16的两个方格内填入一个相同的数,
则该方格内的数是____.
(3)2.4x-3x-1.4x=5.2-8.
解:合并同类项,得-2x=-2.8.系数化为1,得x=1.4.
17.某人把720 cm长的铁丝分成2段,分别做成两个正方形的数学模型,
已知两个正方形的边长比是4∶5,求这两个正方形的边长分别是多少.
解:设小正方形的边长为4x cm,则大正方形的边长为5x cm,
所以4x·4+5x·4=720,解得x=20.
所以两个正方形的边长分别为4x=4×20=80,5x=5×20=100.
答:这两个正方形的边长分别是80 cm,100 cm.
再
见
