2021-2022学年人教版七年级数学上册 3.1.2等式的性质 课件(35张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 3.1.2等式的性质 课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 875.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 14:27:31 | ||
图片预览




文档简介
(共35张PPT)
3.1.2 等式的性质
能否看出这些方程的解
算一算试试
(1)4x=24 (2)x+1=3
(3)5(2x+6)=3(4x-7)
(4)
我们知道,方程是含有未知数的等式,为了讨论解方程,我们先来看看等式有什么性质.
用 “=”表示相等关系的式子叫等式.
知识
准备
什么是等式?
(1)x-2=4 (2)1+2=3
(3)3a-2b (4)m+n=n+m
下面就让我们一起来讨论等式的性质吧!
a
右
左
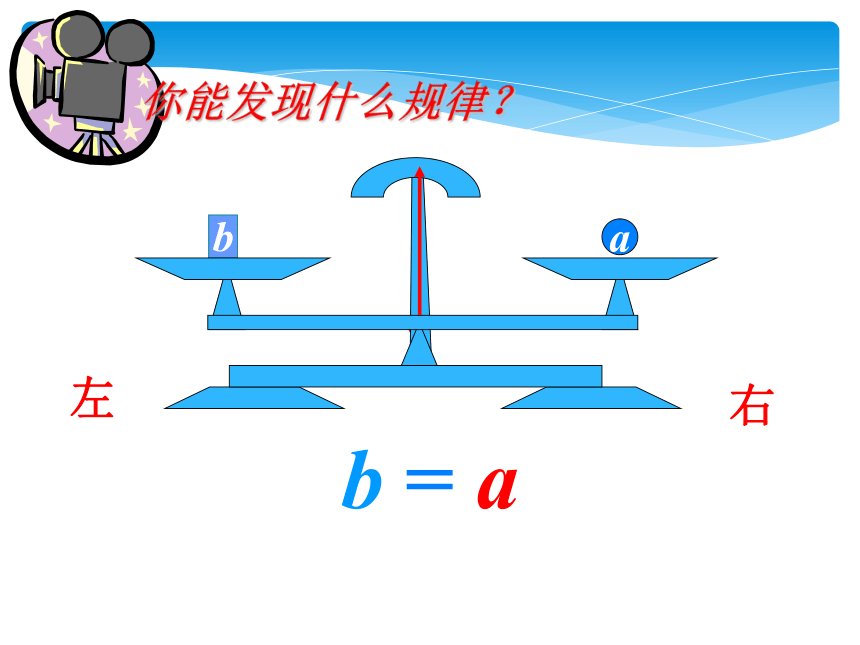
你能发现什么规律?
a
右
左
你能发现什么规律?
a
右
左
你能发现什么规律?
a
b
右
左
你能发现什么规律?
b
a
右
左
你能发现什么规律?
b
a
b = a
右
左
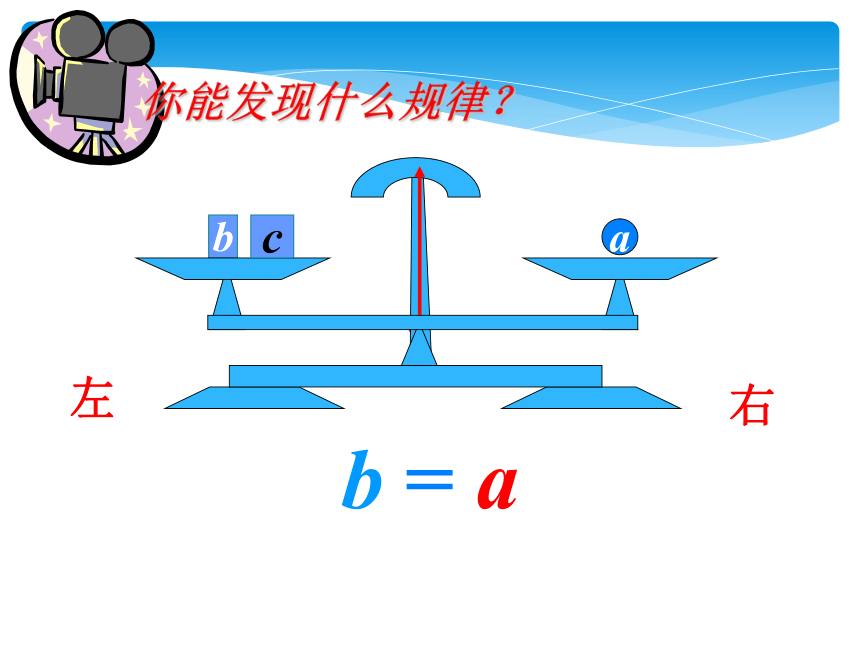
你能发现什么规律?
b
a
c
右
左
你能发现什么规律?
b = a
c
b
a
b = a
右
左
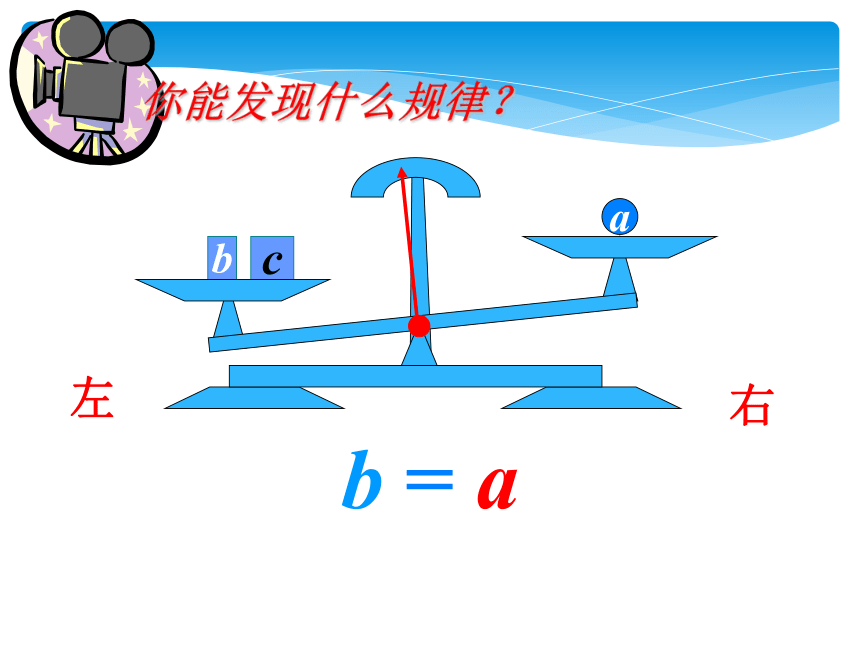
你能发现什么规律?
a
c
b
b = a
右
左
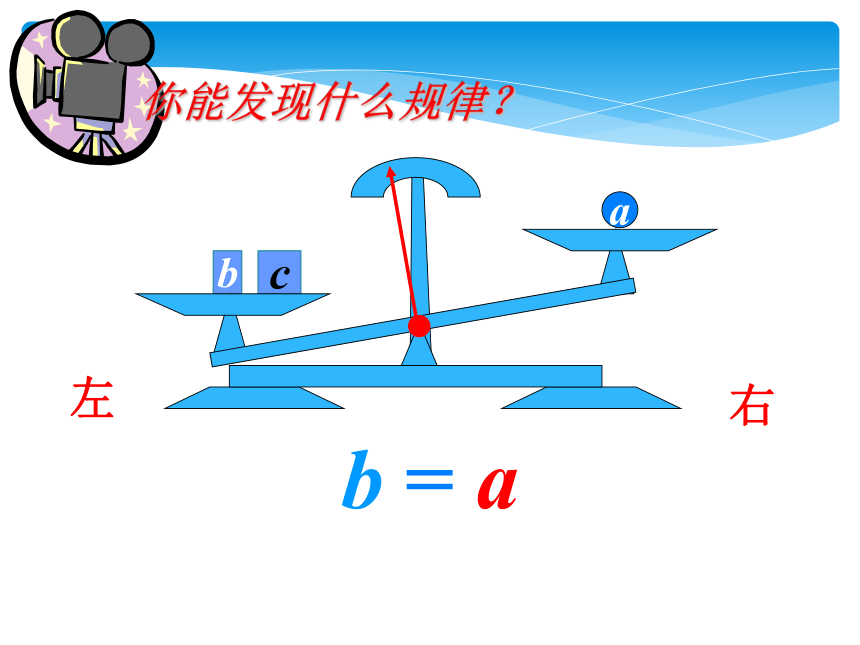
你能发现什么规律?
c
b
c
a
b = a
右
左
你能发现什么规律?
c
b
c
a
b+c a+c
=
右
左
你能发现什么规律?
b = a
c
c
右
左
你能发现什么规律?
a
b
b = a
c
右
左
你能发现什么规律?
c
右
左
你能发现什么规律?
右
左
你能发现什么规律?
b-c a-c
=
右
左
你能发现什么规律?
b = a
等式的性质1:
等式的两边都加(或都减)同一个数(或式子),结果仍相等.
性质1用式子可表示为:
如果a=b , 那么a±c=b±c
b
a
右
左
你能发现什么规律?
b = a
b
a
右
左
a
b
2b = 2a
你能发现什么规律?
b = a
b
a
右
左
b
b
a
a
3b = 3a
你能发现什么规律?
b = a
b
a
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
bc = ac
你能发现什么规律?
b = a
右
左
你能发现什么规律?
a
b
右
左
你能发现什么规律?
a
b
b
a
b = a
右
左
你能发现什么规律?
等式的性质2 :
等式的两边都乘同一个数,或除以同一个不为0的数,结果仍相等.
性质2用式子可表示为:
如果a=b, 那么 ac=bc
如果a=b ,那么
注
意
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,因为0不能作除数或分母.
(1)从 能不能得到 呢?
为什么?
练习1
(2)从 能不能得到 呢?为什么?
(3)从 能不能得到 呢?为什么?=b+2 即:a=b
=b+2 即:a=b
(4)从 能不能得到 呢?为什么?
用适当的数或式子填空,使所得的结果仍是等式,并说明根据等式的哪一条性质以及怎样变形的.
(1) 如果 2x+7=10 , 那么 2x+7-7= 10- ;
(2) 如果 5x=4x+7 , 那么 5x - = 4x+7-4x;
(3) 如果 2a=1.5 , 那么 2a×3= ;
7
4x
1.5×3
练习2
例2.用等式的性质解方程
解:两边减7,得:
解:两边同时除以-5,得:
验算:
验算:
两边同乘-3,得
解:两边加5,得:
化简得:
验算:
根据等式性质对原方程的一系列变形(两边
同加减、乘除),最终把方程化为最简的形
式:
x = a (常数)
即方程左边只一个未知数项、且未知数项
的系数是 1,右边只一个常数项.
随堂练习P83
1、利用等式的性质解下列方程
(1) x-5= 6; (2) 0.3x =45
(3) 5x+4=0; (4)
1
4
2- x= 3
3.1.2 等式的性质
能否看出这些方程的解
算一算试试
(1)4x=24 (2)x+1=3
(3)5(2x+6)=3(4x-7)
(4)
我们知道,方程是含有未知数的等式,为了讨论解方程,我们先来看看等式有什么性质.
用 “=”表示相等关系的式子叫等式.
知识
准备
什么是等式?
(1)x-2=4 (2)1+2=3
(3)3a-2b (4)m+n=n+m
下面就让我们一起来讨论等式的性质吧!
a
右
左
你能发现什么规律?
a
右
左
你能发现什么规律?
a
右
左
你能发现什么规律?
a
b
右
左
你能发现什么规律?
b
a
右
左
你能发现什么规律?
b
a
b = a
右
左
你能发现什么规律?
b
a
c
右
左
你能发现什么规律?
b = a
c
b
a
b = a
右
左
你能发现什么规律?
a
c
b
b = a
右
左
你能发现什么规律?
c
b
c
a
b = a
右
左
你能发现什么规律?
c
b
c
a
b+c a+c
=
右
左
你能发现什么规律?
b = a
c
c
右
左
你能发现什么规律?
a
b
b = a
c
右
左
你能发现什么规律?
c
右
左
你能发现什么规律?
右
左
你能发现什么规律?
b-c a-c
=
右
左
你能发现什么规律?
b = a
等式的性质1:
等式的两边都加(或都减)同一个数(或式子),结果仍相等.
性质1用式子可表示为:
如果a=b , 那么a±c=b±c
b
a
右
左
你能发现什么规律?
b = a
b
a
右
左
a
b
2b = 2a
你能发现什么规律?
b = a
b
a
右
左
b
b
a
a
3b = 3a
你能发现什么规律?
b = a
b
a
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
bc = ac
你能发现什么规律?
b = a
右
左
你能发现什么规律?
a
b
右
左
你能发现什么规律?
a
b
b
a
b = a
右
左
你能发现什么规律?
等式的性质2 :
等式的两边都乘同一个数,或除以同一个不为0的数,结果仍相等.
性质2用式子可表示为:
如果a=b, 那么 ac=bc
如果a=b ,那么
注
意
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,因为0不能作除数或分母.
(1)从 能不能得到 呢?
为什么?
练习1
(2)从 能不能得到 呢?为什么?
(3)从 能不能得到 呢?为什么?=b+2 即:a=b
=b+2 即:a=b
(4)从 能不能得到 呢?为什么?
用适当的数或式子填空,使所得的结果仍是等式,并说明根据等式的哪一条性质以及怎样变形的.
(1) 如果 2x+7=10 , 那么 2x+7-7= 10- ;
(2) 如果 5x=4x+7 , 那么 5x - = 4x+7-4x;
(3) 如果 2a=1.5 , 那么 2a×3= ;
7
4x
1.5×3
练习2
例2.用等式的性质解方程
解:两边减7,得:
解:两边同时除以-5,得:
验算:
验算:
两边同乘-3,得
解:两边加5,得:
化简得:
验算:
根据等式性质对原方程的一系列变形(两边
同加减、乘除),最终把方程化为最简的形
式:
x = a (常数)
即方程左边只一个未知数项、且未知数项
的系数是 1,右边只一个常数项.
随堂练习P83
1、利用等式的性质解下列方程
(1) x-5= 6; (2) 0.3x =45
(3) 5x+4=0; (4)
1
4
2- x= 3
