冀教版九年级数学下册29.5 第2课时与圆有关的弧长及面积的计算课件(23张ppt)
文档属性
| 名称 | 冀教版九年级数学下册29.5 第2课时与圆有关的弧长及面积的计算课件(23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
29.5 正多边形与圆
第2课时 与圆有关的弧长
及面积的计算
第二十九章 直线与圆的位置关系
课时导入
我们在小学学习了圆的面积和扇形的面积,也学习了圆的周长,那么圆上一部分的长,也就是一条弧的长怎么去求呢?现在重新学习圆的面积和扇形面积,比以前是不是有了更深的要求呢?
下面我们就来学习本节内容.
知识点
弧长公式的应用
知1-讲
感悟新知
1
思考:
我们知道,弧是圆的一部分吗,弧长就是圆周长的一部分,想一想,如何计算圆周长?圆的周长可以看作是多少度的圆心角所对的弧长?由此出发,1°的圆心角所对的弧长是多少?n°的圆心角呢?
知1-讲
感悟新知
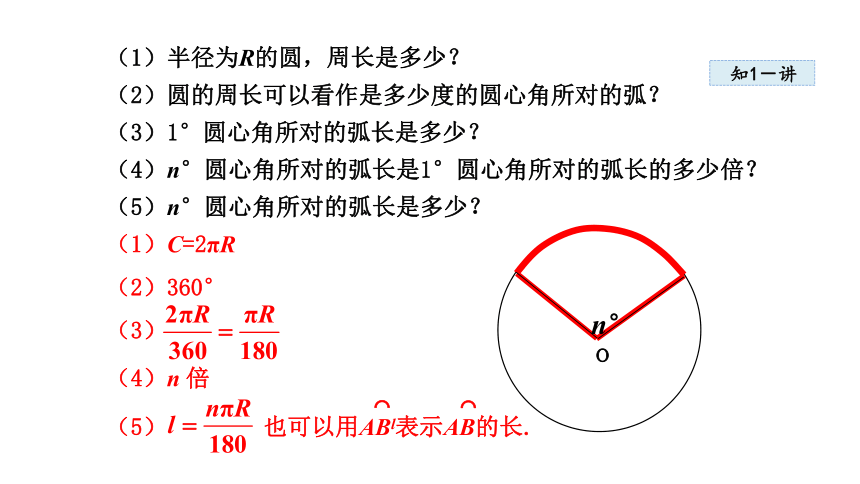
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1°圆心角所对的弧长是多少?
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n°圆心角所对的弧长是多少?
(1)C=2πR
(2)360°
(3)
(4)n 倍
(5) 也可以用ABl表示AB的长.
n°
o
⌒
⌒
感悟新知
知1-练
例 1
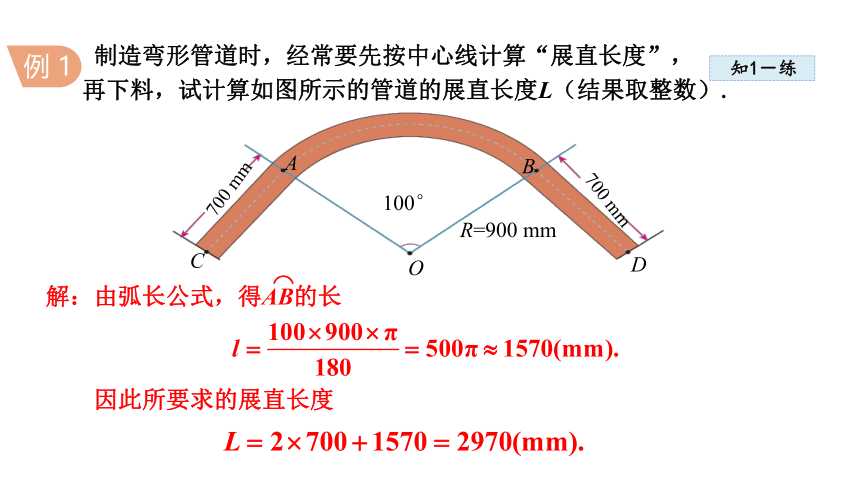
制造弯形管道时,经常要先按中心线计算“展直长度”,
再下料,试计算如图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
⌒
知1-讲
总 结
感悟新知
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
感悟新知
知1-练
例2
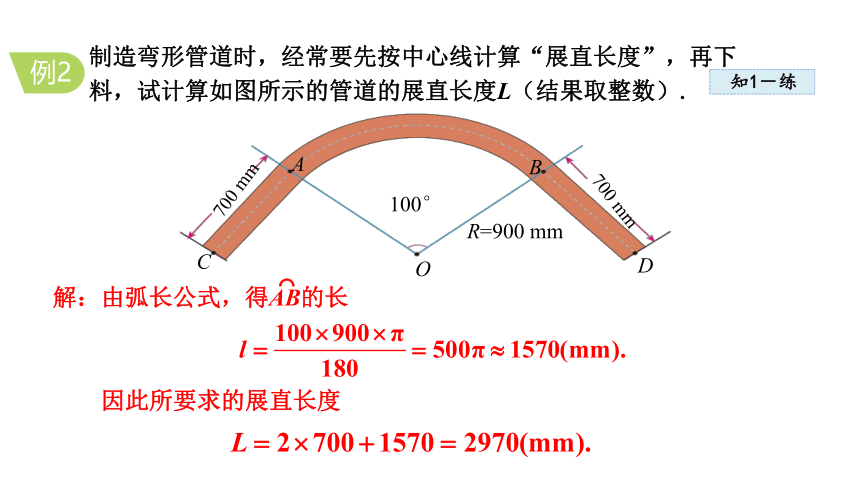
制造弯形管道时,经常要先按中心线计算“展直长度”,再下
料,试计算如图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
⌒
知1-讲
总 结
感悟新知
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
知1-讲
感悟新知
弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
易错警示:在弧长公式l= 中,n表示1°的
n倍,180表示1°的180倍,n,180不带单位.
知1-练
感悟新知
1
在在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
B
知1-练
感悟新知
1
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则BC的长等于( )
A.
B.
C.
D.
︵
A
知识点
扇形面积公式的应用
知2-讲
感悟新知
2
同学们已经学习了扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.你能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
知2-讲
感悟新知
a(地平线)
1.半径为R的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1.S=πR2
2.360°
3.
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
思考1:
知2-练
感悟新知
a(地平线)
思考1:
扇形面积的大小与哪些因素有关系?
扇形面积的大小与扇形的半径和圆心角有关.
知2-练
感悟新知
a(地平线)
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l为扇形的弧长,R为半径.
O
感悟新知
a(地平线)
例 3
如图1,水平放置的圆柱形排水管道的截
面半径是0.6 m,其中水面高 0.3 m,
求截面上有水部分的面积(结果保留小
数点后两位).
解:如图2,连接OA,OB,作弦AB的垂直平
分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
⌒
O
A
B
C
D
图1
图2
知2-练
感悟新知
a(地平线)
知2-练
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
感悟新知
知2-练
特别注意:
(1)已知S扇形,l,n,R四个量中的任意两个量,可
以求出另外两个量.
(2)在扇形面积公式S扇形= 中,n表示1°的n
倍,360表示1°的360倍,n,360不带单位.
知2-练
感悟新知
a(地平线)
如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合,若BC=4,则图中阴影部分的面积是( )
A.2+π
B.2+2π
C.4+π
D.2+4π
1
A
知2-练
感悟新知
a(地平线)
如图,AB是⊙O的直径,BT是⊙O的切线,
若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.2
B. π
C.1
D. π
2
C
课堂小结
直线与圆的位置关系
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系,
课堂小结
直线与圆的位置关系
已知AB所对的圆周角为30°,AB所在圆的半径为30 cm,求AB的长.
∵AB所对的圆周角为30°,∴AB所对的圆心角为60°,
∴AB的长l= =10π(cm).
︵
︵
︵
解:
︵
︵
︵
易错点:对弧长公式及扇形面积公式中的n的意义理解不
充分而致错.
课堂小结
直线与圆的位置关系
在公式l= ,S扇形= 中,n°是圆心角的度数,而题干给出的是圆周角的度数,不能直接代入公式计算,要求出圆心角的度数后再代入公式计算.本题易错解为
AB的长= =5π(cm).
易错总结:
︵
29.5 正多边形与圆
第2课时 与圆有关的弧长
及面积的计算
第二十九章 直线与圆的位置关系
课时导入
我们在小学学习了圆的面积和扇形的面积,也学习了圆的周长,那么圆上一部分的长,也就是一条弧的长怎么去求呢?现在重新学习圆的面积和扇形面积,比以前是不是有了更深的要求呢?
下面我们就来学习本节内容.
知识点
弧长公式的应用
知1-讲
感悟新知
1
思考:
我们知道,弧是圆的一部分吗,弧长就是圆周长的一部分,想一想,如何计算圆周长?圆的周长可以看作是多少度的圆心角所对的弧长?由此出发,1°的圆心角所对的弧长是多少?n°的圆心角呢?
知1-讲
感悟新知
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1°圆心角所对的弧长是多少?
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n°圆心角所对的弧长是多少?
(1)C=2πR
(2)360°
(3)
(4)n 倍
(5) 也可以用ABl表示AB的长.
n°
o
⌒
⌒
感悟新知
知1-练
例 1
制造弯形管道时,经常要先按中心线计算“展直长度”,
再下料,试计算如图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
⌒
知1-讲
总 结
感悟新知
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
感悟新知
知1-练
例2
制造弯形管道时,经常要先按中心线计算“展直长度”,再下
料,试计算如图所示的管道的展直长度L(结果取整数).
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
⌒
知1-讲
总 结
感悟新知
(1)应用公式时“n”和“180”不应写单位.
(2)题目若没有写明精确度,可以用含“π”的式子
表示弧长.
(3)在弧长公式中,已知l,n,R中任意两个量,
都可求出第三个量.
知1-讲
感悟新知
弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
易错警示:在弧长公式l= 中,n表示1°的
n倍,180表示1°的180倍,n,180不带单位.
知1-练
感悟新知
1
在在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
B
知1-练
感悟新知
1
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则BC的长等于( )
A.
B.
C.
D.
︵
A
知识点
扇形面积公式的应用
知2-讲
感悟新知
2
同学们已经学习了扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.你能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
知2-讲
感悟新知
a(地平线)
1.半径为R的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1.S=πR2
2.360°
3.
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
思考1:
知2-练
感悟新知
a(地平线)
思考1:
扇形面积的大小与哪些因素有关系?
扇形面积的大小与扇形的半径和圆心角有关.
知2-练
感悟新知
a(地平线)
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l为扇形的弧长,R为半径.
O
感悟新知
a(地平线)
例 3
如图1,水平放置的圆柱形排水管道的截
面半径是0.6 m,其中水面高 0.3 m,
求截面上有水部分的面积(结果保留小
数点后两位).
解:如图2,连接OA,OB,作弦AB的垂直平
分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
⌒
O
A
B
C
D
图1
图2
知2-练
感悟新知
a(地平线)
知2-练
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
感悟新知
知2-练
特别注意:
(1)已知S扇形,l,n,R四个量中的任意两个量,可
以求出另外两个量.
(2)在扇形面积公式S扇形= 中,n表示1°的n
倍,360表示1°的360倍,n,360不带单位.
知2-练
感悟新知
a(地平线)
如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合,若BC=4,则图中阴影部分的面积是( )
A.2+π
B.2+2π
C.4+π
D.2+4π
1
A
知2-练
感悟新知
a(地平线)
如图,AB是⊙O的直径,BT是⊙O的切线,
若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.2
B. π
C.1
D. π
2
C
课堂小结
直线与圆的位置关系
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系,
课堂小结
直线与圆的位置关系
已知AB所对的圆周角为30°,AB所在圆的半径为30 cm,求AB的长.
∵AB所对的圆周角为30°,∴AB所对的圆心角为60°,
∴AB的长l= =10π(cm).
︵
︵
︵
解:
︵
︵
︵
易错点:对弧长公式及扇形面积公式中的n的意义理解不
充分而致错.
课堂小结
直线与圆的位置关系
在公式l= ,S扇形= 中,n°是圆心角的度数,而题干给出的是圆周角的度数,不能直接代入公式计算,要求出圆心角的度数后再代入公式计算.本题易错解为
AB的长= =5π(cm).
易错总结:
︵
