7.3 多边形及其内角和
文档属性
| 名称 | 7.3 多边形及其内角和 |  | |
| 格式 | zip | ||
| 文件大小 | 624.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-19 22:36:27 | ||
图片预览





文档简介
(共35张PPT)
7.3 多边形及其内角和
类比三角形的定义,你能说出什么叫四边形、五边形、多边形吗?
由不在同一直线上的 线段首尾顺次相接组成的图形叫做 边形.
五
四条
四
五条
n条
n
问题1:
思考:关于多边形的定义是否正确?
一些
多
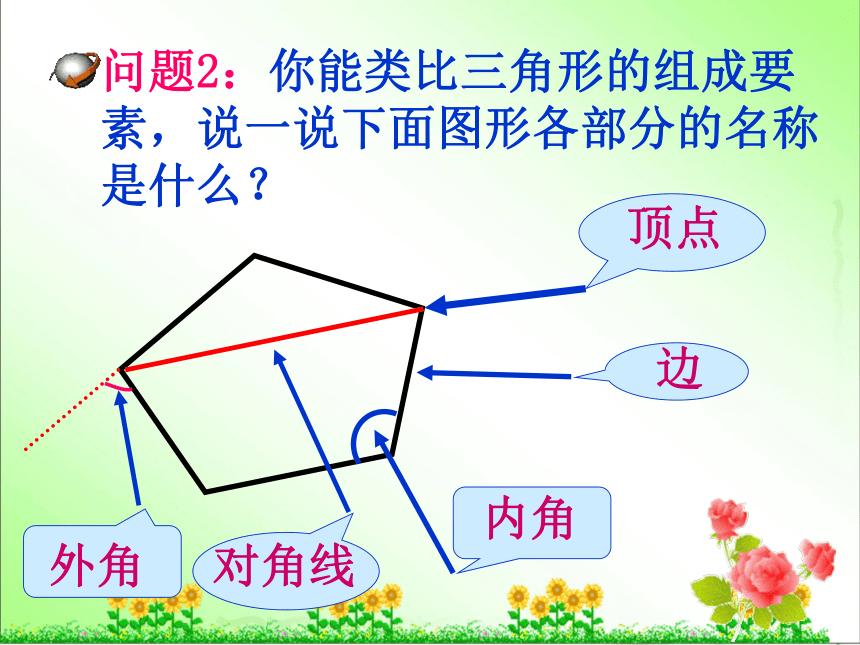
问题2:你能类比三角形的组成要素,说一说下面图形各部分的名称是什么?
边
内角
顶点
外角
对角线
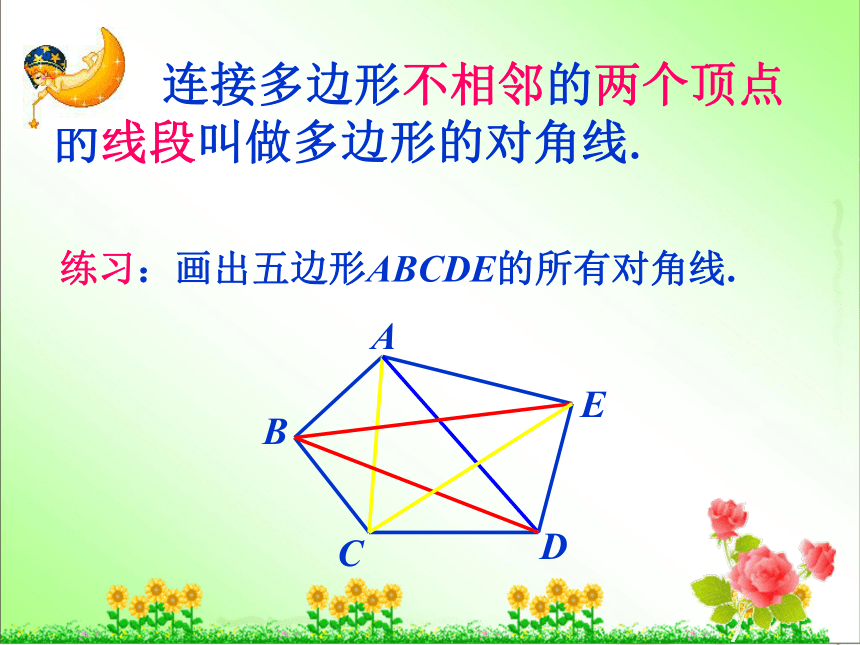
练习:画出五边形ABCDE的所有对角线.
A
B
C
E
D
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
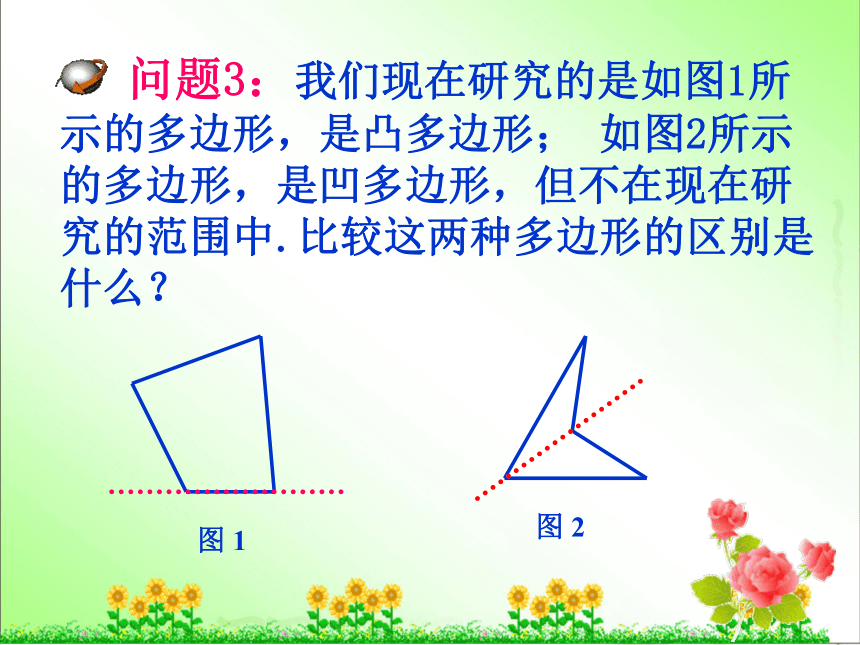
问题3:我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中.比较这两种多边形的区别是什么?
图 2
图 1
问题4:观察正三角形、正方形的特征, 猜想满足什么条件的多边形是
正多边形?
定义: 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
反例:长方形,菱形
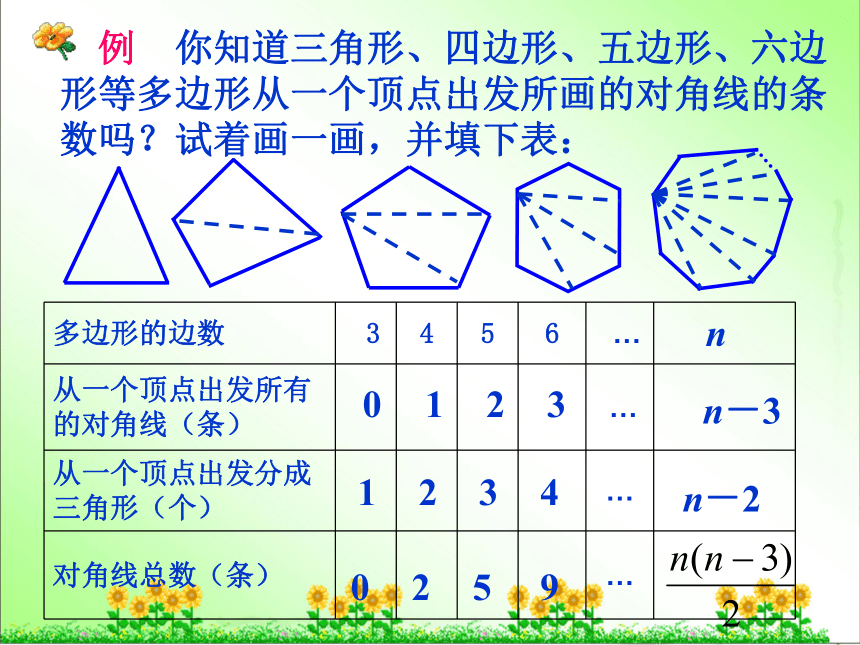
例 你知道三角形、四边形、五边形、六边形等多边形从一个顶点出发所画的对角线的条数吗?试着画一画,并填下表:
n-3
多边形的边数 3 4 5 6 … n
从一个顶点出发所有的对角线(条) …
从一个顶点出发分成三角形(个) …
对角线总数(条) …
0
1
2
3
1
2
3
4
n-2
0
2
5
9
练习测试
(2)一个多边形自一个顶点出发的对角线把它分成6个三角形,则它是__边形.
(1)如果一个多边形自一个顶点出发至多可引6条角线,则它是__边形.
九
八
三角形的内角和是180°
长方形、正方形的内角和都是360°
任意四边形的内角和是360°吗?你能画图说明吗?
(在答题纸上画出来)
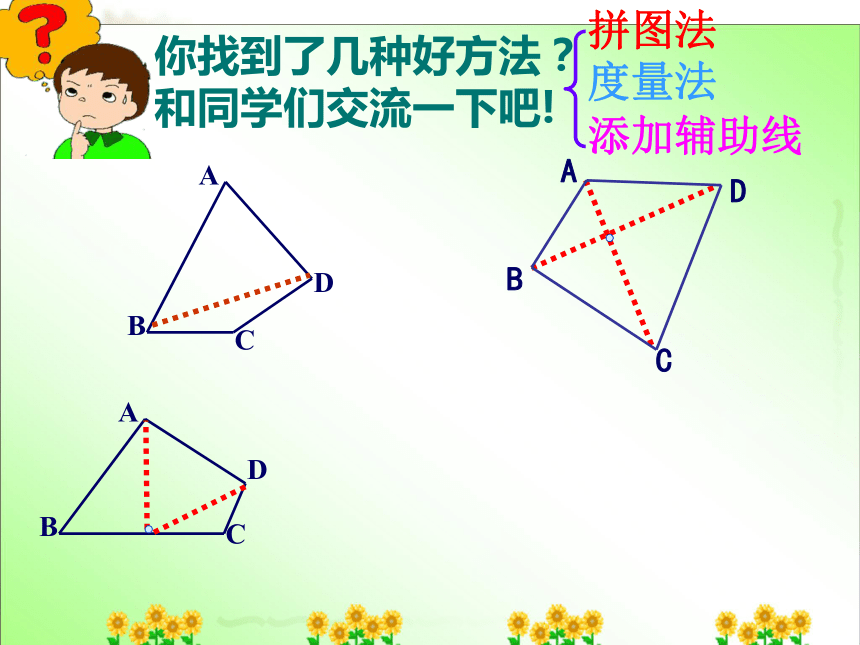
你找到了几种好方法?和同学们交流一下吧!
A
B
C
D
A
B
C
D
B
C
D
A
拼图法
度量法
添加辅助线
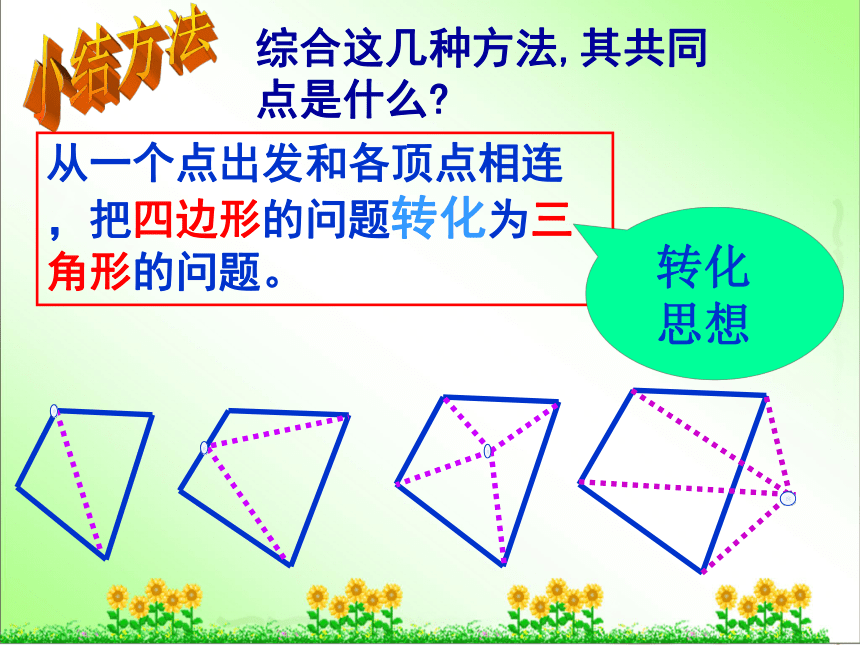
综合这几种方法,其共同点是什么
从一个点出发和各顶点相连,把四边形的问题转化为三角形的问题。
转化
思想
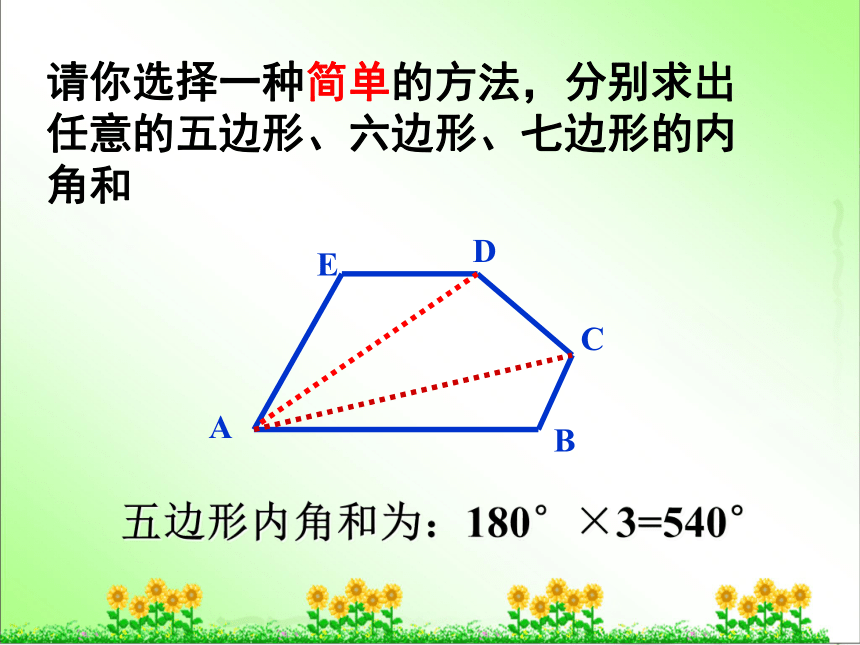
请你选择一种简单的方法,分别求出任意的五边形、六边形、七边形的内角和
A
E
D
C
B
五边形内角和为:180°×3=540°
六边形内角和为:180°×4=720°
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°
任意六边形内角和、七边形内角和
六边形内角和为:180°×4=720°
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°
任意六边形内角和、七边形内角和
多边形
的边数 图 形 多边形的
内 角 和
3
4
5
6
------ ------ ------ ------
n
n-2
1
2
3
1×180 =180
从一个顶点出发分割成的三角形个数
2×180 =360
3×180 =540
( n - 2)×180
4
4×180 =720
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(n-1)×180 °- 180 °= (n-2)×180 °
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
n边形的内角和等于
(n-2)·180°
根据以上的探讨,就得出了多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
(1)八边形的内角和等于 度
九边形的内角和等于 度
十边形的内角和等于 度
(2)一个多边形的内角和等于1800°,
这个多边形是 边形.
1080
十二
1440
1260
例3:(1)正五边形的每个内角多少度?正六边形呢?一般地,正n边形呢?
(2)一个正多边形的一个内角为150°,你知道它是几边形吗?
解: (2)设这个多边形为正n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是正十二边形。
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.试问:五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
6
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2) × 180°
=360 °
=5个平角
-5边形内角和
=5×180°
E
B
C
D
1
2
3
4
5
A
6
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360 °
练一练
2、正五边形的每一个外角等于____,每个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
X=65
X=60
X=95
X=75
P83
如果一个四边形的一组对角互补,
那么另一组对角有什么关系
如图,已知四边形ABCD中∠A+∠C=180°,
求∠B + ∠D
A
D
B
C
解:因为
∠A+ ∠ B+∠ C+ ∠D=360°
所以
∠ B+∠D =360°-(∠A+ ∠ C)
=360°- 180°
=180°
3、已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=___
A
B
C
D
E
1
2
220°
如图:
求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F=
E
A
B
C
D
F
1
2
如图:
求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F+ ∠G=
F
A
B
C
D
E
G
解:假设这个多边形的边数是n,那个内角的度数为x
则有:(n-2)x180=2750+x
因为n是正整数,所以2750+x也是180的倍数
因为x<180
所以x=130
所以(n-2).180=2880
所以n=18
1、已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
拓展练习
D
C
B
E
A
F
∠F=360
解:因为五边形ABCDE是正五边形
所以∠BAE=∠DAE
=108°
所以∠FAE=72°,∠FEA=72°
2、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
拓展练习
3、在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
拓展练习
一、n边形的内角和公式
(n-2)·180°
二、几种数学思想:
转化思想、方程思想
7.3 多边形及其内角和
类比三角形的定义,你能说出什么叫四边形、五边形、多边形吗?
由不在同一直线上的 线段首尾顺次相接组成的图形叫做 边形.
五
四条
四
五条
n条
n
问题1:
思考:关于多边形的定义是否正确?
一些
多
问题2:你能类比三角形的组成要素,说一说下面图形各部分的名称是什么?
边
内角
顶点
外角
对角线
练习:画出五边形ABCDE的所有对角线.
A
B
C
E
D
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
问题3:我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中.比较这两种多边形的区别是什么?
图 2
图 1
问题4:观察正三角形、正方形的特征, 猜想满足什么条件的多边形是
正多边形?
定义: 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
反例:长方形,菱形
例 你知道三角形、四边形、五边形、六边形等多边形从一个顶点出发所画的对角线的条数吗?试着画一画,并填下表:
n-3
多边形的边数 3 4 5 6 … n
从一个顶点出发所有的对角线(条) …
从一个顶点出发分成三角形(个) …
对角线总数(条) …
0
1
2
3
1
2
3
4
n-2
0
2
5
9
练习测试
(2)一个多边形自一个顶点出发的对角线把它分成6个三角形,则它是__边形.
(1)如果一个多边形自一个顶点出发至多可引6条角线,则它是__边形.
九
八
三角形的内角和是180°
长方形、正方形的内角和都是360°
任意四边形的内角和是360°吗?你能画图说明吗?
(在答题纸上画出来)
你找到了几种好方法?和同学们交流一下吧!
A
B
C
D
A
B
C
D
B
C
D
A
拼图法
度量法
添加辅助线
综合这几种方法,其共同点是什么
从一个点出发和各顶点相连,把四边形的问题转化为三角形的问题。
转化
思想
请你选择一种简单的方法,分别求出任意的五边形、六边形、七边形的内角和
A
E
D
C
B
五边形内角和为:180°×3=540°
六边形内角和为:180°×4=720°
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°
任意六边形内角和、七边形内角和
六边形内角和为:180°×4=720°
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°
任意六边形内角和、七边形内角和
多边形
的边数 图 形 多边形的
内 角 和
3
4
5
6
------ ------ ------ ------
n
n-2
1
2
3
1×180 =180
从一个顶点出发分割成的三角形个数
2×180 =360
3×180 =540
( n - 2)×180
4
4×180 =720
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(n-1)×180 °- 180 °= (n-2)×180 °
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
n边形的内角和等于
(n-2)·180°
根据以上的探讨,就得出了多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
(1)八边形的内角和等于 度
九边形的内角和等于 度
十边形的内角和等于 度
(2)一个多边形的内角和等于1800°,
这个多边形是 边形.
1080
十二
1440
1260
例3:(1)正五边形的每个内角多少度?正六边形呢?一般地,正n边形呢?
(2)一个正多边形的一个内角为150°,你知道它是几边形吗?
解: (2)设这个多边形为正n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是正十二边形。
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.试问:五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
6
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2) × 180°
=360 °
=5个平角
-5边形内角和
=5×180°
E
B
C
D
1
2
3
4
5
A
6
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360 °
练一练
2、正五边形的每一个外角等于____,每个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
X=65
X=60
X=95
X=75
P83
如果一个四边形的一组对角互补,
那么另一组对角有什么关系
如图,已知四边形ABCD中∠A+∠C=180°,
求∠B + ∠D
A
D
B
C
解:因为
∠A+ ∠ B+∠ C+ ∠D=360°
所以
∠ B+∠D =360°-(∠A+ ∠ C)
=360°- 180°
=180°
3、已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=___
A
B
C
D
E
1
2
220°
如图:
求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F=
E
A
B
C
D
F
1
2
如图:
求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F+ ∠G=
F
A
B
C
D
E
G
解:假设这个多边形的边数是n,那个内角的度数为x
则有:(n-2)x180=2750+x
因为n是正整数,所以2750+x也是180的倍数
因为x<180
所以x=130
所以(n-2).180=2880
所以n=18
1、已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
拓展练习
D
C
B
E
A
F
∠F=360
解:因为五边形ABCDE是正五边形
所以∠BAE=∠DAE
=108°
所以∠FAE=72°,∠FEA=72°
2、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
拓展练习
3、在多边形的所有外角中最多有几个钝角?在多边形的所有内角中最多有几个锐角?
拓展练习
一、n边形的内角和公式
(n-2)·180°
二、几种数学思想:
转化思想、方程思想
