2.1.1倾斜角和斜率 同步学案(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 2.1.1倾斜角和斜率 同步学案(知识梳理+例题+变式+练习)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.1.1倾斜角和斜率
要点一 直线的倾斜角
1.倾斜角的定义:当直线l与x轴相交时,取x轴作为基准,x轴_正方向_与直线l__向上__方向之间所成的角叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠APx,直线l′的倾斜角是∠BPx.
2.倾斜角的范围:直线的倾斜角α的取值范围是_ _,并规定与x轴平行或重合的直线的倾斜角为_ _.
【知识技巧】
由倾斜角的定义可以知道,任何一条直线都有倾斜角;不同的直线其倾斜角有可能相同,如平行的直线其倾斜角是相同的.
要点二 直线的斜率
1.斜率的定义:一条直线的倾斜角α(α≠90°)的_正切__值叫做这条直线的斜率.常用小写字母k表示,即k=__ ___.
2.斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k=__ __,当x1=x2时,直线P1P2没有斜率.
3.斜率的作用:用实数反映了平面直角坐标系内的直线的_直线的倾斜程度_.
【方法技巧】
斜率与倾斜角的对应关系.
图示
倾斜角(范围) α=0 ° 0 °<α<90 ° α=90 ° 90 °<α<180 °
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)若α是直线l的倾斜角,则0°≤α<180°.( )
(2)若k是直线的斜率,则k∈R.( )
(3)任一条直线都有倾斜角,但不一定有斜率.( )
(4)任一条直线都有斜率,但不一定有倾斜角.( )
【答案】(1)√(2)√(3)√(4)×
2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( )
A.0° B.45°C.60° D.90°
【答案】A
【解析】∵k==0,∴θ=0°.
3.已知直线l的倾斜角为30°,则直线l的斜率为( )
A. B. C.1 D.
【答案】A
【解析】由题意可知,k=tan 30°=.故选A.
4.已知直线AB与直线AC有相同的斜率,且A(1,0),B(2,a),C(a,1),则实数a的值是________.
【答案】
【解析】依题意:kAB=kAC,即=,解得a=.
题型一 求直线的倾斜角
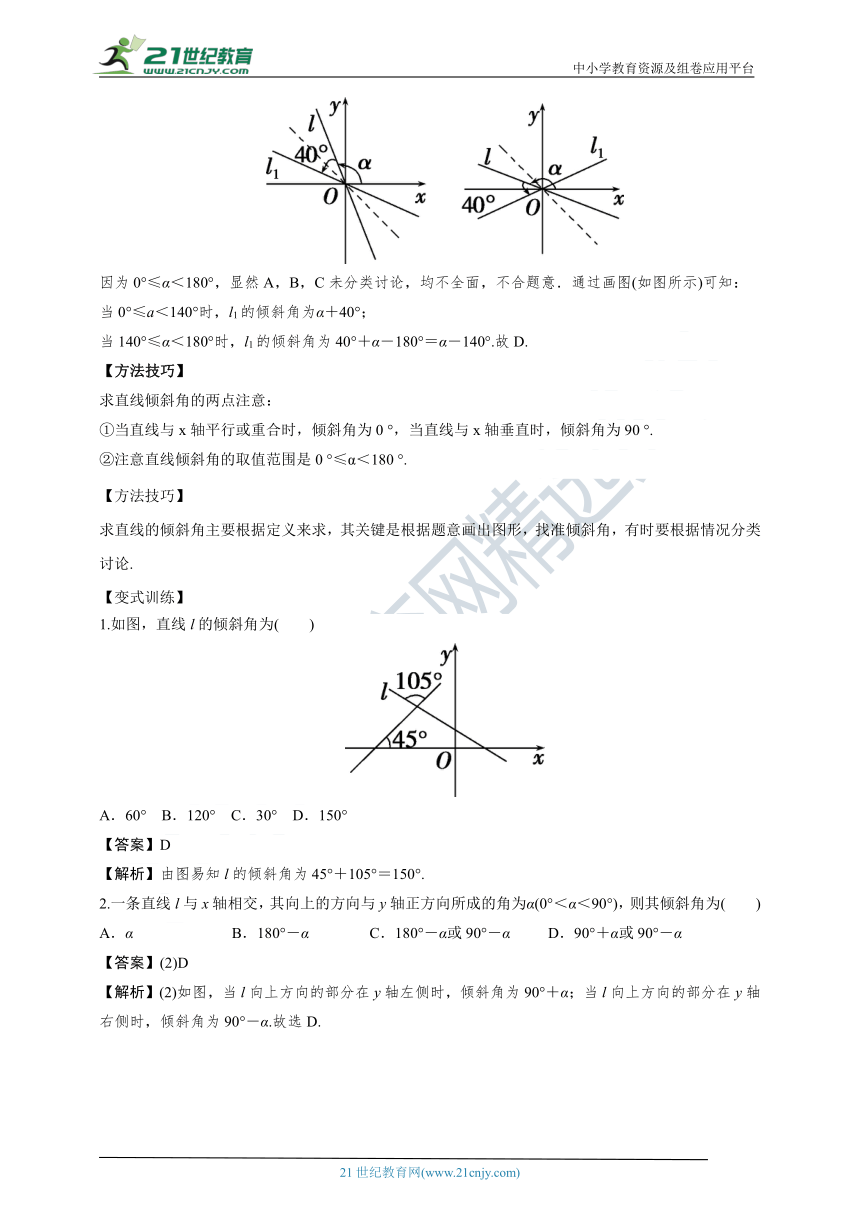
【例1】设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转40°,得直线l1,则直线l1的倾斜角为( )
A.α+40°
B.α-140°
C.140°-α
D.当0°≤α<140°时为α+40°,当140°≤α<180°时为α-140°
【答案】D
【解析】根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:
当0°≤a<140°时,l1的倾斜角为α+40°;
当140°≤α<180°时,l1的倾斜角为40°+α-180°=α-140°.故D.
【方法技巧】
求直线倾斜角的两点注意:
①当直线与x轴平行或重合时,倾斜角为0 °,当直线与x轴垂直时,倾斜角为90 °.
②注意直线倾斜角的取值范围是0 °≤α<180 °.
【方法技巧】
求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
【变式训练】
1.如图,直线l的倾斜角为( )
A.60° B.120° C.30° D.150°
【答案】D
【解析】由图易知l的倾斜角为45°+105°=150°.
2.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α C.180°-α或90°-α D.90°+α或90°-α
【答案】(2)D
【解析】(2)如图,当l向上方向的部分在y轴左侧时,倾斜角为90°+α;当l向上方向的部分在y轴右侧时,倾斜角为90°-α.故选D.
题型二 求直线的斜率
【例2】
(1)如图,直线l1的倾斜角α1=30°,直线l1⊥l2,求l1、l2的斜率;
(2)求经过两点A(a,2),B(3,6)的直线的斜率.
【解析】(1)l1的斜率k1=tan α1=tan 30°=.
∵l2的倾斜角α2=90°+30°=120°,∴l2的斜率k2=tan 120°=tan(180°-60°)=-tan 60°=-.
(2)当a=3时,斜率不存在;
当a≠3时,直线的斜率k=.
【方法技巧】
1.由倾斜角(或范围)求斜率(或范围)利用定义式k=tan α(α≠90°)解决.
2.由两点坐标求斜率运用两点斜率公式k=(x1≠x2)求解.
3.涉及直线与线段有交点问题常数形结合利用公式求解.
【变式训练】
(1)已知过两点A(4,y),B(2,-3)的直线的倾斜角为135°,则y=________;
(2)过点P(-2,m),Q(m,4)的直线的斜率为1,则m的值为________.
【答案】(1)-5 (2)1
【解析】(1)直线AB的斜率k=tan 135°=-1,又k=,由=-1,得y=-5.
(2)由斜率公式k==1,得m=1
题型三 直线斜率的应用
【例3】已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
【分析】结合图形考虑,l的倾斜角应介于直线PB与直线PA的倾斜角之间,要特别注意,当l的倾斜角小于90 °时,有k≥kPB;当l的倾斜角大于90 °时,则有k≤kPA.
【解析】如图,由题意可知kPA==-1,kPB==1,
(1)要使l与线段AB有公共点,则直线l的斜率k的取值范围是(-∞,-1]∪[1,+∞).
(2)由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,∴α的取值范围是45°≤α≤135°.
【方法技巧】
①直线都有倾斜角,但并不是所有的直线都有斜率.当倾斜角是90 °时.直线的斜率不存在,此时,直线垂直于x轴(平行于y轴或与y轴重合).
②直线的斜率也反映了直线相对于x轴的正方向的倾斜程度.当0 °≤α<90 °时,斜率越大,直线的倾斜程度越大;当90 °<α<180 °时,斜率越大,直线的倾斜程度也越大.
【变式训练】
1.已知A(3,3),B(-4,2),C(0,-2),
(1)求直线AB和AC的斜率.
(2)若点D在线段BC(包括端点)上移动时,求直线AD的斜率的变化范围.
【解析】(1)由斜率公式可得直线AB的斜率kAB==.直线AC的斜率kAC==.故直线AB的斜率为,直线AC的斜率为.
(2)如图所示,当D由B运动到C时,直线AD的斜率由kAB增大到kAC,所以直线AD的斜率的变化范围是[,].
1.过点A(-,)与点B(-,)的直线的倾斜角为( )
A.45° B.135°
C.45°或135° D.60°
【答案】A
【解析】因为斜率k==1,所以倾斜角为45°.
2.若图中直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1B.k3C.k3D.k1【答案】D
【解析】由题图可知,k1<0,k2>0,k3>0,且l2比l3的倾斜角大,∴k13.若点A(-1,-2),B(4,8),已知AB的方向向量为(1,k),则实数k的值为( )
A. B.- C.2 D.-2
【答案】C
【解析】AB的方向向量坐标为(4+1,8+2),即(5,10).又(1,k)也是AB的方向向量,∴k==2.]
4.设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
【答案】D
【解析】根据题意,画出图形,如图所示.
A,B,C未分类讨论,均不全面,不合题意.通过图形可知:
当0°≤α<135°时,l1的倾斜角为α+45°;
当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.]
5.如果直线l过点(1,2),且不通过第四象限,那么l的斜率的取值范围是( )
A.[0,1] B.[0,2]
C. D.(0,3]
【答案】B
【解析】如图,经过(1,2)和(0,0)的斜率k=2,若l不通过第四象限,则0≤k≤2.故选B.]
6.设P为x轴上的一点,A(-3,8),B(2,14),若直线PA的斜率kPA是直线PB的斜率kPB的2倍,则点P的坐标为________.
【答案】(-5,0)
【解析】[设P(x,0),由条件kPA=2kPB,则=2×,解得x=-5,故P(-5,0).]
7.已知点A(1,2),若在坐标轴上有一点P,使直线PA的倾斜角为135°,则点P的坐标为________.
【答案】(3,0)或(0,3)
【解析】 [由题意知kPA=-1,若P点在x轴上,则设P(m,0),则=-1,解得m=3;若P点在y轴上,则设P(0,n),则=-1,解得n=3,故P点的坐标为(3,0)或(0,3).]
8.若经过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为锐角,则实数a的取值范围是________.
【答案】(-∞,-2)∪(1,+∞)
【解析】 [由k==>0得a>1或a<-2.]
9.求证:A(1,-1),B(-2,-7),C(0,-3)三点共线.
【解析】∵A(1,-1),B(-2,-7),C(0,-3),
∴kAB==2,kAC==2.∴kAB=kAC.
∵直线AB与直线AC的倾斜角相同且过同一点A,
∴直线AB与直线AC为同一直线.
故A,B,C三点共线.
10.已知直线l的倾斜角α的范围是45°≤α≤135°,求直线l的斜率k的范围.
【解析】分类讨论:当α=90°时,l的斜率不存在;
当45°≤α<90°时,l的斜率k=tan α∈[1,+∞);
当90°<α≤135°时,l的斜率k=tan α∈(-∞,-1].
∴l的斜率不存在或斜率k∈(-∞,-1]∪[1,+∞).
11.(多选题)若两直线l1,l2的倾斜角分别为α1,α2,则下列四个命题中错误的是( )
A.若α1<α2,则两直线的斜率:k1<k2
B.若α1=α2,则两直线的斜率:k1=k2
C.若两直线的斜率:k1<k2,则α1<α2
D.若两直线的斜率:k1=k2,则α1=α2
【答案】ABC
【解析】当α1=30°,α2=120°,满足α1<α2,但是两直线的斜率k1>k2,选项A说法错误;当α1=α2=90°时,直线的斜率不存在,无法满足k1=k2,选项B说法错误;若直线的斜率k1=-1,k2=1,满足k1<k2,但是α1=135°,α2=45°,不满足α1<α2,选项C说法错误;若k1=k2说明斜率一定存在,则必有α1=α2,选项D正确.]
12.将直线l向右平移4个单位,再向下平移5个单位后仍回到原来的位置,则此直线的斜率为( )
A. B. C.- D.-
【答案】C
【解析】设点P(a,b)是直线l上的任意一点,当直线l按题中要求平移后,点P也做同样的平移,平移后的坐标为(a+4,b-5),由题意知,这两点都在直线l上,∴直线l的斜率为k==-.]
13.(一题两空)直线l经过点(-1,0),倾斜角为150°,若将直线l绕点(-1,0)逆时针旋转60°后,得到直线l′,则直线l′的倾斜角为________,斜率为________.
【答案】30°
【解析】如图所示.
∵直线l的倾斜角为150°,∴绕点(-1,0)逆时针旋转60°后,所得直线l′的倾斜角α=(150°+60°)-180°=30°, 斜率k=tan α=tan 30°=.
14.已知两点A(-3,4),B(3,2),过点P(2,-1)的直线l与线段AB有公共点,则l的斜率的取值范围为________.
【答案】(-∞,-1]∪[3,+∞)
【解析】如图,要使l与线段AB有公共点,则直线l的倾斜角介于直线PB与直线PA的倾斜角之间.当直线l的倾斜角为钝角时,∵直线PA的斜率为=-1,∴k∈(-∞,-1],
当l的倾斜角为锐角时,又直线PB的斜率为=3,∴k∈[3,+∞).故k∈(-∞,-1]∪[3,+∞).
15.已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).
(1)求直线AB,BC,AC的斜率和倾斜角;
(2)若D为△ABC的边AB上一动点,求直线CD斜率k的取值范围.
【解析】(1)由斜率公式得kAB==0,
kBC==,kAC==.
倾斜角的取值在区间[0°,180°)范围内,∵tan 0°=0,
∴直线AB的倾斜角为0°.∵tan 60°=,∴直线BC的倾斜角为60°.
∵tan 30°=,∴直线AC的倾斜角为30°.
(2)如图,当斜率k变化时,直线CD绕点C旋转,当直线CD由CA逆时针转到CB时,直线CD与AB恒有交点,即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.1.1倾斜角和斜率
要点一 直线的倾斜角
1.倾斜角的定义:当直线l与x轴相交时,取x轴作为基准,x轴_正方向_与直线l__向上__方向之间所成的角叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠APx,直线l′的倾斜角是∠BPx.
2.倾斜角的范围:直线的倾斜角α的取值范围是_ _,并规定与x轴平行或重合的直线的倾斜角为_ _.
【知识技巧】
由倾斜角的定义可以知道,任何一条直线都有倾斜角;不同的直线其倾斜角有可能相同,如平行的直线其倾斜角是相同的.
要点二 直线的斜率
1.斜率的定义:一条直线的倾斜角α(α≠90°)的_正切__值叫做这条直线的斜率.常用小写字母k表示,即k=__ ___.
2.斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k=__ __,当x1=x2时,直线P1P2没有斜率.
3.斜率的作用:用实数反映了平面直角坐标系内的直线的_直线的倾斜程度_.
【方法技巧】
斜率与倾斜角的对应关系.
图示
倾斜角(范围) α=0 ° 0 °<α<90 ° α=90 ° 90 °<α<180 °
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)若α是直线l的倾斜角,则0°≤α<180°.( )
(2)若k是直线的斜率,则k∈R.( )
(3)任一条直线都有倾斜角,但不一定有斜率.( )
(4)任一条直线都有斜率,但不一定有倾斜角.( )
【答案】(1)√(2)√(3)√(4)×
2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( )
A.0° B.45°C.60° D.90°
【答案】A
【解析】∵k==0,∴θ=0°.
3.已知直线l的倾斜角为30°,则直线l的斜率为( )
A. B. C.1 D.
【答案】A
【解析】由题意可知,k=tan 30°=.故选A.
4.已知直线AB与直线AC有相同的斜率,且A(1,0),B(2,a),C(a,1),则实数a的值是________.
【答案】
【解析】依题意:kAB=kAC,即=,解得a=.
题型一 求直线的倾斜角
【例1】设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转40°,得直线l1,则直线l1的倾斜角为( )
A.α+40°
B.α-140°
C.140°-α
D.当0°≤α<140°时为α+40°,当140°≤α<180°时为α-140°
【答案】D
【解析】根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:
当0°≤a<140°时,l1的倾斜角为α+40°;
当140°≤α<180°时,l1的倾斜角为40°+α-180°=α-140°.故D.
【方法技巧】
求直线倾斜角的两点注意:
①当直线与x轴平行或重合时,倾斜角为0 °,当直线与x轴垂直时,倾斜角为90 °.
②注意直线倾斜角的取值范围是0 °≤α<180 °.
【方法技巧】
求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
【变式训练】
1.如图,直线l的倾斜角为( )
A.60° B.120° C.30° D.150°
【答案】D
【解析】由图易知l的倾斜角为45°+105°=150°.
2.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α C.180°-α或90°-α D.90°+α或90°-α
【答案】(2)D
【解析】(2)如图,当l向上方向的部分在y轴左侧时,倾斜角为90°+α;当l向上方向的部分在y轴右侧时,倾斜角为90°-α.故选D.
题型二 求直线的斜率
【例2】
(1)如图,直线l1的倾斜角α1=30°,直线l1⊥l2,求l1、l2的斜率;
(2)求经过两点A(a,2),B(3,6)的直线的斜率.
【解析】(1)l1的斜率k1=tan α1=tan 30°=.
∵l2的倾斜角α2=90°+30°=120°,∴l2的斜率k2=tan 120°=tan(180°-60°)=-tan 60°=-.
(2)当a=3时,斜率不存在;
当a≠3时,直线的斜率k=.
【方法技巧】
1.由倾斜角(或范围)求斜率(或范围)利用定义式k=tan α(α≠90°)解决.
2.由两点坐标求斜率运用两点斜率公式k=(x1≠x2)求解.
3.涉及直线与线段有交点问题常数形结合利用公式求解.
【变式训练】
(1)已知过两点A(4,y),B(2,-3)的直线的倾斜角为135°,则y=________;
(2)过点P(-2,m),Q(m,4)的直线的斜率为1,则m的值为________.
【答案】(1)-5 (2)1
【解析】(1)直线AB的斜率k=tan 135°=-1,又k=,由=-1,得y=-5.
(2)由斜率公式k==1,得m=1
题型三 直线斜率的应用
【例3】已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
【分析】结合图形考虑,l的倾斜角应介于直线PB与直线PA的倾斜角之间,要特别注意,当l的倾斜角小于90 °时,有k≥kPB;当l的倾斜角大于90 °时,则有k≤kPA.
【解析】如图,由题意可知kPA==-1,kPB==1,
(1)要使l与线段AB有公共点,则直线l的斜率k的取值范围是(-∞,-1]∪[1,+∞).
(2)由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,∴α的取值范围是45°≤α≤135°.
【方法技巧】
①直线都有倾斜角,但并不是所有的直线都有斜率.当倾斜角是90 °时.直线的斜率不存在,此时,直线垂直于x轴(平行于y轴或与y轴重合).
②直线的斜率也反映了直线相对于x轴的正方向的倾斜程度.当0 °≤α<90 °时,斜率越大,直线的倾斜程度越大;当90 °<α<180 °时,斜率越大,直线的倾斜程度也越大.
【变式训练】
1.已知A(3,3),B(-4,2),C(0,-2),
(1)求直线AB和AC的斜率.
(2)若点D在线段BC(包括端点)上移动时,求直线AD的斜率的变化范围.
【解析】(1)由斜率公式可得直线AB的斜率kAB==.直线AC的斜率kAC==.故直线AB的斜率为,直线AC的斜率为.
(2)如图所示,当D由B运动到C时,直线AD的斜率由kAB增大到kAC,所以直线AD的斜率的变化范围是[,].
1.过点A(-,)与点B(-,)的直线的倾斜角为( )
A.45° B.135°
C.45°或135° D.60°
【答案】A
【解析】因为斜率k==1,所以倾斜角为45°.
2.若图中直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1
【解析】由题图可知,k1<0,k2>0,k3>0,且l2比l3的倾斜角大,∴k1
A. B.- C.2 D.-2
【答案】C
【解析】AB的方向向量坐标为(4+1,8+2),即(5,10).又(1,k)也是AB的方向向量,∴k==2.]
4.设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
【答案】D
【解析】根据题意,画出图形,如图所示.
A,B,C未分类讨论,均不全面,不合题意.通过图形可知:
当0°≤α<135°时,l1的倾斜角为α+45°;
当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.]
5.如果直线l过点(1,2),且不通过第四象限,那么l的斜率的取值范围是( )
A.[0,1] B.[0,2]
C. D.(0,3]
【答案】B
【解析】如图,经过(1,2)和(0,0)的斜率k=2,若l不通过第四象限,则0≤k≤2.故选B.]
6.设P为x轴上的一点,A(-3,8),B(2,14),若直线PA的斜率kPA是直线PB的斜率kPB的2倍,则点P的坐标为________.
【答案】(-5,0)
【解析】[设P(x,0),由条件kPA=2kPB,则=2×,解得x=-5,故P(-5,0).]
7.已知点A(1,2),若在坐标轴上有一点P,使直线PA的倾斜角为135°,则点P的坐标为________.
【答案】(3,0)或(0,3)
【解析】 [由题意知kPA=-1,若P点在x轴上,则设P(m,0),则=-1,解得m=3;若P点在y轴上,则设P(0,n),则=-1,解得n=3,故P点的坐标为(3,0)或(0,3).]
8.若经过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为锐角,则实数a的取值范围是________.
【答案】(-∞,-2)∪(1,+∞)
【解析】 [由k==>0得a>1或a<-2.]
9.求证:A(1,-1),B(-2,-7),C(0,-3)三点共线.
【解析】∵A(1,-1),B(-2,-7),C(0,-3),
∴kAB==2,kAC==2.∴kAB=kAC.
∵直线AB与直线AC的倾斜角相同且过同一点A,
∴直线AB与直线AC为同一直线.
故A,B,C三点共线.
10.已知直线l的倾斜角α的范围是45°≤α≤135°,求直线l的斜率k的范围.
【解析】分类讨论:当α=90°时,l的斜率不存在;
当45°≤α<90°时,l的斜率k=tan α∈[1,+∞);
当90°<α≤135°时,l的斜率k=tan α∈(-∞,-1].
∴l的斜率不存在或斜率k∈(-∞,-1]∪[1,+∞).
11.(多选题)若两直线l1,l2的倾斜角分别为α1,α2,则下列四个命题中错误的是( )
A.若α1<α2,则两直线的斜率:k1<k2
B.若α1=α2,则两直线的斜率:k1=k2
C.若两直线的斜率:k1<k2,则α1<α2
D.若两直线的斜率:k1=k2,则α1=α2
【答案】ABC
【解析】当α1=30°,α2=120°,满足α1<α2,但是两直线的斜率k1>k2,选项A说法错误;当α1=α2=90°时,直线的斜率不存在,无法满足k1=k2,选项B说法错误;若直线的斜率k1=-1,k2=1,满足k1<k2,但是α1=135°,α2=45°,不满足α1<α2,选项C说法错误;若k1=k2说明斜率一定存在,则必有α1=α2,选项D正确.]
12.将直线l向右平移4个单位,再向下平移5个单位后仍回到原来的位置,则此直线的斜率为( )
A. B. C.- D.-
【答案】C
【解析】设点P(a,b)是直线l上的任意一点,当直线l按题中要求平移后,点P也做同样的平移,平移后的坐标为(a+4,b-5),由题意知,这两点都在直线l上,∴直线l的斜率为k==-.]
13.(一题两空)直线l经过点(-1,0),倾斜角为150°,若将直线l绕点(-1,0)逆时针旋转60°后,得到直线l′,则直线l′的倾斜角为________,斜率为________.
【答案】30°
【解析】如图所示.
∵直线l的倾斜角为150°,∴绕点(-1,0)逆时针旋转60°后,所得直线l′的倾斜角α=(150°+60°)-180°=30°, 斜率k=tan α=tan 30°=.
14.已知两点A(-3,4),B(3,2),过点P(2,-1)的直线l与线段AB有公共点,则l的斜率的取值范围为________.
【答案】(-∞,-1]∪[3,+∞)
【解析】如图,要使l与线段AB有公共点,则直线l的倾斜角介于直线PB与直线PA的倾斜角之间.当直线l的倾斜角为钝角时,∵直线PA的斜率为=-1,∴k∈(-∞,-1],
当l的倾斜角为锐角时,又直线PB的斜率为=3,∴k∈[3,+∞).故k∈(-∞,-1]∪[3,+∞).
15.已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).
(1)求直线AB,BC,AC的斜率和倾斜角;
(2)若D为△ABC的边AB上一动点,求直线CD斜率k的取值范围.
【解析】(1)由斜率公式得kAB==0,
kBC==,kAC==.
倾斜角的取值在区间[0°,180°)范围内,∵tan 0°=0,
∴直线AB的倾斜角为0°.∵tan 60°=,∴直线BC的倾斜角为60°.
∵tan 30°=,∴直线AC的倾斜角为30°.
(2)如图,当斜率k变化时,直线CD绕点C旋转,当直线CD由CA逆时针转到CB时,直线CD与AB恒有交点,即D在线段AB上,此时k由kCA增大到kCB,所以k的取值范围为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
