冀教版九年级数学下册30.1 二次函数 课件(共30张PPT)
文档属性
| 名称 | 冀教版九年级数学下册30.1 二次函数 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第三十章 二次函数
第1节 二次函数
第三十章 二次函数
课时导入
我们已经学习了哪些函数?它们的解析式是什么?
回顾旧知
一次函数 y=kx+b(k≠0)
正比例函数 y=kx (k≠0)
反比例函数
一条直线
双曲线
课时导入
导入新知
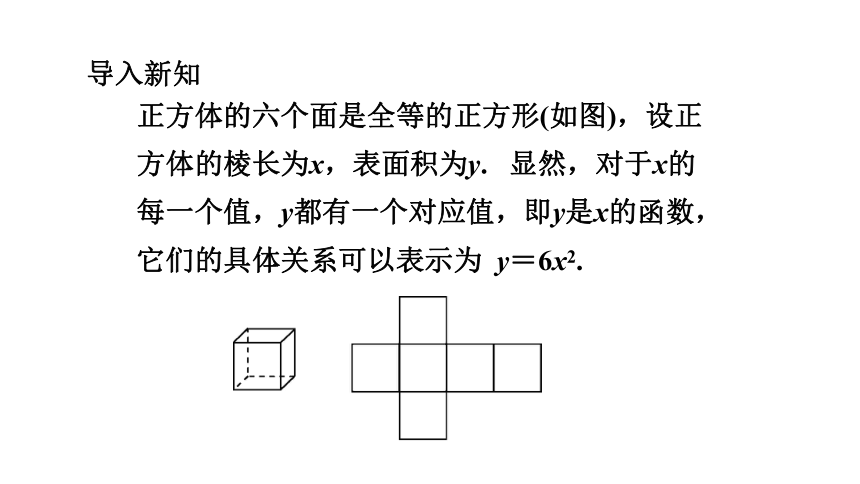
正方体的六个面是全等的正方形(如图),设正方体的棱长为x,表面积为y. 显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为 y=6x2.
课时导入
这个函数与我们学过的函数不同,其中自变
量x的最高次数是2.
这类函数具有哪些性质呢?这就是本章要学
习的二次函数.
知识点
二次函数的定义
知1-讲
感悟新知
1
1.如图所示,用规格相同的正方形瓷 砖铺成矩形地
面,其中,横向瓷砖比纵向瓷砖每排多 5块,矩
形地面最外面一圈
为灰色瓷砖,其余
部分全 为白色瓷砖.
设纵向每排有n块瓷
砖.
知1-讲
感悟新知
(1) 设灰色瓷砖的总数为y块.
用含n的代数式表示y;,
则y=_________.
② y与n具有怎样的函数关系?
设白色瓷砖的总数为z块.
①用含n的代数式表z,则z =__________.
② z是n的函数吗?说说理由.
n2 +n-6
4n+6
知1-讲
感悟新知
2.某企业今年第一季度的产值为80万元,预计产值
的季平均增长率为x.
(1)设第二季度的产值为y万元,则y=_________.
设第三季度的产值为z万元,则z=_______________.
(2) y, z都是x的函数吗?它们的表达式有什么不同?
80x+80
80x2+160x+80
知1-讲
感悟新知
思考:函数z=n2 +n-6,z=80x2+160x+80有
什么共同点?
1、函数解析式是整式;
2、化简后自变量的最高次数是2;
3、二次项系数不为0.
可以发现
知1-讲
感悟新知
一般地,形如y=ax2+bx+c(a,b,c是常数,
a≠0)的函数,叫做二次函数.其中,x是自变
量,a,b,c分别是函数解析式的二次项系数、
一次项系数和常数项.
定义
知1-讲
感悟新知
详解
二次函数的特殊形式:
1. 只含二次项, 即:y=ax2(b=0,c=0);
2. 不含一次项, 即:y=ax2+c(b=0,c ≠ 0);
3. 不含常数项, 即:y=ax2+bx(b ≠ 0,c=0).
感悟新知
知1-练
例 1
下列函数中,哪些是二次函数?并指出二次函
数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
感悟新知
知1-练
解:
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
(6)y=x2+
不是整式
×
感悟新知
知1-练
解:
二次项系数
二次项系数
一次项系数
常数项
(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
感悟新知
知1-练
1 下列函数表达式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2 下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
3 下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
C
B
知识点
二次函数的一般形式及函数值
知2-讲
感悟新知
2
一般地,任何一个二次函数,经过整理,都能化成如下形式:y=ax +bx+c0 (a≠0) 这种形式叫做二次函数的一般形式 .
为什么规定a≠0,b,c可以为0吗?
知2-讲
感悟新知
二次函数的项和各项系数
y=a x +b x+ c
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
指出方程各项的系数时要带上前面的符号.
知2-讲
感悟新知
函数值:确定一个x的值,代入二次函数表达式中
所得的y值为函数值.
感悟新知
知2-练
例2
当已知函数y=2x2-3x-2.
(1)当x=- 时,函数值为多少?
(2)当x为多少时,函数值为0.
(1)当x=- 时,
y=2× -3× -2=
(2)当y=0时,2x2-3x-2=0,
解得x1=2,x2=-
解:
知2-讲
总 结
感悟新知
求函数值及自变量的值,只要把对应的自变量x的值及函数值y代入函数表达式即可.
指出下列二次函数中相应的a,b,c的值:
知2-练
感悟新知
1
解:
(1)a=-5,b=3,c=1.
(2)y=(x+1)2-1=x2+2x,
∴a=1,b=2,c=0.
(3)a=-1,b=0,c=6.
知2-练
感悟新知
已知二次函数y=1-3x+5x2,则它的二次项系
数a,一次项系数b,常数项c分别是( )
A.a=1,b=-3,c=5
B.a=1,b=3,c=5
C.a=5,b=3,c=1
D.a=5,b=-3,c=1
2
D
知2-讲
感悟新知
a(地平线)
关于函数y=(500-10x)(40+x),下列说法不正确的是( )
A.y是x的二次函数
B.二次项系数是-10
C.一次项是100
D.常数项是20 000
3
C
知识点
利用二次函数的表达式表示实际问题
知3-讲
感悟新知
3
根据实际问题列二次函数的解析式,一般要经历
以下几个步骤:
(1)确定自变量与函数代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等
量关系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
感悟新知
a(地平线)
例 3
知3-练
某网店销售某款童装,每件售价为60元,每星期可卖300件.为了促销,该网店决定降价销售. 市场调查反映,每降价1元,每星期可多卖30件.已知该款童装每件成本价为40元,设该款童装每件售价为x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式,并写出自变量的取
值范围;
(2)设每星期的销售利润为W,求W与x之间的函数
关系式.
感悟新知
a(地平线)
知3-练
(1)销售量=基本部分+降价后多卖的件数;
(2)利用销售利润等于每件的利润乘销售量列
出利润与售价之间的关系,
导引:
(1)y=300+30(60-x)=-30x+2 100(0≤x≤40).
(2)依题意,得W=(x-40)( -30x+2 100)
=-30x2+3 300x-84 000.
解:
知3-讲
总 结
感悟新知
在实际问题中建立二次函数关系时,关键要扣住两个变量之间的等量关系,如本题的等量关系就是销售利润=单个利润× 销售量.这与一元二次方程中的等量关系是一致的.
知3-练
感悟新知
a(地平线)
一块长方形草地,它的长比宽多2 m. 设它的长为
x m,面积为 y m2,请写出用x表示y的函数表达式. y是x的二次函数吗?若是,请指出相应的a,b,c的值.
1
y=x·(x-2)=x2-2x.
y是x的二次函数.
a=1,b=-2,c=0.
解:
知3-练
感悟新知
a(地平线)
2 一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,则y与x之间的函数表达式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2
A
课堂小结
二次函数
1.关于二次函数的定义要理解三点:
(1)函数表达式必须是整式,自变量的取值是全体实
数,而在实际应用中,自变量的取值必须符合实
际意义.
(2)确定二次函数表达式的各项系数及常数项时,要
把函数表达式化为一般式.
(3)二次项系数不为0.
课堂小结
二次函数
2.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
第三十章 二次函数
第1节 二次函数
第三十章 二次函数
课时导入
我们已经学习了哪些函数?它们的解析式是什么?
回顾旧知
一次函数 y=kx+b(k≠0)
正比例函数 y=kx (k≠0)
反比例函数
一条直线
双曲线
课时导入
导入新知
正方体的六个面是全等的正方形(如图),设正方体的棱长为x,表面积为y. 显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为 y=6x2.
课时导入
这个函数与我们学过的函数不同,其中自变
量x的最高次数是2.
这类函数具有哪些性质呢?这就是本章要学
习的二次函数.
知识点
二次函数的定义
知1-讲
感悟新知
1
1.如图所示,用规格相同的正方形瓷 砖铺成矩形地
面,其中,横向瓷砖比纵向瓷砖每排多 5块,矩
形地面最外面一圈
为灰色瓷砖,其余
部分全 为白色瓷砖.
设纵向每排有n块瓷
砖.
知1-讲
感悟新知
(1) 设灰色瓷砖的总数为y块.
用含n的代数式表示y;,
则y=_________.
② y与n具有怎样的函数关系?
设白色瓷砖的总数为z块.
①用含n的代数式表z,则z =__________.
② z是n的函数吗?说说理由.
n2 +n-6
4n+6
知1-讲
感悟新知
2.某企业今年第一季度的产值为80万元,预计产值
的季平均增长率为x.
(1)设第二季度的产值为y万元,则y=_________.
设第三季度的产值为z万元,则z=_______________.
(2) y, z都是x的函数吗?它们的表达式有什么不同?
80x+80
80x2+160x+80
知1-讲
感悟新知
思考:函数z=n2 +n-6,z=80x2+160x+80有
什么共同点?
1、函数解析式是整式;
2、化简后自变量的最高次数是2;
3、二次项系数不为0.
可以发现
知1-讲
感悟新知
一般地,形如y=ax2+bx+c(a,b,c是常数,
a≠0)的函数,叫做二次函数.其中,x是自变
量,a,b,c分别是函数解析式的二次项系数、
一次项系数和常数项.
定义
知1-讲
感悟新知
详解
二次函数的特殊形式:
1. 只含二次项, 即:y=ax2(b=0,c=0);
2. 不含一次项, 即:y=ax2+c(b=0,c ≠ 0);
3. 不含常数项, 即:y=ax2+bx(b ≠ 0,c=0).
感悟新知
知1-练
例 1
下列函数中,哪些是二次函数?并指出二次函
数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
感悟新知
知1-练
解:
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
(6)y=x2+
不是整式
×
感悟新知
知1-练
解:
二次项系数
二次项系数
一次项系数
常数项
(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
感悟新知
知1-练
1 下列函数表达式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2 下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
3 下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
C
B
知识点
二次函数的一般形式及函数值
知2-讲
感悟新知
2
一般地,任何一个二次函数,经过整理,都能化成如下形式:y=ax +bx+c0 (a≠0) 这种形式叫做二次函数的一般形式 .
为什么规定a≠0,b,c可以为0吗?
知2-讲
感悟新知
二次函数的项和各项系数
y=a x +b x+ c
二次项系数
一次项系数
a≠0
二次项
一次项
常数项
指出方程各项的系数时要带上前面的符号.
知2-讲
感悟新知
函数值:确定一个x的值,代入二次函数表达式中
所得的y值为函数值.
感悟新知
知2-练
例2
当已知函数y=2x2-3x-2.
(1)当x=- 时,函数值为多少?
(2)当x为多少时,函数值为0.
(1)当x=- 时,
y=2× -3× -2=
(2)当y=0时,2x2-3x-2=0,
解得x1=2,x2=-
解:
知2-讲
总 结
感悟新知
求函数值及自变量的值,只要把对应的自变量x的值及函数值y代入函数表达式即可.
指出下列二次函数中相应的a,b,c的值:
知2-练
感悟新知
1
解:
(1)a=-5,b=3,c=1.
(2)y=(x+1)2-1=x2+2x,
∴a=1,b=2,c=0.
(3)a=-1,b=0,c=6.
知2-练
感悟新知
已知二次函数y=1-3x+5x2,则它的二次项系
数a,一次项系数b,常数项c分别是( )
A.a=1,b=-3,c=5
B.a=1,b=3,c=5
C.a=5,b=3,c=1
D.a=5,b=-3,c=1
2
D
知2-讲
感悟新知
a(地平线)
关于函数y=(500-10x)(40+x),下列说法不正确的是( )
A.y是x的二次函数
B.二次项系数是-10
C.一次项是100
D.常数项是20 000
3
C
知识点
利用二次函数的表达式表示实际问题
知3-讲
感悟新知
3
根据实际问题列二次函数的解析式,一般要经历
以下几个步骤:
(1)确定自变量与函数代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等
量关系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
感悟新知
a(地平线)
例 3
知3-练
某网店销售某款童装,每件售价为60元,每星期可卖300件.为了促销,该网店决定降价销售. 市场调查反映,每降价1元,每星期可多卖30件.已知该款童装每件成本价为40元,设该款童装每件售价为x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式,并写出自变量的取
值范围;
(2)设每星期的销售利润为W,求W与x之间的函数
关系式.
感悟新知
a(地平线)
知3-练
(1)销售量=基本部分+降价后多卖的件数;
(2)利用销售利润等于每件的利润乘销售量列
出利润与售价之间的关系,
导引:
(1)y=300+30(60-x)=-30x+2 100(0≤x≤40).
(2)依题意,得W=(x-40)( -30x+2 100)
=-30x2+3 300x-84 000.
解:
知3-讲
总 结
感悟新知
在实际问题中建立二次函数关系时,关键要扣住两个变量之间的等量关系,如本题的等量关系就是销售利润=单个利润× 销售量.这与一元二次方程中的等量关系是一致的.
知3-练
感悟新知
a(地平线)
一块长方形草地,它的长比宽多2 m. 设它的长为
x m,面积为 y m2,请写出用x表示y的函数表达式. y是x的二次函数吗?若是,请指出相应的a,b,c的值.
1
y=x·(x-2)=x2-2x.
y是x的二次函数.
a=1,b=-2,c=0.
解:
知3-练
感悟新知
a(地平线)
2 一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,则y与x之间的函数表达式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2
A
课堂小结
二次函数
1.关于二次函数的定义要理解三点:
(1)函数表达式必须是整式,自变量的取值是全体实
数,而在实际应用中,自变量的取值必须符合实
际意义.
(2)确定二次函数表达式的各项系数及常数项时,要
把函数表达式化为一般式.
(3)二次项系数不为0.
课堂小结
二次函数
2.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
