冀教版七年级数学上册课件 1.2 数轴(15张)
文档属性
| 名称 | 冀教版七年级数学上册课件 1.2 数轴(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 14:31:53 | ||
图片预览



文档简介
(共15张PPT)
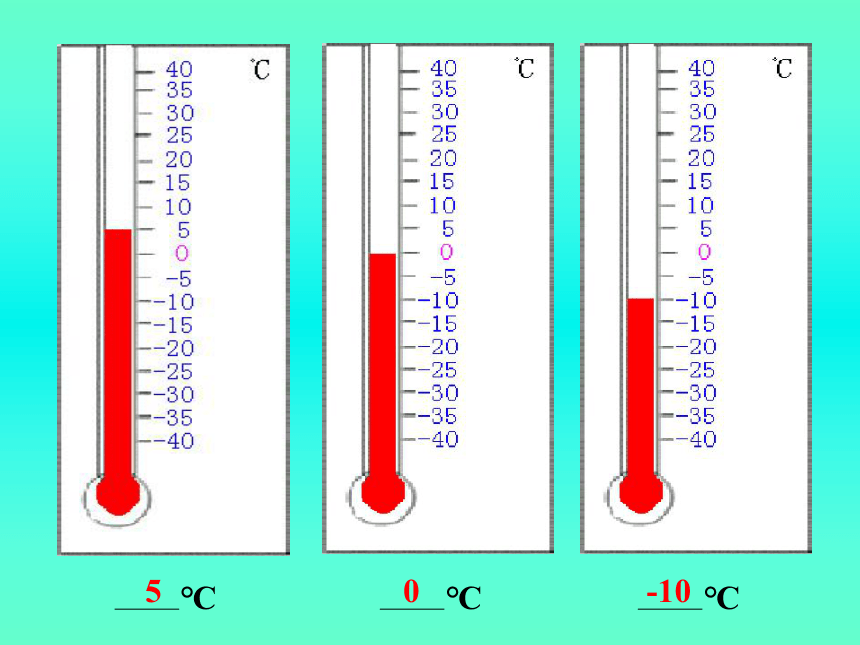
℃
℃
℃
5
0
-10
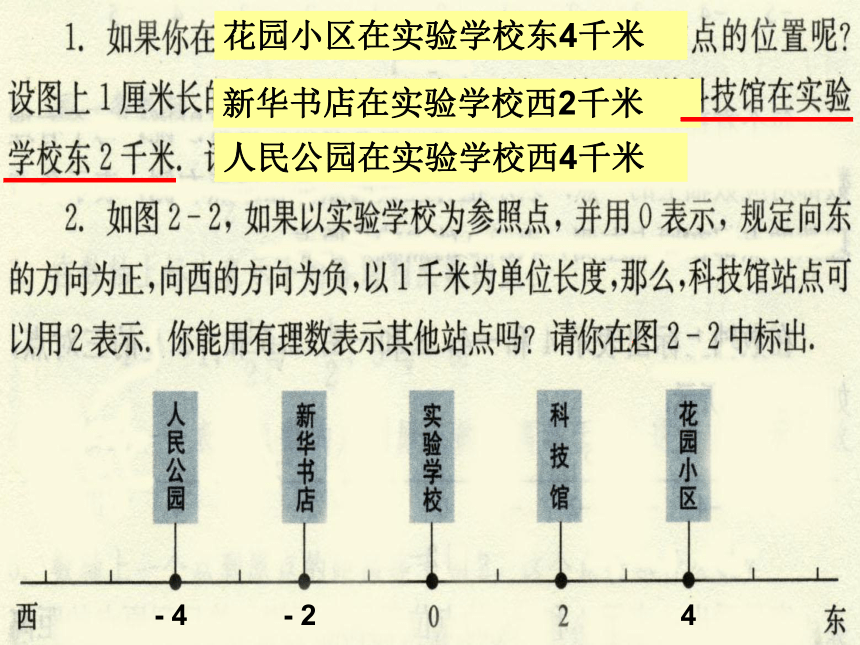
4
- 2
- 4
花园小区在实验学校东4千米
新华书店在实验学校西2千米
人民公园在实验学校西4千米
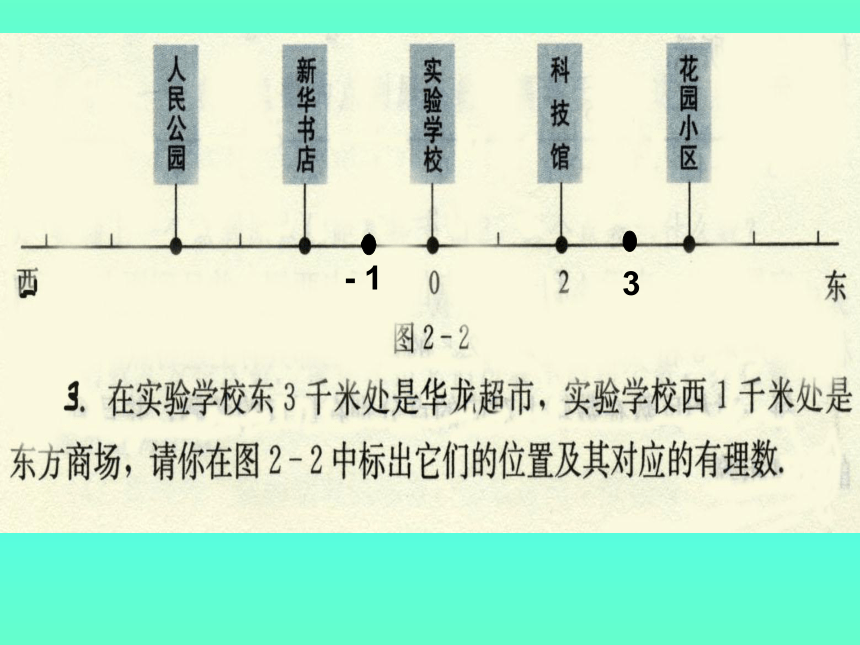
3
- 1
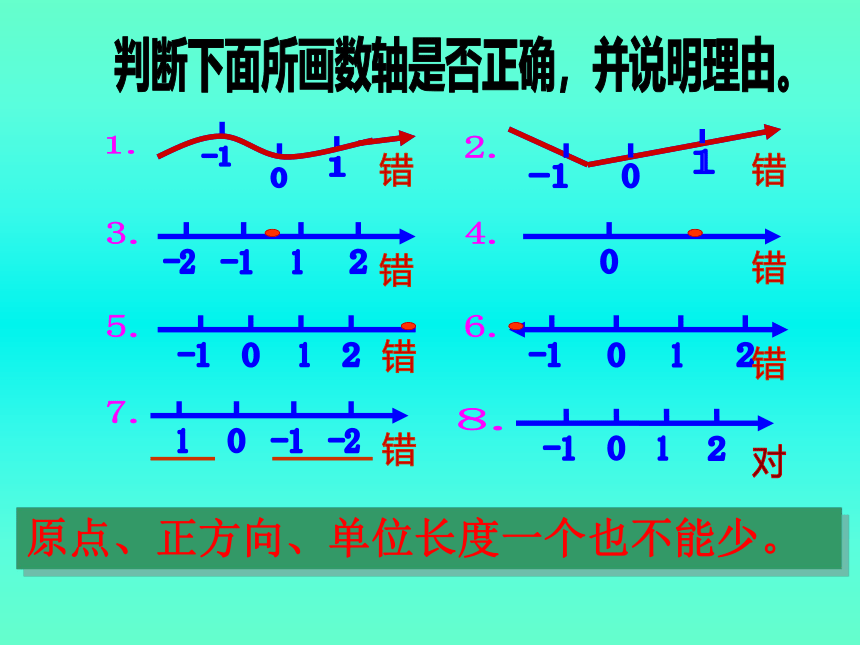
规定了原点,正方向和单位长度的直线,
叫做数轴
原点、正方向、单位长度一个也不能少。
A: - 4
B: - 1
C: 0
D: 3
0
1
2
3
-1
-2
-3
-4
4
-1.5
1|4
任何一个有理数都可以用数轴上的一个点来表示。
在数轴上表示下列各数
1|4
+3,-4,
,1.5
-4
+3
规定了原点,正方向和单位长度的直线,
叫做数轴
数轴的三要素
在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
0
1
2
3
解:
1. 画出数轴,并用数轴上的点表示下列各数:
3|2
- 5,0,5,- 4,
-
3|2
,4
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
- 5
0
5
- 4
4
6个单位
左
右
2个单位
2填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点
的 侧,距原点的距离是 。
数轴上的两个点,右边点表示的数与左边点表示的数的大小关系?
0
1
2
3
-1
-2
-3
数轴上两个点表示的数,右边的总比左边的大。
负数小于0,
正数大于负数。
正数大于0,
越来越大
例3 比较下列每组数的大小:
(1)-2和+6; (2) 0 和-1.8; (3)
-
3|2
和-4;
解: (1)-2<+6
(正数大于负数);
(2)0>-1.8
(负数小于零);
(3)
-
3|2
>-4
(数轴上,
-
3|2
所对应的点在-4
所对应点的右侧)。
一填空
(1)-8的相反数是( ),( )相反数是-
3|4
.
(2)数轴上表示-2的点在原点的( )侧,距原点的
距离是( ),表示-6的点在原点的( )侧,距
原点的距离是( )。
二判断
(1)0没有相反数。( )
(2)符号不相同的两个数互为相反数( )
(3)数轴上的两个点可以表示同一个有理数( )
8
3|4
左
2
左
6
X
X
X
(4) 数轴上的点都表示整数。 ( )
X
(5)数轴上的点只能表示正数和零。 ( )
X
思考题:
一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢?如果按上面的移动规律,最后得到的点表示的数是2,则开始时它表示什么数?
答:它表示的数是
- 2
按上面的移动规律,最后得到的点表示的数是2,
则开始时它表示的数是 -1
任何一个有理数都可以用数轴上
的一个点来表示。
正方向
数轴的三要素
单位长度
原点
数轴的引入,使我们能用直观图形来解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
℃
℃
℃
5
0
-10
4
- 2
- 4
花园小区在实验学校东4千米
新华书店在实验学校西2千米
人民公园在实验学校西4千米
3
- 1
规定了原点,正方向和单位长度的直线,
叫做数轴
原点、正方向、单位长度一个也不能少。
A: - 4
B: - 1
C: 0
D: 3
0
1
2
3
-1
-2
-3
-4
4
-1.5
1|4
任何一个有理数都可以用数轴上的一个点来表示。
在数轴上表示下列各数
1|4
+3,-4,
,1.5
-4
+3
规定了原点,正方向和单位长度的直线,
叫做数轴
数轴的三要素
在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
0
1
2
3
解:
1. 画出数轴,并用数轴上的点表示下列各数:
3|2
- 5,0,5,- 4,
-
3|2
,4
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
- 5
0
5
- 4
4
6个单位
左
右
2个单位
2填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点
的 侧,距原点的距离是 。
数轴上的两个点,右边点表示的数与左边点表示的数的大小关系?
0
1
2
3
-1
-2
-3
数轴上两个点表示的数,右边的总比左边的大。
负数小于0,
正数大于负数。
正数大于0,
越来越大
例3 比较下列每组数的大小:
(1)-2和+6; (2) 0 和-1.8; (3)
-
3|2
和-4;
解: (1)-2<+6
(正数大于负数);
(2)0>-1.8
(负数小于零);
(3)
-
3|2
>-4
(数轴上,
-
3|2
所对应的点在-4
所对应点的右侧)。
一填空
(1)-8的相反数是( ),( )相反数是-
3|4
.
(2)数轴上表示-2的点在原点的( )侧,距原点的
距离是( ),表示-6的点在原点的( )侧,距
原点的距离是( )。
二判断
(1)0没有相反数。( )
(2)符号不相同的两个数互为相反数( )
(3)数轴上的两个点可以表示同一个有理数( )
8
3|4
左
2
左
6
X
X
X
(4) 数轴上的点都表示整数。 ( )
X
(5)数轴上的点只能表示正数和零。 ( )
X
思考题:
一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢?如果按上面的移动规律,最后得到的点表示的数是2,则开始时它表示什么数?
答:它表示的数是
- 2
按上面的移动规律,最后得到的点表示的数是2,
则开始时它表示的数是 -1
任何一个有理数都可以用数轴上
的一个点来表示。
正方向
数轴的三要素
单位长度
原点
数轴的引入,使我们能用直观图形来解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
