冀教版七年级数学上册 1.3 绝对值与相反数课件(23张ppt)
文档属性
| 名称 | 冀教版七年级数学上册 1.3 绝对值与相反数课件(23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 16:35:12 | ||
图片预览




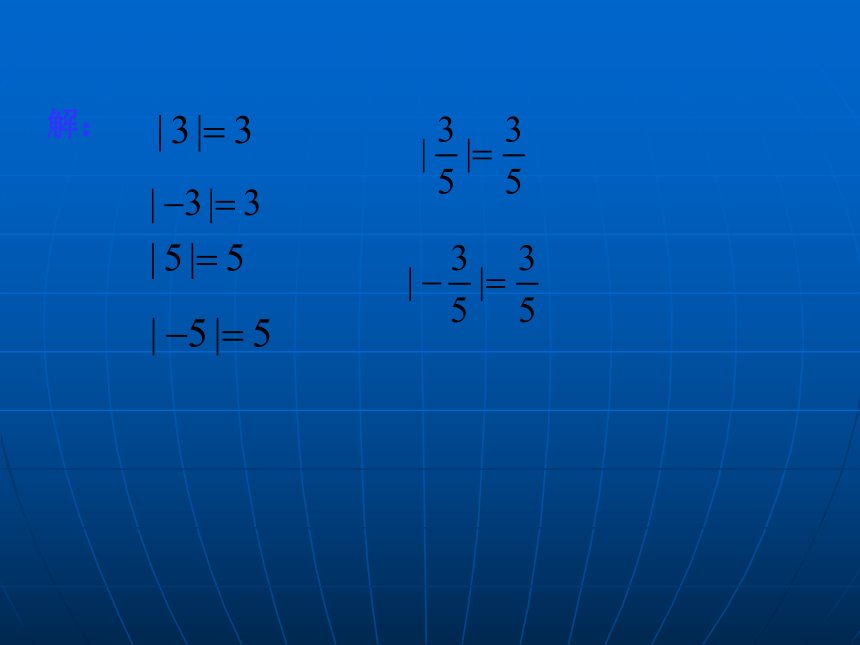
文档简介
(共23张PPT)
1.借助数轴理解绝对值、相反数的概念,能准确熟练地求一个有理数的绝对值、相反数.
2.通过探索正数、负数及0的绝对值和相反数的过程,初步培养学生观察、分析、归纳和概括的思维能力.
3.通过本课的学习向学生渗透数形结合思想和分类讨论的思想.
教学重点:绝对值、相反数的意义以及求一个数的绝对值、相反数.
教学难点:求一个负数的绝对值、相反数.
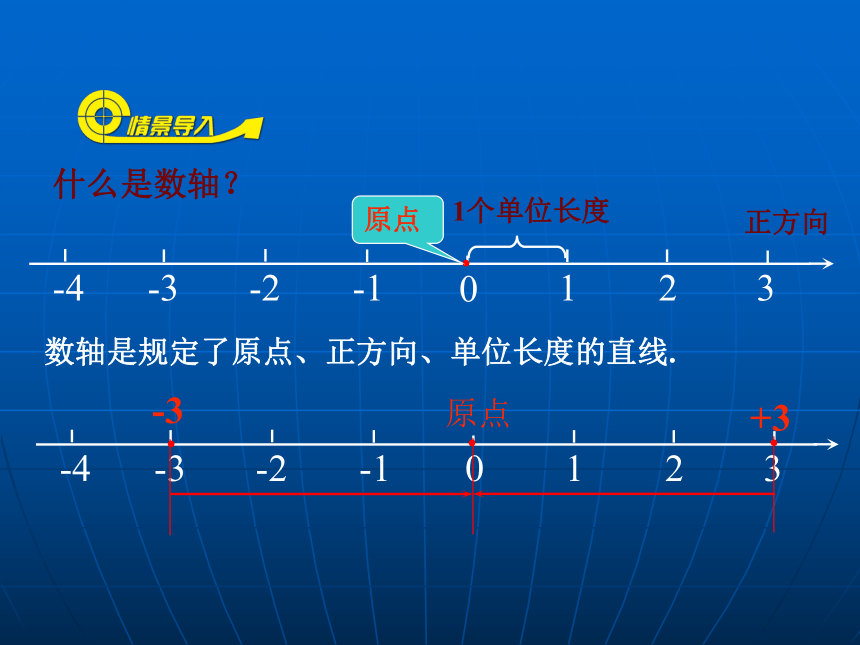
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线.
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
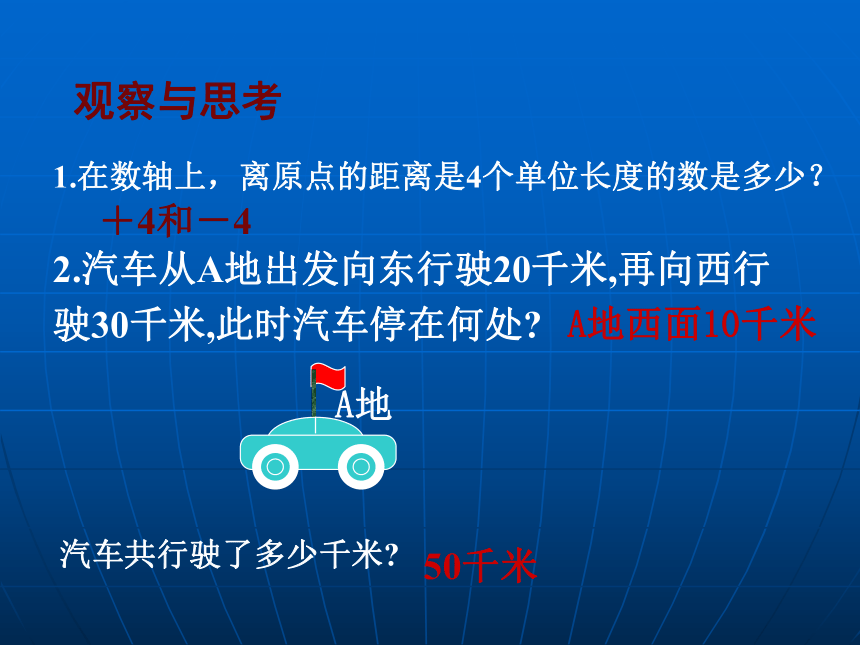
1.在数轴上,离原点的距离是4个单位长度的数是多少?
+4和-4
汽车共行驶了多少千米
观察与思考
2.汽车从A地出发向东行驶20千米,再向西行驶30千米,此时汽车停在何处
A地西面10千米
50千米
A地
1、画出数轴,在数轴上表示下列各数,并写出这些点到原点的距离.
-5,0,5,-4,- .
,
做一做
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.
绝对值的概念
答案:
到原点距离
,5,0,5,4, .
2/3
2/3
2/3
-2/3
表示4 的点到原点的距离是 ( )
4
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
4
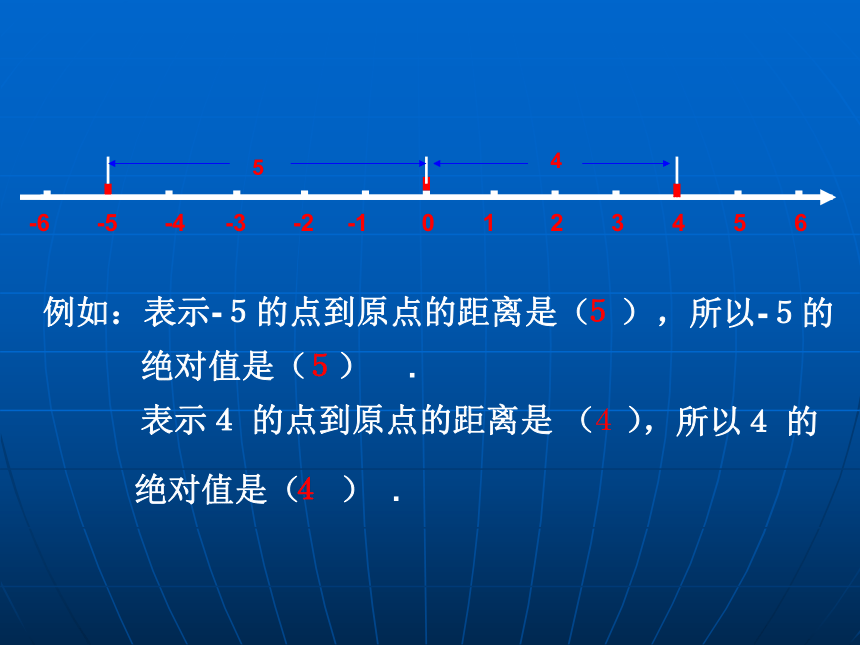
例如:表示-5的点到原点的距离是( )
,所以-5的
5
绝对值是( ) .
5
,所以4 的
4
绝对值是( ) .
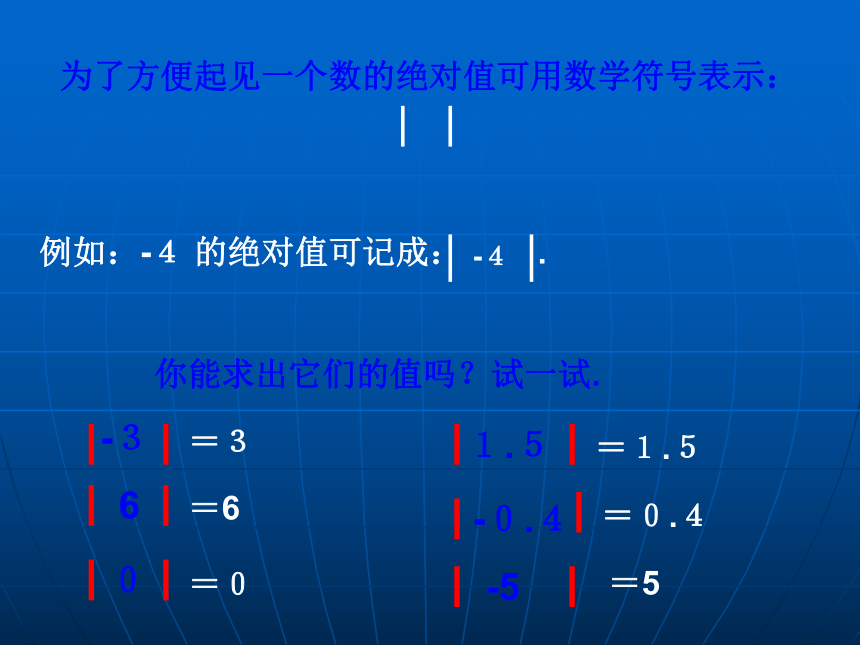
为了方便起见一个数的绝对值可用数学符号表示:
例如:-4 的绝对值可记成: .
-4
1.5
-3
-0.4
0
6
-5
你能求出它们的值吗?试一试.
=3
=6
=0
=1.5
=0.4
=5
例1:用数轴上的点表示下列各组数:
①3,-3 ②5,-5 ③ .
例题学习 强化概念
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
观察表示上述各组数的点在数轴上的位置,写出这些数的绝对值:
解:
观察例1中的三组数在数轴上的位置和绝对值的大小,说说这三组数的共同特点是什么?
像3和-3 ,5和-5 , 等这样符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.0的相反数规定为0.
观察与思考
互为相反数的两个数的绝对值有什么关系
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零;
任意一个有理数的绝对值是一个非负数.
一个数的绝对值与这个数有什么关系
例2:化简下列各数:
-(-11),-(+2),-(-3.75),-(+ ).
例题学习 强化概念
解:因为-11的相反数是11,所以-(-11)=11.
因为+2的相反数是-2,所以-(+2)=-2.
同理,-(-3.75)=3.75,-(+ )=- .
一般地,a和-a互为相反数.
特别地,0的相反数是0.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
归纳总结:
(1)当a>0时,
a =
(2)当a<0时,
a =
(3)当a=0时,
a =
a.
-a.
0.
总结:任何一个数的绝对值一定是非负数.
| 5-1 | = ( )
4
1 + | -5 | =( )
6
| 5 | - | -3 | =( )
| -1 | + | -2 | =( )
2
3
| +3 | - | -3 | =( )
0
| +3 | = | -3 | = 3
填一填.
分层练习,形成能力
(2)绝对值小于 10 的整数有( )个.
(3)绝对值不大于 7 的负整数是( ).
(1)绝对值等于4的数是( ).
+4, -4
19
-1,-2,-3,-4,-5,-6,-7
(4)绝对值大于 而小于 的整数是
( ).
2
3
8
3
+1,-1,+2,-2
(1)一个数的绝对值一定是正数. ( )
(2)一个数的绝对值不可能是负数. ( )
(3)互为相反数的两个数,它们的绝对值
一定相等. ( )
(4)绝对值是同一个正数的数有两个,且
它们是互为相反数. ( )
×
√
√
√
⑴绝对值相等,符号相反的两个数( );
⑵( )相等的两个数在数轴上的对应点到
原点距离相等.
互为相反数
绝对值
(1) m 是有理数时,下列说法中正确的是( )
(A) -m 是负数 (B) |m|是正数
(C) |-m|是非负数 (D) -|m|是负数
(2)若 |a| > a , 则 a 是( )
(A)正数 (B)负数
(C)非正数 (D)非负数
(3)一个数的相反数的绝对值是正数,这个数一定是( )
(A)非正数 (B)非负数
(C)非零数 (D)不能确定
C
B
C
文字叙述 表达式叙述
一个数的绝对值是它本身,这个数是( ).
正数或零
一个数的绝对值是它的相反数,这个数是( ).
负数或零
如果 | a | = a , a ≥0 .
如果 | a | = -a , a ≤ 0 .
| a | =
( a > 0 )
a
( a < 0 )
-a
( a = 0 )
0
{
a的绝对值
本节课学习了以下内容:
1.求一个数的绝对值,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
2.相反数的概念:只有符号不同的两个数,我们说其中一个数是另一个数的相反数.
例如: 表示数 的相反数.
小 结
1.借助数轴理解绝对值、相反数的概念,能准确熟练地求一个有理数的绝对值、相反数.
2.通过探索正数、负数及0的绝对值和相反数的过程,初步培养学生观察、分析、归纳和概括的思维能力.
3.通过本课的学习向学生渗透数形结合思想和分类讨论的思想.
教学重点:绝对值、相反数的意义以及求一个数的绝对值、相反数.
教学难点:求一个负数的绝对值、相反数.
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线.
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
1.在数轴上,离原点的距离是4个单位长度的数是多少?
+4和-4
汽车共行驶了多少千米
观察与思考
2.汽车从A地出发向东行驶20千米,再向西行驶30千米,此时汽车停在何处
A地西面10千米
50千米
A地
1、画出数轴,在数轴上表示下列各数,并写出这些点到原点的距离.
-5,0,5,-4,- .
,
做一做
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.
绝对值的概念
答案:
到原点距离
,5,0,5,4, .
2/3
2/3
2/3
-2/3
表示4 的点到原点的距离是 ( )
4
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
4
例如:表示-5的点到原点的距离是( )
,所以-5的
5
绝对值是( ) .
5
,所以4 的
4
绝对值是( ) .
为了方便起见一个数的绝对值可用数学符号表示:
例如:-4 的绝对值可记成: .
-4
1.5
-3
-0.4
0
6
-5
你能求出它们的值吗?试一试.
=3
=6
=0
=1.5
=0.4
=5
例1:用数轴上的点表示下列各组数:
①3,-3 ②5,-5 ③ .
例题学习 强化概念
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
观察表示上述各组数的点在数轴上的位置,写出这些数的绝对值:
解:
观察例1中的三组数在数轴上的位置和绝对值的大小,说说这三组数的共同特点是什么?
像3和-3 ,5和-5 , 等这样符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.0的相反数规定为0.
观察与思考
互为相反数的两个数的绝对值有什么关系
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零;
任意一个有理数的绝对值是一个非负数.
一个数的绝对值与这个数有什么关系
例2:化简下列各数:
-(-11),-(+2),-(-3.75),-(+ ).
例题学习 强化概念
解:因为-11的相反数是11,所以-(-11)=11.
因为+2的相反数是-2,所以-(+2)=-2.
同理,-(-3.75)=3.75,-(+ )=- .
一般地,a和-a互为相反数.
特别地,0的相反数是0.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
归纳总结:
(1)当a>0时,
a =
(2)当a<0时,
a =
(3)当a=0时,
a =
a.
-a.
0.
总结:任何一个数的绝对值一定是非负数.
| 5-1 | = ( )
4
1 + | -5 | =( )
6
| 5 | - | -3 | =( )
| -1 | + | -2 | =( )
2
3
| +3 | - | -3 | =( )
0
| +3 | = | -3 | = 3
填一填.
分层练习,形成能力
(2)绝对值小于 10 的整数有( )个.
(3)绝对值不大于 7 的负整数是( ).
(1)绝对值等于4的数是( ).
+4, -4
19
-1,-2,-3,-4,-5,-6,-7
(4)绝对值大于 而小于 的整数是
( ).
2
3
8
3
+1,-1,+2,-2
(1)一个数的绝对值一定是正数. ( )
(2)一个数的绝对值不可能是负数. ( )
(3)互为相反数的两个数,它们的绝对值
一定相等. ( )
(4)绝对值是同一个正数的数有两个,且
它们是互为相反数. ( )
×
√
√
√
⑴绝对值相等,符号相反的两个数( );
⑵( )相等的两个数在数轴上的对应点到
原点距离相等.
互为相反数
绝对值
(1) m 是有理数时,下列说法中正确的是( )
(A) -m 是负数 (B) |m|是正数
(C) |-m|是非负数 (D) -|m|是负数
(2)若 |a| > a , 则 a 是( )
(A)正数 (B)负数
(C)非正数 (D)非负数
(3)一个数的相反数的绝对值是正数,这个数一定是( )
(A)非正数 (B)非负数
(C)非零数 (D)不能确定
C
B
C
文字叙述 表达式叙述
一个数的绝对值是它本身,这个数是( ).
正数或零
一个数的绝对值是它的相反数,这个数是( ).
负数或零
如果 | a | = a , a ≥0 .
如果 | a | = -a , a ≤ 0 .
| a | =
( a > 0 )
a
( a < 0 )
-a
( a = 0 )
0
{
a的绝对值
本节课学习了以下内容:
1.求一个数的绝对值,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
2.相反数的概念:只有符号不同的两个数,我们说其中一个数是另一个数的相反数.
例如: 表示数 的相反数.
小 结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
