冀教版七年级数学上册课件 4.2 合并同类项(共23张PPT)
文档属性
| 名称 | 冀教版七年级数学上册课件 4.2 合并同类项(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 19:52:35 | ||
图片预览





文档简介
(共23张PPT)
第1课时 合并同类项
七年级数学 上册
+
=
= 3
4
―
6
一、创设情境,引入课题
+
=
创设情境,引入课题
引入
问题1:在西宁到拉萨路段,列车在冻土地
段的行驶速度是100 km/h,在非冻土地段的
行驶速度是120 km/h,列车通过非冻土地段
所需时间是通过冻土地段所需时间的2.1倍 ,
如果通过冻土地段需要t h,你能用含t的式子
表示这段铁路的全长吗?
学习目标:
(1)理解同类项的概念;
(2)掌握合并同类项的方法;
(3)通过类比数的运算探究合并同类项的法则,从中体会数式通性和类比的数学思想.
二、出示目标、点明主旨
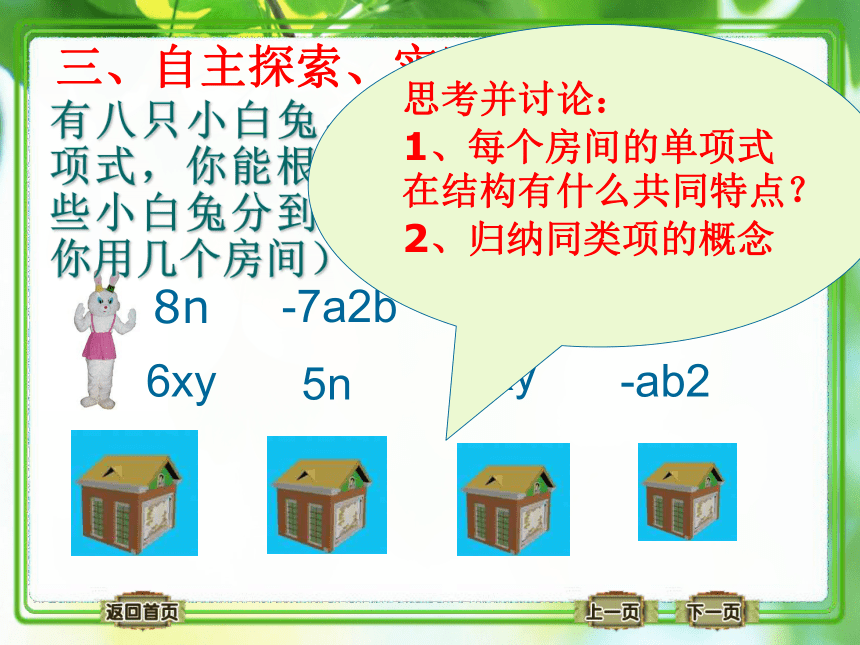
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
三、自主探索、实践新知
思考并讨论:
1、每个房间的单项式在结构有什么共同特点?
2、归纳同类项的概念
1.同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
下列各组中的两项是不是同类项?
注意:(1) 同类项与系数无关,与字母的排列顺序也无关(两相同、两无关)。
(2)几个常数项也是同类项。
4
+ =
6
―
= 3
4a 2a
6
4x x =
3x
a
a
a
什么是乘法分配律?用字母式子如何表示?
运用有理数的运算律计算:
100×2+252×2=
100×(-2)+252×(-2)=
思考:
有理数可以进行加减运算,那么整式能否可以加减运算呢?怎样化简呢?
例如:
(1)100t—252t=
(2)3x2 + 2 x2 =
(3)3ab2 - 4 ab2=
四、合作探究、再探新知
1、具备什么特点的多项式可以合并呢?
2、合并同类项的定义?
3、合并后什么变了,什么又没有变?(合并同类项的法则)
-152t
5x2
- ab2
把多项式中的同类项合并成一项叫合并同类项.
2.合并同类项的定义:
合并同类项的 :
①合并同类项的实质是乘法分配律的逆应用,如3a+4a=(3+4)a=7a;
②“一变”、“两不变”,即系数相加——变,字母和字母的指数——保持不变;
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
试一试.
合并下列各式的同类项:
(1)3x3+x3; (2)xy2- xy2.
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2- xy2
=(1- )xy2
= xy2
类比探究,学习新知
例
找出多项式中的同类项并进行合并,
思考下面问题:
每一步运算的依据是什么?注意什么?
类比探究,学习新知
例题
解:
( 交换律 )
( 结合律 )
( 分配律 )
(按字母的指数从大到
小顺序排列)
合并同类项 注意:
①一找,二移,三和,四算。
②多项式中只有同类项才能合并,不是同类项不能
合并.
③通常我们把一个多项式的各项按照某个字母的指
数从大到小(降幂)或者从小到大(升幂)的顺
序排列,如:-4x2+5x+5或写5+5x-4x2.
归纳步骤:
(1)找出同类项并做标记;
(2)运用交换律、结合律将多项式的同类项结合;
(3)合并同类项;
(4)按同一个字母的降幂(或升幂排列).
学以致用,应用新知
合并下列各式的同类项:
(1)
(2)
(3)
(1)求多项式
的值,其中
(2)求多项式
的值,其中
(1)水库水位第一天连续下降了a h,每小时平均下降2 cm;第二天连续上升了a h,每小时平均上升0.5 cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x kg,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解:由题意得2a-0.5a=1.5a,所以这两天水位总的下降了1.5a
解:由题意得:5x-3x+4x=6x
所以进货后这个商店有大米6x千克
(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?
六、小结归纳,自我完善
课堂检测
判断下列说法是否正确,正确的
在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )
下列运算,正确的是 (填序号)
① ②
③ ④
第1课时 合并同类项
七年级数学 上册
+
=
= 3
4
―
6
一、创设情境,引入课题
+
=
创设情境,引入课题
引入
问题1:在西宁到拉萨路段,列车在冻土地
段的行驶速度是100 km/h,在非冻土地段的
行驶速度是120 km/h,列车通过非冻土地段
所需时间是通过冻土地段所需时间的2.1倍 ,
如果通过冻土地段需要t h,你能用含t的式子
表示这段铁路的全长吗?
学习目标:
(1)理解同类项的概念;
(2)掌握合并同类项的方法;
(3)通过类比数的运算探究合并同类项的法则,从中体会数式通性和类比的数学思想.
二、出示目标、点明主旨
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
三、自主探索、实践新知
思考并讨论:
1、每个房间的单项式在结构有什么共同特点?
2、归纳同类项的概念
1.同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
下列各组中的两项是不是同类项?
注意:(1) 同类项与系数无关,与字母的排列顺序也无关(两相同、两无关)。
(2)几个常数项也是同类项。
4
+ =
6
―
= 3
4a 2a
6
4x x =
3x
a
a
a
什么是乘法分配律?用字母式子如何表示?
运用有理数的运算律计算:
100×2+252×2=
100×(-2)+252×(-2)=
思考:
有理数可以进行加减运算,那么整式能否可以加减运算呢?怎样化简呢?
例如:
(1)100t—252t=
(2)3x2 + 2 x2 =
(3)3ab2 - 4 ab2=
四、合作探究、再探新知
1、具备什么特点的多项式可以合并呢?
2、合并同类项的定义?
3、合并后什么变了,什么又没有变?(合并同类项的法则)
-152t
5x2
- ab2
把多项式中的同类项合并成一项叫合并同类项.
2.合并同类项的定义:
合并同类项的 :
①合并同类项的实质是乘法分配律的逆应用,如3a+4a=(3+4)a=7a;
②“一变”、“两不变”,即系数相加——变,字母和字母的指数——保持不变;
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
试一试.
合并下列各式的同类项:
(1)3x3+x3; (2)xy2- xy2.
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2- xy2
=(1- )xy2
= xy2
类比探究,学习新知
例
找出多项式中的同类项并进行合并,
思考下面问题:
每一步运算的依据是什么?注意什么?
类比探究,学习新知
例题
解:
( 交换律 )
( 结合律 )
( 分配律 )
(按字母的指数从大到
小顺序排列)
合并同类项 注意:
①一找,二移,三和,四算。
②多项式中只有同类项才能合并,不是同类项不能
合并.
③通常我们把一个多项式的各项按照某个字母的指
数从大到小(降幂)或者从小到大(升幂)的顺
序排列,如:-4x2+5x+5或写5+5x-4x2.
归纳步骤:
(1)找出同类项并做标记;
(2)运用交换律、结合律将多项式的同类项结合;
(3)合并同类项;
(4)按同一个字母的降幂(或升幂排列).
学以致用,应用新知
合并下列各式的同类项:
(1)
(2)
(3)
(1)求多项式
的值,其中
(2)求多项式
的值,其中
(1)水库水位第一天连续下降了a h,每小时平均下降2 cm;第二天连续上升了a h,每小时平均上升0.5 cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x kg,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解:由题意得2a-0.5a=1.5a,所以这两天水位总的下降了1.5a
解:由题意得:5x-3x+4x=6x
所以进货后这个商店有大米6x千克
(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?
六、小结归纳,自我完善
课堂检测
判断下列说法是否正确,正确的
在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )
下列运算,正确的是 (填序号)
① ②
③ ④
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
