苏科版八年级数学上册 2.4 线段、角的轴对称性课件(16张)
文档属性
| 名称 | 苏科版八年级数学上册 2.4 线段、角的轴对称性课件(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-18 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
线段、角的轴对称性
在一张薄纸上画 ∠AOB,操作并思考:
它是轴对称图形吗? 为什么?
【做一做】
角是轴对称图形,它的对称轴在哪里?为什么?
O
A
B
角是轴对称图形,角平分线所在的直线是它的对称轴.
1.在∠AOB的角平分线OC任意取一点P,分别作出点P到OA、OB的距离,对折一下,你发现了什么?
【想一想】
B
C
D
E
已知:如图,在∠AOB的角平分线OC任意取一点P,PD⊥OA,PE⊥OB.
求证:PD=PE.
O
A
P
2.像这样的点P还有吗?
∵点P在角平分线OC上,
PD⊥OA,PE ⊥OB,
∴PD=PE .
定理 角平分线上的点到角两边的距离相等.
O
A
B
C
P
D
E
下图中PD=PE吗?
在上面的结论中,由条件: (1)OC是∠AOB的平分线,点P在OC上; (2)PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.
O
D
E
A
B
P
C
O
D
E
A
B
P
C
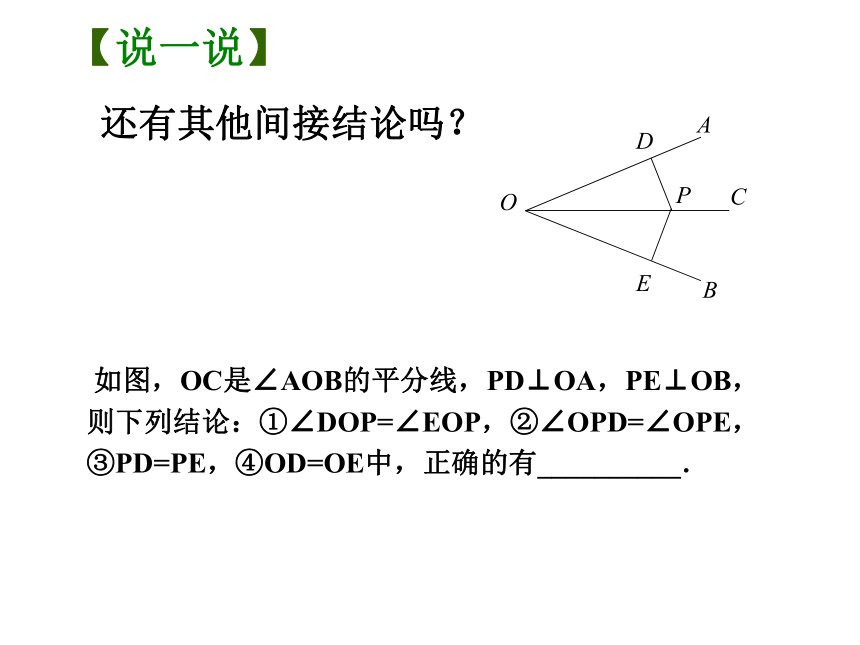
还有其他间接结论吗?
【说一说】
O
A
B
C
P
D
E
如图,OC是∠AOB的平分线,PD⊥OA,PE⊥OB,则下列结论:①∠DOP=∠EOP,②∠OPD=∠OPE,③PD=PE,④OD=OE中,正确的有__________.
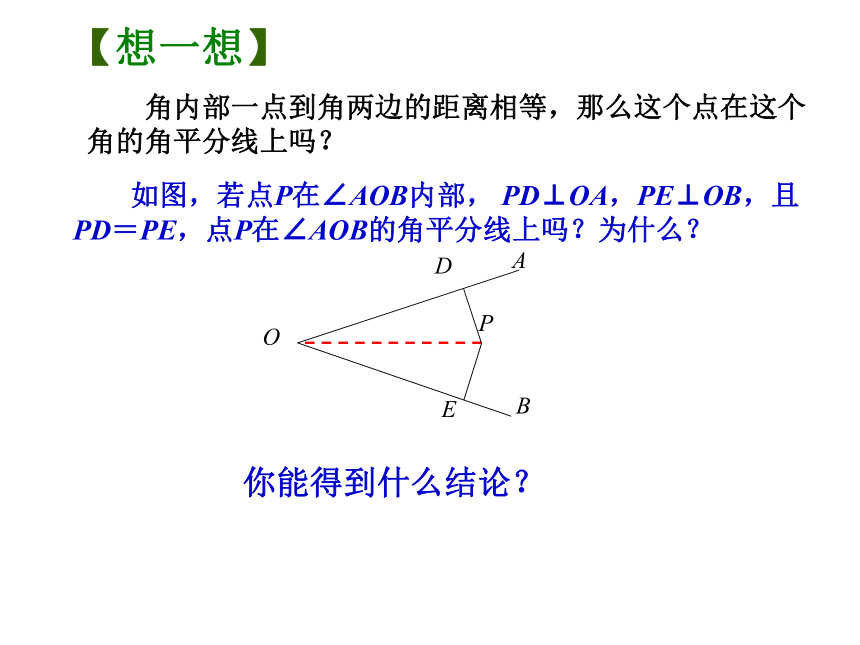
角内部一点到角两边的距离相等,那么这个点在这个角的角平分线上吗?
O
A
B
P
D
E
如图,若点P在∠AOB内部, PD⊥OA,PE⊥OB,且PD=PE,点P在∠AOB的角平分线上吗?为什么?
你能得到什么结论?
【想一想】
∵ PD⊥OA,PE ⊥OB,
PD=PE ,
∴点P在角平分线AC上 .
定理 角的内部到角两边的距离相等的点在角的平分线上.
O
A
B
C
P
D
E
角平分线是到角两边距离相等的点的集合.
1.如图,OC是∠AOB的平分线,PD⊥DA于点D,PD=5,则P点到OB的距离是_____.
【做一做 】
2.如图,在△ABC中,∠B=90°,BC=10,∠BAC的角平分线AD交BC于点D,BD:DC=2:3,则点D到AC的距离是________.
【做一做 】
3.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,交AB于点E,交AC于点F,若S△ABC=7,DE=2,AB=4,则AC=_____.
【做一做 】
4.在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB的垂直平分线分别交AC、AB于D、E两点.且DE=1cm,BD=2cm.则AC的长为_________cm.
【做一做 】
已知∠AOB和C、D两点,请在图中标出一点E,使得点E到OA、OB的距离相等,而且E点到C、D的距离也相等。
O
B
A
C
D
·
·
E
做一做
思考:已知:在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、AC上,且DE=DF.试判断∠BED与∠BFD的关系,并说明理由.
F
B
A
C
D
E
M
N
已知:在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、AC上,且DE=DF.试判断∠BED与∠BFD的关系,并说明理由.
变式:
F
B
A
C
D
M
N
E
说说你本节课你有什么收获?
【课堂小结 】
线段、角的轴对称性
在一张薄纸上画 ∠AOB,操作并思考:
它是轴对称图形吗? 为什么?
【做一做】
角是轴对称图形,它的对称轴在哪里?为什么?
O
A
B
角是轴对称图形,角平分线所在的直线是它的对称轴.
1.在∠AOB的角平分线OC任意取一点P,分别作出点P到OA、OB的距离,对折一下,你发现了什么?
【想一想】
B
C
D
E
已知:如图,在∠AOB的角平分线OC任意取一点P,PD⊥OA,PE⊥OB.
求证:PD=PE.
O
A
P
2.像这样的点P还有吗?
∵点P在角平分线OC上,
PD⊥OA,PE ⊥OB,
∴PD=PE .
定理 角平分线上的点到角两边的距离相等.
O
A
B
C
P
D
E
下图中PD=PE吗?
在上面的结论中,由条件: (1)OC是∠AOB的平分线,点P在OC上; (2)PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.
O
D
E
A
B
P
C
O
D
E
A
B
P
C
还有其他间接结论吗?
【说一说】
O
A
B
C
P
D
E
如图,OC是∠AOB的平分线,PD⊥OA,PE⊥OB,则下列结论:①∠DOP=∠EOP,②∠OPD=∠OPE,③PD=PE,④OD=OE中,正确的有__________.
角内部一点到角两边的距离相等,那么这个点在这个角的角平分线上吗?
O
A
B
P
D
E
如图,若点P在∠AOB内部, PD⊥OA,PE⊥OB,且PD=PE,点P在∠AOB的角平分线上吗?为什么?
你能得到什么结论?
【想一想】
∵ PD⊥OA,PE ⊥OB,
PD=PE ,
∴点P在角平分线AC上 .
定理 角的内部到角两边的距离相等的点在角的平分线上.
O
A
B
C
P
D
E
角平分线是到角两边距离相等的点的集合.
1.如图,OC是∠AOB的平分线,PD⊥DA于点D,PD=5,则P点到OB的距离是_____.
【做一做 】
2.如图,在△ABC中,∠B=90°,BC=10,∠BAC的角平分线AD交BC于点D,BD:DC=2:3,则点D到AC的距离是________.
【做一做 】
3.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB,交AB于点E,交AC于点F,若S△ABC=7,DE=2,AB=4,则AC=_____.
【做一做 】
4.在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB的垂直平分线分别交AC、AB于D、E两点.且DE=1cm,BD=2cm.则AC的长为_________cm.
【做一做 】
已知∠AOB和C、D两点,请在图中标出一点E,使得点E到OA、OB的距离相等,而且E点到C、D的距离也相等。
O
B
A
C
D
·
·
E
做一做
思考:已知:在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、AC上,且DE=DF.试判断∠BED与∠BFD的关系,并说明理由.
F
B
A
C
D
E
M
N
已知:在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、AC上,且DE=DF.试判断∠BED与∠BFD的关系,并说明理由.
变式:
F
B
A
C
D
M
N
E
说说你本节课你有什么收获?
【课堂小结 】
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
