2.1.2两直线平行与垂直的判定 课件(共25张PPT)
文档属性
| 名称 | 2.1.2两直线平行与垂直的判定 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 10:18:56 | ||
图片预览



文档简介
(共25张PPT)
2.1.2两直线平行和垂直的判定
人教A(2019)版
选择性必修一
1、直线的倾斜角定义:
3、直线的斜率定义:
4、过两点的直线的斜率公式:
2、倾斜角范围:
5、直线的斜率取值范围:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角。
新知导入
6、如果直线l的斜率k,则这条直线的方向向量(1,k)
复习巩固
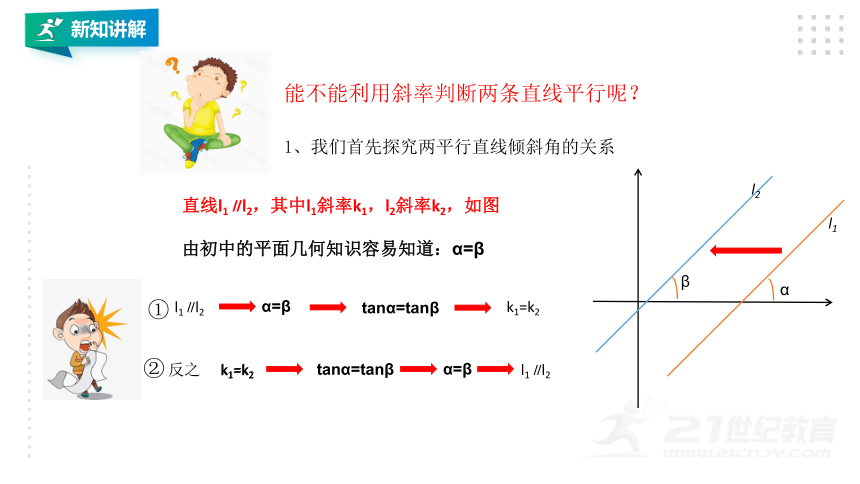
能不能利用斜率判断两条直线平行呢?
1、我们首先探究两平行直线倾斜角的关系
α
β
l1
l2
由初中的平面几何知识容易知道:α=β
直线l1∥l2,其中l1斜率k1,l2斜率k2,如图
α=β
tanα=tanβ
k1=k2
l1∥l2
反之
k1=k2
k1=k2
tanα=tanβ
α=β
l1∥l2
①
②
新知讲解
新知讲解
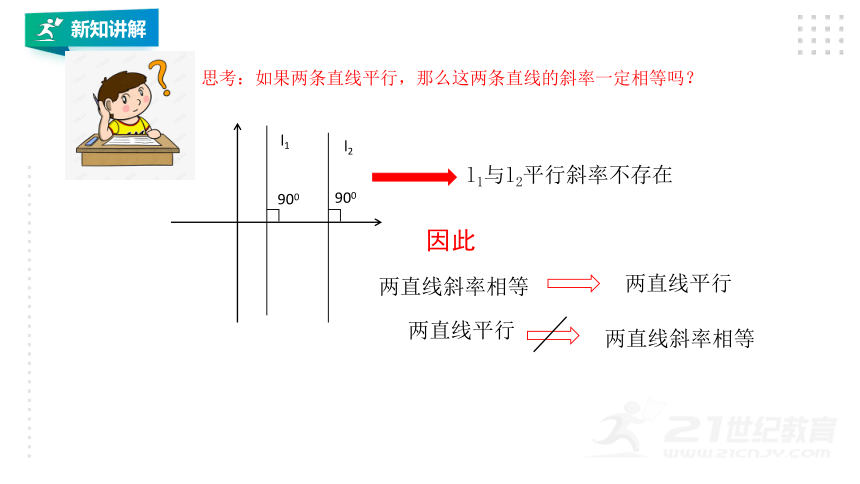
思考:如果两条直线平行,那么这两条直线的斜率一定相等吗?
∟
∟
900
900
l1
l2
l1与l2平行斜率不存在
两直线斜率相等
两直线平行
因此
两直线平行
两直线斜率相等
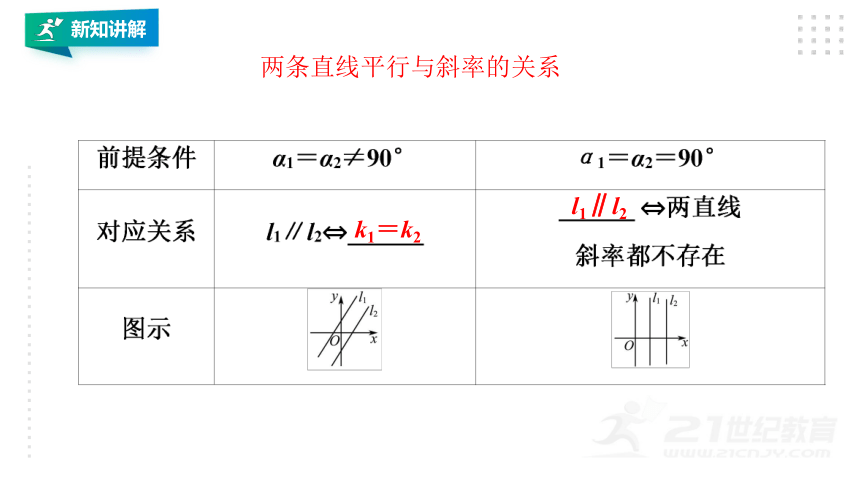
两条直线平行与斜率的关系
k1=k2
l1∥l2
新知讲解
新知讲解
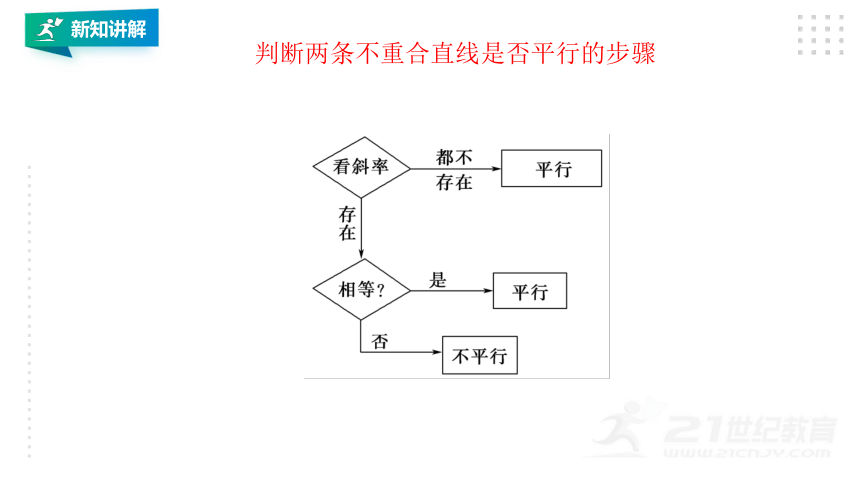
判断两条不重合直线是否平行的步骤
合作探究
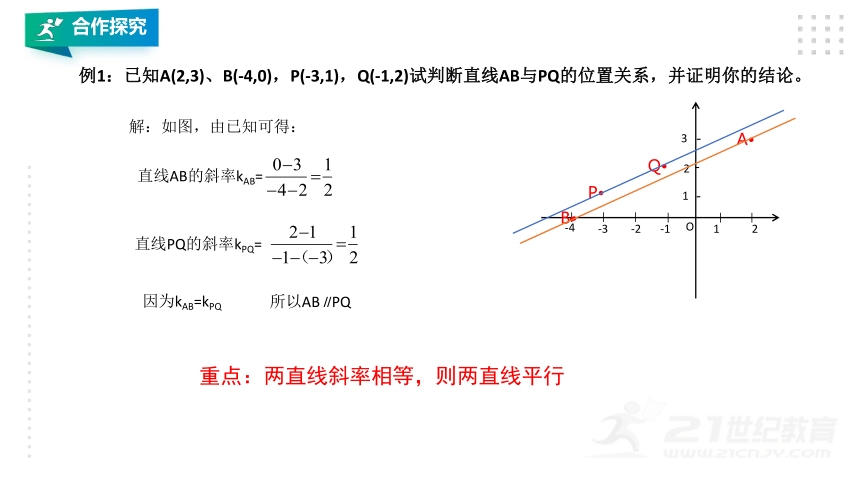
例1:已知A(2,3)、B(-4,0),P(-3,1),Q(-1,2)试判断直线AB与PQ的位置关系,并证明你的结论。
解:如图,由已知可得:
│
│
│
│
│
│
-
-
-
O
-1
-2
-3
-4
1
2
1
2
3
B
A
P
Q
直线AB的斜率kAB=
直线PQ的斜率kPQ=
因为kAB=kPQ
所以AB∥PQ
重点:两直线斜率相等,则两直线平行
合作探究
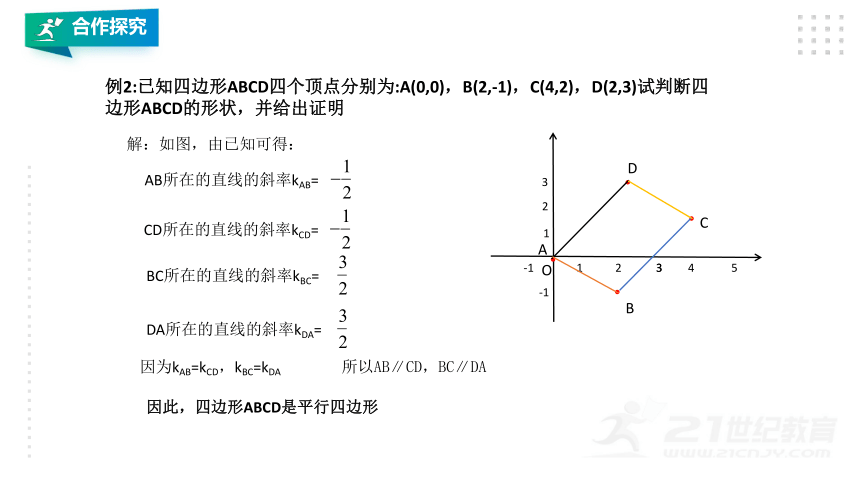
例2:已知四边形ABCD四个顶点分别为:A(0,0),B(2,-1),C(4,2),D(2,3)试判断四边形ABCD的形状,并给出证明
解:如图,由已知可得:
-1
1
2
3
4
5
-1
1
2
3
3
A
O
B
C
D
AB所在的直线的斜率kAB=
CD所在的直线的斜率kCD=
BC所在的直线的斜率kBC=
DA所在的直线的斜率kDA=
因为kAB=kCD,kBC=kDA
所以AB∥CD,BC∥DA
因此,四边形ABCD是平行四边形
1.已知过A(-2,m)和B(m,4)两点的直线与斜率为-2的直线平行,
则m的值为( )
-8
2.已知直线l1的倾斜角为45°,直线l1∥l2,且l2过点A(-2,-1)
和B(3,a),则a的值为________
4
课堂练习
新知讲解
下面我们探讨两直线垂直与两直线斜率的关系
设直线l1与l2的斜率分别为k1、k2,如图:
由上节课我们知道,l1和l2的方向向量分别为
l1 l2
1×1+k1k2=0
k1k2=-1
我们得到:当两直线斜率存在时,两直线垂直的条件:
l1 l2
k1k2=-1
反之也成立,即:
k1k2=-1
l1 l2
当两条相互的直线其中一条倾斜角900斜率不存在时,另一条
直线的倾斜角为00,斜率为0,反之亦然。
O
x
y
O
y
O
x
新知讲解
两条直线垂直与斜率的关系
k1k2=-1
垂直
新知讲解
例3、已知A(-6,0),B(3,6),P(0,3),Q(-6,6),试判断AB、PQ的位置关系。
直线AB的斜率kAB=
直线PQ的斜率kPQ=
kABkPQ=
×
=-1
解:
所以直线AB PQ
A(-6,0)
B(3,6)
P(0,3)
Q(-6,6)
例4、已知A(5,-1),B(1,1),C(2,3)三点,试判断ΔABC的形状。
解:
边AB所在的直线的斜率kAB=
边BC所在的直线的斜率kBC= 2
由kABkBC=-1,得AB BC,即∠ABC=900
所以ΔABC是直角三角形。
A(5,-1)
B(1,1)
B(2,3)
新知讲解
解:由斜率公式可得
由kBC=0, 所以BC边上的高线与x轴垂直,其斜率不存在.
例5、已知△ABC三个顶点坐标分别为A(-2,-4),B(6,6),C(0,6),求此三
角形三边的高所在直线的斜率.
A
B
C
∟
∟
∟
O
x
y
课堂练习
1、△ABC的顶点A(5,-1),B(1,1),C(2,m),若△ABC是以点A为直角
顶点的直角三角形,求m的值.
解:因为直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
2、已知直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直.
3、已知直线l1经过点A(3,a),B(a-1,2),直线l2经过点C(1,2),D(-2,a+2).
(1)若l1∥l2,求a的值;
(2)若l1⊥l2,求a的值.
课堂练习
解得a=1或a=6.
经检验,当a=1或a=6时,l1∥l2.
解:设直线l1的斜率为k1,直线l2的斜率为k2,
课堂练习
(2)若l1⊥l2.
②当k2≠0时,l2的斜率存在,
可得a=3或a=-4,
所以当a=3或a=-4时,l1⊥l2.
课堂练习
4、已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,
求点D的坐标.
解:设所求点D的坐标为(x,y),如图.
因为kAB=3,kBC=0,
所以kAB·kBC≠-1,即AB与BC不垂直.
所以AB,BC都不可作为直角梯形的直角腰.
①若CD是直角梯形的直角腰,
则BC⊥CD,AD⊥CD.
因为kBC=0,
所以CD的斜率不存在,所以x=3.
所以y=3.
此时AB与CD不平行,故所求点D的坐标为(3,3).
课堂练习
②若AD是直角梯形的直角腰,
则AD⊥AB,AD⊥CD.
课堂练习
课堂练习
5.已知A(2,3),B(1,-1),C(-1,-2),点D在x轴上,则当点D坐标
为________时,AB⊥CD.
(-9,0)
由AB⊥CD知,kAB·kCD=-1,
课堂总结
两直线平行或垂直的判定方法
斜率均不存在
平行或重合
一条直线的斜率为0,另一条直线的斜率不存在
垂直
斜率均存在
相等
积为-1
平行或重合
垂直
板书设计
不重合的两直线的位置关系
平行
垂直
两直线斜率相等
两直线平行
两直线平行
两直线斜率相等
k1=k2
l1∥l2
k1k2=-1
l1 l2
k1k2=-1
l1 l2
两直线斜率存在时:
作业布置
1.已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2).如
果l1⊥l2,求a的值.
2.已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,求
m的值.
3.课本P582、3、7、9
https://www.21cnjy.com/help/help_extract.php
2.1.2两直线平行和垂直的判定
人教A(2019)版
选择性必修一
1、直线的倾斜角定义:
3、直线的斜率定义:
4、过两点的直线的斜率公式:
2、倾斜角范围:
5、直线的斜率取值范围:
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线的倾斜角。
新知导入
6、如果直线l的斜率k,则这条直线的方向向量(1,k)
复习巩固
能不能利用斜率判断两条直线平行呢?
1、我们首先探究两平行直线倾斜角的关系
α
β
l1
l2
由初中的平面几何知识容易知道:α=β
直线l1∥l2,其中l1斜率k1,l2斜率k2,如图
α=β
tanα=tanβ
k1=k2
l1∥l2
反之
k1=k2
k1=k2
tanα=tanβ
α=β
l1∥l2
①
②
新知讲解
新知讲解
思考:如果两条直线平行,那么这两条直线的斜率一定相等吗?
∟
∟
900
900
l1
l2
l1与l2平行斜率不存在
两直线斜率相等
两直线平行
因此
两直线平行
两直线斜率相等
两条直线平行与斜率的关系
k1=k2
l1∥l2
新知讲解
新知讲解
判断两条不重合直线是否平行的步骤
合作探究
例1:已知A(2,3)、B(-4,0),P(-3,1),Q(-1,2)试判断直线AB与PQ的位置关系,并证明你的结论。
解:如图,由已知可得:
│
│
│
│
│
│
-
-
-
O
-1
-2
-3
-4
1
2
1
2
3
B
A
P
Q
直线AB的斜率kAB=
直线PQ的斜率kPQ=
因为kAB=kPQ
所以AB∥PQ
重点:两直线斜率相等,则两直线平行
合作探究
例2:已知四边形ABCD四个顶点分别为:A(0,0),B(2,-1),C(4,2),D(2,3)试判断四边形ABCD的形状,并给出证明
解:如图,由已知可得:
-1
1
2
3
4
5
-1
1
2
3
3
A
O
B
C
D
AB所在的直线的斜率kAB=
CD所在的直线的斜率kCD=
BC所在的直线的斜率kBC=
DA所在的直线的斜率kDA=
因为kAB=kCD,kBC=kDA
所以AB∥CD,BC∥DA
因此,四边形ABCD是平行四边形
1.已知过A(-2,m)和B(m,4)两点的直线与斜率为-2的直线平行,
则m的值为( )
-8
2.已知直线l1的倾斜角为45°,直线l1∥l2,且l2过点A(-2,-1)
和B(3,a),则a的值为________
4
课堂练习
新知讲解
下面我们探讨两直线垂直与两直线斜率的关系
设直线l1与l2的斜率分别为k1、k2,如图:
由上节课我们知道,l1和l2的方向向量分别为
l1 l2
1×1+k1k2=0
k1k2=-1
我们得到:当两直线斜率存在时,两直线垂直的条件:
l1 l2
k1k2=-1
反之也成立,即:
k1k2=-1
l1 l2
当两条相互的直线其中一条倾斜角900斜率不存在时,另一条
直线的倾斜角为00,斜率为0,反之亦然。
O
x
y
O
y
O
x
新知讲解
两条直线垂直与斜率的关系
k1k2=-1
垂直
新知讲解
例3、已知A(-6,0),B(3,6),P(0,3),Q(-6,6),试判断AB、PQ的位置关系。
直线AB的斜率kAB=
直线PQ的斜率kPQ=
kABkPQ=
×
=-1
解:
所以直线AB PQ
A(-6,0)
B(3,6)
P(0,3)
Q(-6,6)
例4、已知A(5,-1),B(1,1),C(2,3)三点,试判断ΔABC的形状。
解:
边AB所在的直线的斜率kAB=
边BC所在的直线的斜率kBC= 2
由kABkBC=-1,得AB BC,即∠ABC=900
所以ΔABC是直角三角形。
A(5,-1)
B(1,1)
B(2,3)
新知讲解
解:由斜率公式可得
由kBC=0, 所以BC边上的高线与x轴垂直,其斜率不存在.
例5、已知△ABC三个顶点坐标分别为A(-2,-4),B(6,6),C(0,6),求此三
角形三边的高所在直线的斜率.
A
B
C
∟
∟
∟
O
x
y
课堂练习
1、△ABC的顶点A(5,-1),B(1,1),C(2,m),若△ABC是以点A为直角
顶点的直角三角形,求m的值.
解:因为直线l1的斜率不存在,直线l2的斜率为0,所以l1⊥l2.
2、已知直线l1经过点A(3,2),B(3,-1),直线l2经过点M(1,1),N(2,1),判断l1与l2是否垂直.
3、已知直线l1经过点A(3,a),B(a-1,2),直线l2经过点C(1,2),D(-2,a+2).
(1)若l1∥l2,求a的值;
(2)若l1⊥l2,求a的值.
课堂练习
解得a=1或a=6.
经检验,当a=1或a=6时,l1∥l2.
解:设直线l1的斜率为k1,直线l2的斜率为k2,
课堂练习
(2)若l1⊥l2.
②当k2≠0时,l2的斜率存在,
可得a=3或a=-4,
所以当a=3或a=-4时,l1⊥l2.
课堂练习
4、已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,
求点D的坐标.
解:设所求点D的坐标为(x,y),如图.
因为kAB=3,kBC=0,
所以kAB·kBC≠-1,即AB与BC不垂直.
所以AB,BC都不可作为直角梯形的直角腰.
①若CD是直角梯形的直角腰,
则BC⊥CD,AD⊥CD.
因为kBC=0,
所以CD的斜率不存在,所以x=3.
所以y=3.
此时AB与CD不平行,故所求点D的坐标为(3,3).
课堂练习
②若AD是直角梯形的直角腰,
则AD⊥AB,AD⊥CD.
课堂练习
课堂练习
5.已知A(2,3),B(1,-1),C(-1,-2),点D在x轴上,则当点D坐标
为________时,AB⊥CD.
(-9,0)
由AB⊥CD知,kAB·kCD=-1,
课堂总结
两直线平行或垂直的判定方法
斜率均不存在
平行或重合
一条直线的斜率为0,另一条直线的斜率不存在
垂直
斜率均存在
相等
积为-1
平行或重合
垂直
板书设计
不重合的两直线的位置关系
平行
垂直
两直线斜率相等
两直线平行
两直线平行
两直线斜率相等
k1=k2
l1∥l2
k1k2=-1
l1 l2
k1k2=-1
l1 l2
两直线斜率存在时:
作业布置
1.已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2).如
果l1⊥l2,求a的值.
2.已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,求
m的值.
3.课本P582、3、7、9
https://www.21cnjy.com/help/help_extract.php
