4.1.1 正弦的概念与30°角的正弦值 同步练习(含答案)
文档属性
| 名称 | 4.1.1 正弦的概念与30°角的正弦值 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 12:55:06 | ||
图片预览

文档简介
4.1 正弦和余弦
第1课时 正弦的概念与30°角的正弦值
一、选择题
1.【中考·怀化】已知∠α为锐角,且sinα=,则∠α=( )
A.30° B.45° C.60° D.90°
2.【2021·滁州定远县期末】在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA等于( )
A. B. C. D.
3.【中考·乐山】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB= B.sinB= C.sinB= D.sinB=
第3题图 第9题图 第11题图 第12题图
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a=3,b=4,则sinA+sinB的值为( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,AB=3BC.则sinA的值是( )
A. 3 B. C. D.
6.在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
7.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
8.Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( )
A.5 B.4.8 C.4.6 D.4
9.【2020·雅安】如图,在△ACB中,∠C=90°,sinB=,若AC=6,则BC的长为( )
A.8 B.12 C.6 D.12
10.在Rt△ABC中,∠C=90°,若将各边长度都扩大到原来的2倍,则锐角A的正弦值( )
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.无法确定
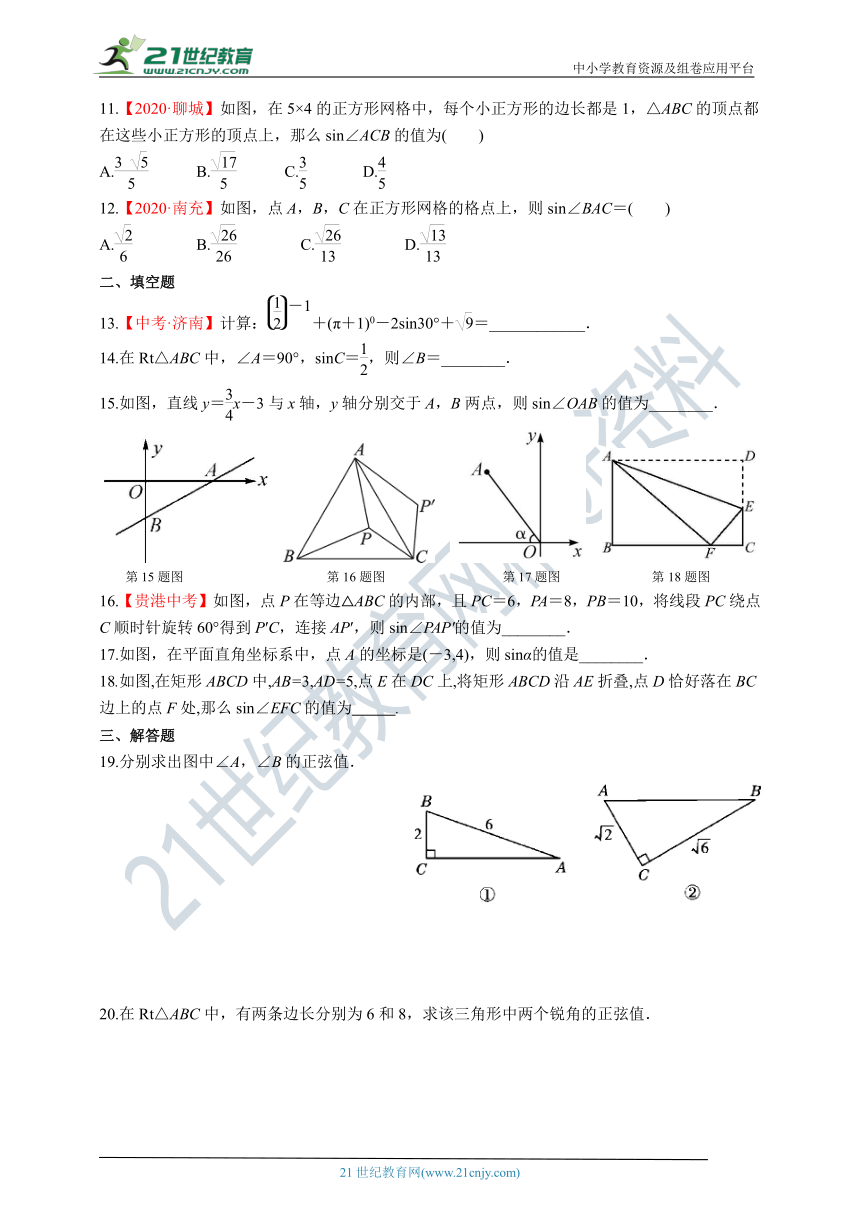
11.【2020·聊城】如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
12.【2020·南充】如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A. B. C. D.
二、填空题
13.【中考·济南】计算:+(π+1)0-2sin30°+=____________.
14.在Rt△ABC中,∠A=90°,sinC=,则∠B=________.
15.如图,直线y=x-3与x轴,y轴分别交于A,B两点,则sin∠OAB的值为________.
第15题图 第16题图 第17题图 第18题图
16.【贵港中考】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P′C,连接AP′,则sin∠PAP'的值为________.
17.如图,在平面直角坐标系中,点A的坐标是(-3,4),则sinα的值是________.
18.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
三、解答题
19.分别求出图中∠A,∠B的正弦值.
20.在Rt△ABC中,有两条边长分别为6和8,求该三角形中两个锐角的正弦值.
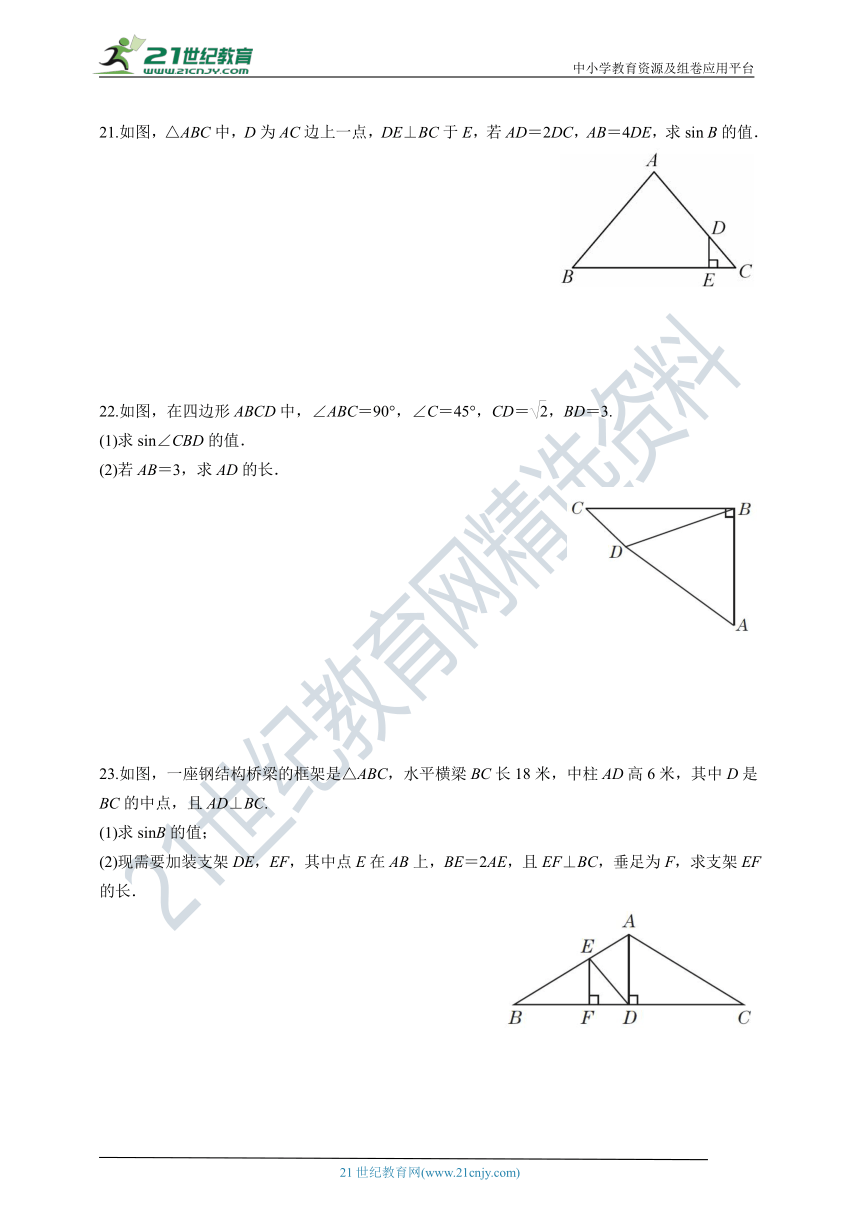
21.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,求sin B的值.
22.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值.
(2)若AB=3,求AD的长.
23.如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为F,求支架EF的长.
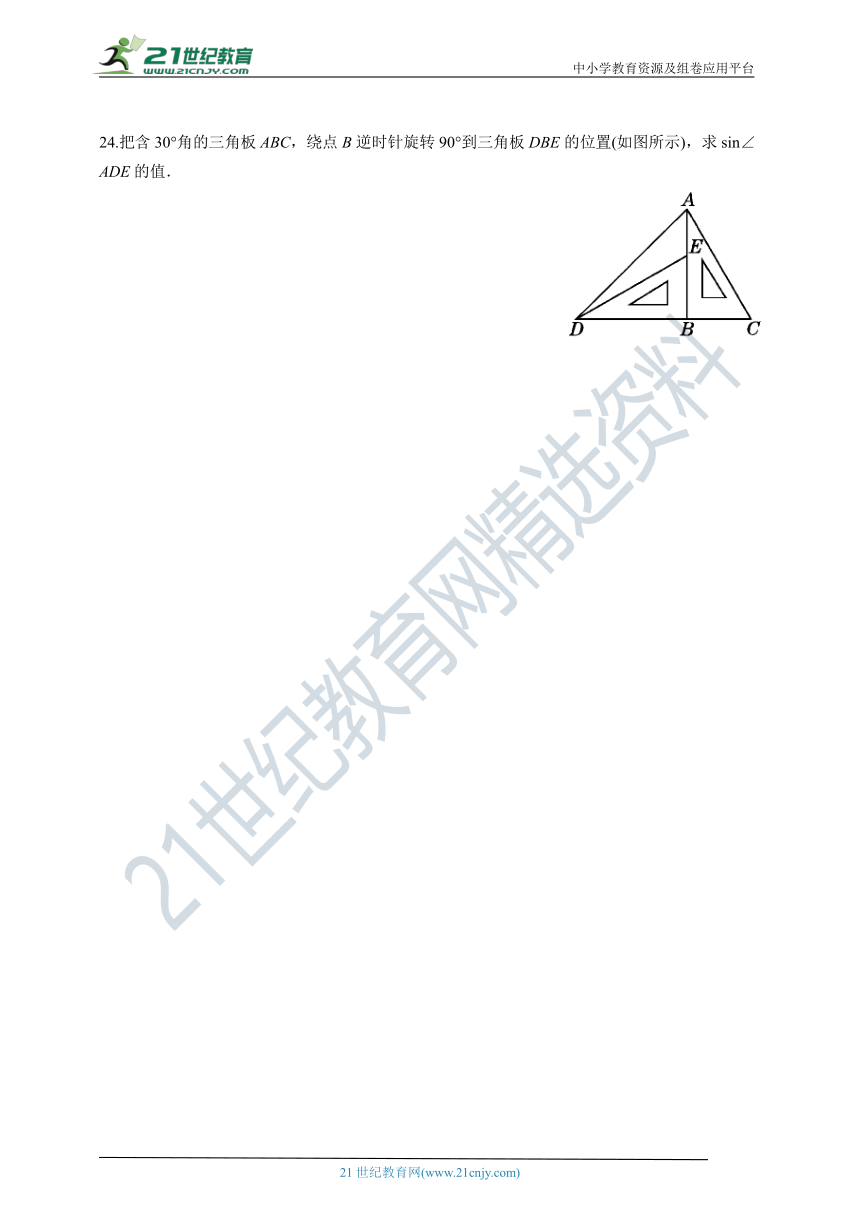
24.把含30°角的三角板ABC,绕点B逆时针旋转90°到三角板DBE的位置(如图所示),求sin∠ADE的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
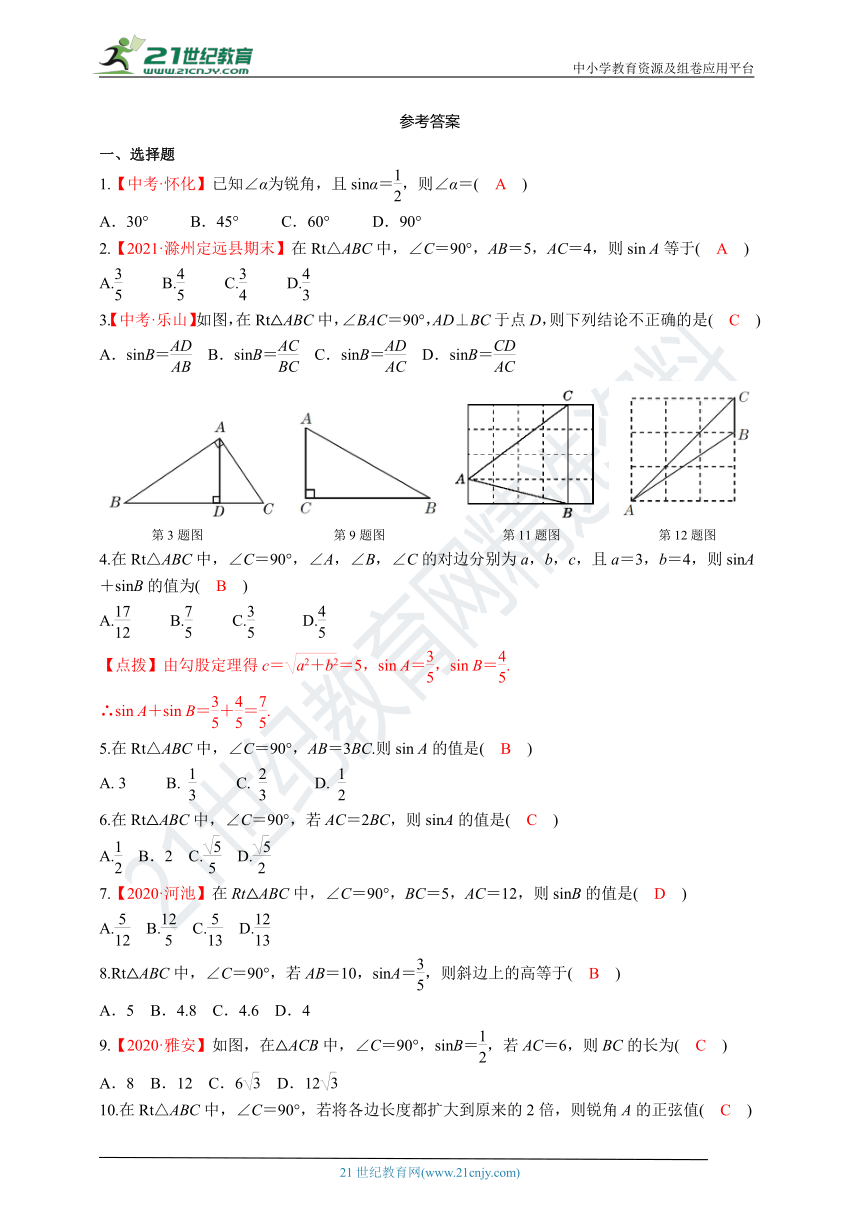
1.【中考·怀化】已知∠α为锐角,且sinα=,则∠α=( A )
A.30° B.45° C.60° D.90°
2.【2021·滁州定远县期末】在Rt△ABC中,∠C=90°,AB=5,AC=4,则sin A等于( A )
A. B. C. D.
3.【中考·乐山】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( C )
A.sinB= B.sinB= C.sinB= D.sinB=
第3题图 第9题图 第11题图 第12题图
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a=3,b=4,则sinA+sinB的值为( B )
A. B. C. D.
【点拨】由勾股定理得c==5,sin A=,sin B=.
∴sin A+sin B=+=.
5.在Rt△ABC中,∠C=90°,AB=3BC.则sin A的值是( B )
A. 3 B. C. D.
6.在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( C )
A. B.2 C. D.
7.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( D )
A. B. C. D.
8.Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( B )
A.5 B.4.8 C.4.6 D.4
9.【2020·雅安】如图,在△ACB中,∠C=90°,sinB=,若AC=6,则BC的长为( C )
A.8 B.12 C.6 D.12
10.在Rt△ABC中,∠C=90°,若将各边长度都扩大到原来的2倍,则锐角A的正弦值( C )
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.无法确定
11.【2020·聊城】如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( D )
A. B. C. D.
12.【2020·南充】如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( B )
A. B. C. D.
【点拨】如图,作BD⊥AC于D,设正方形网格的边长为1,由勾股定理得,AB==,
AC==3,
∵S△ABC=AC·BD=×3·BD=×1×3,
∴BD=,∴sin∠BAC===.
二、填空题
13.【中考·济南】计算:+(π+1)0-2sin30°+=____________.
【点拨】原式=2+1-2×+3=3-1+3=5.
14.在Rt△ABC中,∠A=90°,sinC=,则∠B=________.
【答案】60°
15.如图,直线y=x-3与x轴,y轴分别交于A,B两点,则sin∠OAB的值为________.
【答案】
第15题图 第16题图 第17题图 第18题图
16.【贵港中考】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P′C,连接AP′,则sin∠PAP'的值为________.
【答案】
17.如图,在平面直角坐标系中,点A的坐标是(-3,4),则sinα的值是________.
【答案】
18.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
【答案】
三、解答题
19.分别求出图中∠A,∠B的正弦值.
解:图①:AC===4 ,
∴sinA==,sin B==.
图②:AB===2 ,
∴sinA===,sinB===.
20.在Rt△ABC中,有两条边长分别为6和8,求该三角形中两个锐角的正弦值.
【点拨】因为6,8,10为一组勾股数,易因默认斜边长为10而出错,题中并未说明6,8均为直角边长.
解:当6,8都是直角边长时,两个锐角的正弦值分别为,;当斜边长是8时,由勾股定理得另一条直角边长是2,两个锐角的正弦值分别为,.
21.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,求sin B的值.
解:过点A作AF⊥BC于F,AD=2DC,AC=AD+CD=2DC+CD=3CD.
∵AF⊥BC,DE⊥BC,
∴DE∥AF,∴===.
设DE=a,则AF=3a,AB=4a,
∴sin B===.
22.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值.
解:如图,过点D作DE⊥BC于点E,
在Rt△CED中,
∵∠C=45°,CD=,∴CE=DE=1.
在Rt△BDE中,sin∠CBD==.
(2)若AB=3,求AD的长.
解:如图,过点D作DF⊥AB于点F,则∠BFD=∠BED=∠ABC=90°.
∴四边形BEDF为矩形.∴DE=BF=1.
∵BD=3,∴DF=2.
∴AF=AB-BF=2.∴AD=2.
23.如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
解:在Rt△ABD中,∵BD=BC=9米,AD=6米,
∴AB===3(米),
∴sin B===.
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为F,求支架EF的长.
解:在△BEF中,∵sin B=,
∴EF=BE·sin B.
又∵BE=2AE,∴BE=AB.
∴EF=·AB·sin B=4(米)
即支架EF的长为4米.
24.把含30°角的三角板ABC,绕点B逆时针旋转90°到三角板DBE的位置(如图所示),求sin∠ADE的值.
解:如图,过点E作EF⊥AD,交AD于点F.
设BD=x,则AB=x,BE=x,DE=x.
由勾股定理,得AD=x,易证△ABD∽△AFE,
∴==,即=,
∴EF=x.
在Rt△DEF中,根据三角函数的定义可得
sin∠ADE==.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1课时 正弦的概念与30°角的正弦值
一、选择题
1.【中考·怀化】已知∠α为锐角,且sinα=,则∠α=( )
A.30° B.45° C.60° D.90°
2.【2021·滁州定远县期末】在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA等于( )
A. B. C. D.
3.【中考·乐山】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB= B.sinB= C.sinB= D.sinB=
第3题图 第9题图 第11题图 第12题图
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a=3,b=4,则sinA+sinB的值为( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,AB=3BC.则sinA的值是( )
A. 3 B. C. D.
6.在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )
A. B.2 C. D.
7.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
8.Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( )
A.5 B.4.8 C.4.6 D.4
9.【2020·雅安】如图,在△ACB中,∠C=90°,sinB=,若AC=6,则BC的长为( )
A.8 B.12 C.6 D.12
10.在Rt△ABC中,∠C=90°,若将各边长度都扩大到原来的2倍,则锐角A的正弦值( )
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.无法确定
11.【2020·聊城】如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
12.【2020·南充】如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A. B. C. D.
二、填空题
13.【中考·济南】计算:+(π+1)0-2sin30°+=____________.
14.在Rt△ABC中,∠A=90°,sinC=,则∠B=________.
15.如图,直线y=x-3与x轴,y轴分别交于A,B两点,则sin∠OAB的值为________.
第15题图 第16题图 第17题图 第18题图
16.【贵港中考】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P′C,连接AP′,则sin∠PAP'的值为________.
17.如图,在平面直角坐标系中,点A的坐标是(-3,4),则sinα的值是________.
18.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
三、解答题
19.分别求出图中∠A,∠B的正弦值.
20.在Rt△ABC中,有两条边长分别为6和8,求该三角形中两个锐角的正弦值.
21.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,求sin B的值.
22.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值.
(2)若AB=3,求AD的长.
23.如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为F,求支架EF的长.
24.把含30°角的三角板ABC,绕点B逆时针旋转90°到三角板DBE的位置(如图所示),求sin∠ADE的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·怀化】已知∠α为锐角,且sinα=,则∠α=( A )
A.30° B.45° C.60° D.90°
2.【2021·滁州定远县期末】在Rt△ABC中,∠C=90°,AB=5,AC=4,则sin A等于( A )
A. B. C. D.
3.【中考·乐山】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( C )
A.sinB= B.sinB= C.sinB= D.sinB=
第3题图 第9题图 第11题图 第12题图
4.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a=3,b=4,则sinA+sinB的值为( B )
A. B. C. D.
【点拨】由勾股定理得c==5,sin A=,sin B=.
∴sin A+sin B=+=.
5.在Rt△ABC中,∠C=90°,AB=3BC.则sin A的值是( B )
A. 3 B. C. D.
6.在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( C )
A. B.2 C. D.
7.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( D )
A. B. C. D.
8.Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( B )
A.5 B.4.8 C.4.6 D.4
9.【2020·雅安】如图,在△ACB中,∠C=90°,sinB=,若AC=6,则BC的长为( C )
A.8 B.12 C.6 D.12
10.在Rt△ABC中,∠C=90°,若将各边长度都扩大到原来的2倍,则锐角A的正弦值( C )
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.无法确定
11.【2020·聊城】如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( D )
A. B. C. D.
12.【2020·南充】如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( B )
A. B. C. D.
【点拨】如图,作BD⊥AC于D,设正方形网格的边长为1,由勾股定理得,AB==,
AC==3,
∵S△ABC=AC·BD=×3·BD=×1×3,
∴BD=,∴sin∠BAC===.
二、填空题
13.【中考·济南】计算:+(π+1)0-2sin30°+=____________.
【点拨】原式=2+1-2×+3=3-1+3=5.
14.在Rt△ABC中,∠A=90°,sinC=,则∠B=________.
【答案】60°
15.如图,直线y=x-3与x轴,y轴分别交于A,B两点,则sin∠OAB的值为________.
【答案】
第15题图 第16题图 第17题图 第18题图
16.【贵港中考】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P′C,连接AP′,则sin∠PAP'的值为________.
【答案】
17.如图,在平面直角坐标系中,点A的坐标是(-3,4),则sinα的值是________.
【答案】
18.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
【答案】
三、解答题
19.分别求出图中∠A,∠B的正弦值.
解:图①:AC===4 ,
∴sinA==,sin B==.
图②:AB===2 ,
∴sinA===,sinB===.
20.在Rt△ABC中,有两条边长分别为6和8,求该三角形中两个锐角的正弦值.
【点拨】因为6,8,10为一组勾股数,易因默认斜边长为10而出错,题中并未说明6,8均为直角边长.
解:当6,8都是直角边长时,两个锐角的正弦值分别为,;当斜边长是8时,由勾股定理得另一条直角边长是2,两个锐角的正弦值分别为,.
21.如图,△ABC中,D为AC边上一点,DE⊥BC于E,若AD=2DC,AB=4DE,求sin B的值.
解:过点A作AF⊥BC于F,AD=2DC,AC=AD+CD=2DC+CD=3CD.
∵AF⊥BC,DE⊥BC,
∴DE∥AF,∴===.
设DE=a,则AF=3a,AB=4a,
∴sin B===.
22.如图,在四边形ABCD中,∠ABC=90°,∠C=45°,CD=,BD=3.
(1)求sin∠CBD的值.
解:如图,过点D作DE⊥BC于点E,
在Rt△CED中,
∵∠C=45°,CD=,∴CE=DE=1.
在Rt△BDE中,sin∠CBD==.
(2)若AB=3,求AD的长.
解:如图,过点D作DF⊥AB于点F,则∠BFD=∠BED=∠ABC=90°.
∴四边形BEDF为矩形.∴DE=BF=1.
∵BD=3,∴DF=2.
∴AF=AB-BF=2.∴AD=2.
23.如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
解:在Rt△ABD中,∵BD=BC=9米,AD=6米,
∴AB===3(米),
∴sin B===.
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为F,求支架EF的长.
解:在△BEF中,∵sin B=,
∴EF=BE·sin B.
又∵BE=2AE,∴BE=AB.
∴EF=·AB·sin B=4(米)
即支架EF的长为4米.
24.把含30°角的三角板ABC,绕点B逆时针旋转90°到三角板DBE的位置(如图所示),求sin∠ADE的值.
解:如图,过点E作EF⊥AD,交AD于点F.
设BD=x,则AB=x,BE=x,DE=x.
由勾股定理,得AD=x,易证△ABD∽△AFE,
∴==,即=,
∴EF=x.
在Rt△DEF中,根据三角函数的定义可得
sin∠ADE==.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
