4.1.3 余弦与特殊角的余弦值 同步练习(含解析)
文档属性
| 名称 | 4.1.3 余弦与特殊角的余弦值 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 08:17:22 | ||
图片预览




文档简介
4.1 正弦和余弦
第3课时 余弦与特殊角的余弦值
一、选择题
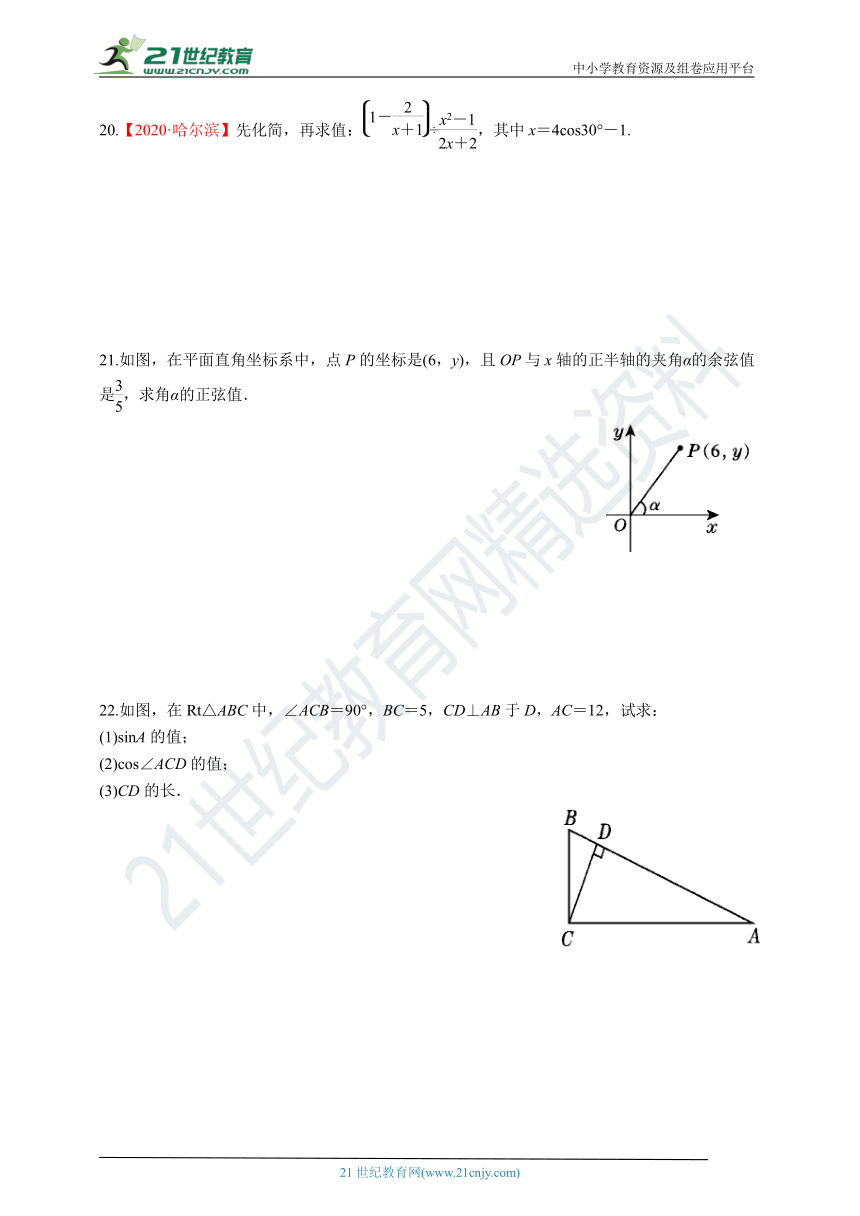
1.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,下列不能表示cos A的是( )
A. B. C. D.
第1题图 第2题图 第3题图 第5题图
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
3.如图所示,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,BC=10,cos∠DCA=,则AB的值是 ( )
A.9 B.8 C.6 D.3
4.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
5.【中考·湖州】如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B. C. D.
6.【2020·柳州】如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB=( )
A. B. C. D.
第6题图 第7题图 第12题图
7.在Rt△ABC中,∠C=90°,若AB=2AC,则cosA的值是( )
A. B. C. D.
8.【中考·广东】如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( )
A. B. C. D.
10.已知α,β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A.α=β B.α+β=90° C.α-β=90° D.β-α=90°
11.已知锐角三角形ABC中,|2cosA-1|+(1-2cos2B)2=0,则∠C=( )
A.30° B.45° C.60° D.75°
12.【2020·安徽】如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为( )
A. B. C. D.4
二、填空题
13.cos30°=______________,cos45°=____________,cos60°=____________.
14.【中考·绵阳改编】在△ABC中,若∠B=45°,AB=10,AC=5,则BC的长是________.
15.【中考·白色】计算:+-(3-π)0-=________.
16.【中考·贵港】计算:+(+π)0--2cos60°=________.
17.【中考·杭州】在直角三角形ABC中,若2AB=AC,则cosC=____________.
18.如图,已知每个小正方形的边长为1,点A,B,C是小正方形的顶点,则cos∠BAC的值为______.
三、解答题
19.计算.
(1)【2020·岳阳】+2cos60°-(4-π)0+|-|;
(2)2cos245°+cos260°-3cos230°+2sin30°.
(3)【2021·张家界】
(4)【2021·泸州】计算:.
(5)2sin30°+cos60°-cos245°;
(6)-sin60°(1-sin30°).
20.【2020·哈尔滨】先化简,再求值:÷,其中x=4cos30°-1.
21.如图,在平面直角坐标系中,点P的坐标是(6,y),且OP与x轴的正半轴的夹角α的余弦值是,求角α的正弦值.
22.如图,在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB于D,AC=12,试求:
(1)sinA的值;
(2)cos∠ACD的值;
(3)CD的长.
23.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;(2)cos∠BAO的值.
24.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的余弦值的变化规律;
(2)根据你探索到的规律,试比较19°,36°,52°,65°,85°这些锐角的余弦值的大小;
(3)比较大小.(填“>”“<”或“=”)
若∠α=45°,则sinα________cosα;
若∠α<45°,则sinα________cosα;
若∠α>45°,则sinα________cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小.
sin10°,cos30°,sin50°,cos70°.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,下列不能表示cos A的是( C )
A. B. C. D.
【点拨】∵∠A+∠ABD=90°,∠CBD+∠ABD=90°,∴∠A=∠CBD,∴cos A=cos∠CBD===.
第1题图 第2题图 第3题图 第5题图
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( C )
A. B. C. D.
3.如图所示,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,BC=10,cos∠DCA=,则AB的值是 ( C )
A.9 B.8 C.6 D.3
4.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( C )
A. B. C.或 D.或
5.【中考·湖州】如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cos B的值是( A )
A. B. C. D.
6.【2020·柳州】如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB=( C )
A. B. C. D.
第6题图 第7题图 第12题图
7.在Rt△ABC中,∠C=90°,若AB=2AC,则cosA的值是( B )
A. B. C. D.
8.【中考·广东】如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( D )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( A )
A. B. C. D.
【点拨】在Rt△ABC中,若∠C=90°,则cosB=sinA.
10.已知α,β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( B )
A.α=β B.α+β=90° C.α-β=90° D.β-α=90°
11.已知锐角三角形ABC中,|2cosA-1|+(1-2cos2B)2=0,则∠C=( D )
A.30° B.45° C.60° D.75°
【点拨】∵在锐角三角形ABC中,|2cos A-1|+(1-2cos2B)2=0,∴cosA=,cosB=(负值已舍去),∴∠A=60°,∠B=45°,∴∠C=75°.
12.【2020·安徽】如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为( C )
A. B. C. D.4
【点拨】在Rt△ABC中,∵AC=4,cosA=,
∴AB=5,根据勾股定理得BC==3,
∵∠DBC=∠A,∠C=∠C,∴△CBD∽△CAB,∴=,即=,∴BD=.
二、填空题
13.cos30°=______________,cos45°=____________,cos60°=____________.
【答案】;;
14.【中考·绵阳改编】在△ABC中,若∠B=45°,AB=10,AC=5,则BC的长是________.
【答案】15或5
15.【中考·白色】计算:+-(3-π)0-=________.
【答案】2
16.【中考·贵港】计算:+(+π)0--2cos60°=________.
【答案】-1
17.【中考·杭州】在直角三角形ABC中,若2AB=AC,则cosC=____________.
【点拨】若∠B=90°,设AB=x,则AC=2x,所以BC==x,所以cos C==;若∠A=90°,设AB=x,则AC=2x,所以BC==x,所以cos C==.综上所述,cos C的值为或.
【答案】或
18.如图,已知每个小正方形的边长为1,点A,B,C是小正方形的顶点,则cos∠BAC的值为______.
【点拨】如图,连接BC,由勾股定理得AB=BC=,AC=,∴AB2+BC2=AC2,∴△ABC是等腰直角三角形,∴∠BAC=45°,∴cos∠BAC=.本题易错点是没有先连接BC并判断△ABC是直角三角形,而直接运用cos∠BAC=得出结论.
【答案】
三、解答题
19.计算.
(1)【2020·岳阳】+2 cos 60°-(4-π)0+|-|;
解:原式=2+2×-1+=2+1-1+=2+.
(2)2cos245°+cos260°-3cos230°+2sin30°.
原式=2×+-3×+2×=1+-+1=-1+1=0.
(3)【2021·张家界】
【答案】
【解析】
解:
.
(4)【2021·泸州】计算:.
【答案】12.
【分析】根据零指数幂,负整指数幂,去括号法则,特殊角的三角函数值化简,然后再计算即可.
解:原式=1+4+4+2×
=1+4+4+3
=12
(5)2sin 30°+cos 60°-cos245°;
解:原式=2sin 30°+cos 60°-cos245°
=2×+-
=1+-
=1.
(6)-sin 60°(1-sin 30°).
解:原式=-×=-×=.
20.【2020·哈尔滨】先化简,再求值:÷,其中x=4cos 30°-1.
解:原式=÷
=·=.
∵x=4 cos 30°-1=4×-1=2 -1,
∴原式===.
21.如图,在平面直角坐标系中,点P的坐标是(6,y),且OP与x轴的正半轴的夹角α的余弦值是,求角α的正弦值.
解:如图,过点P作PC⊥x轴于C.
∵角α的余弦值是,∴=.
又∵OC=6,
∴OP=10,根据勾股定理得PC=8.
∴sinα==.
22.如图,在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB于D,AC=12,试求:
(1)sin A的值;
解:在Rt△ABC中,由BC=5,AC=12,得AB=13,
sin A=.
(2)cos∠ACD的值;
解:∵CD⊥AB,∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴cos∠ACD=sinA=.
(3)CD的长.
∵sin A=,
∴CD=AC·sin A=12×=.
23.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;(2)cos∠BAO的值.
解:(1)作BH⊥OA,垂足为H,在Rt△OHB中,
∵BO=5,sin∠BOA=,
∴BH=3,∴OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,
∴AB=3,
∴cos∠BAO==.
24.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的余弦值的变化规律;
解:在图中,cos∠B1AC=,cos∠B2AC=,
cos∠B3AC=.
∵AB3即cos∠B1AC<cos∠B2AC<cos∠B3AC.
∴余弦值随锐角度数的增大而减小.
(2)根据你探索到的规律,试比较19°,36°,52°,65°,85°这些锐角的余弦值的大小;
解:cos85°<cos65°<cos52°<cos36°<cos19°.
(3)比较大小.(填“>”“<”或“=”)
若∠α=45°,则sinα________cosα;
若∠α<45°,则sinα________cosα;
若∠α>45°,则sinα________cosα;
【答案】= < >
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小.
sin10°,cos30°,sin50°,cos70°.
解:cos30°>sin50°>cos70°>sin10°.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3课时 余弦与特殊角的余弦值
一、选择题
1.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,下列不能表示cos A的是( )
A. B. C. D.
第1题图 第2题图 第3题图 第5题图
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
3.如图所示,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,BC=10,cos∠DCA=,则AB的值是 ( )
A.9 B.8 C.6 D.3
4.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
5.【中考·湖州】如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A. B. C. D.
6.【2020·柳州】如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB=( )
A. B. C. D.
第6题图 第7题图 第12题图
7.在Rt△ABC中,∠C=90°,若AB=2AC,则cosA的值是( )
A. B. C. D.
8.【中考·广东】如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( )
A. B. C. D.
10.已知α,β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A.α=β B.α+β=90° C.α-β=90° D.β-α=90°
11.已知锐角三角形ABC中,|2cosA-1|+(1-2cos2B)2=0,则∠C=( )
A.30° B.45° C.60° D.75°
12.【2020·安徽】如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为( )
A. B. C. D.4
二、填空题
13.cos30°=______________,cos45°=____________,cos60°=____________.
14.【中考·绵阳改编】在△ABC中,若∠B=45°,AB=10,AC=5,则BC的长是________.
15.【中考·白色】计算:+-(3-π)0-=________.
16.【中考·贵港】计算:+(+π)0--2cos60°=________.
17.【中考·杭州】在直角三角形ABC中,若2AB=AC,则cosC=____________.
18.如图,已知每个小正方形的边长为1,点A,B,C是小正方形的顶点,则cos∠BAC的值为______.
三、解答题
19.计算.
(1)【2020·岳阳】+2cos60°-(4-π)0+|-|;
(2)2cos245°+cos260°-3cos230°+2sin30°.
(3)【2021·张家界】
(4)【2021·泸州】计算:.
(5)2sin30°+cos60°-cos245°;
(6)-sin60°(1-sin30°).
20.【2020·哈尔滨】先化简,再求值:÷,其中x=4cos30°-1.
21.如图,在平面直角坐标系中,点P的坐标是(6,y),且OP与x轴的正半轴的夹角α的余弦值是,求角α的正弦值.
22.如图,在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB于D,AC=12,试求:
(1)sinA的值;
(2)cos∠ACD的值;
(3)CD的长.
23.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;(2)cos∠BAO的值.
24.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的余弦值的变化规律;
(2)根据你探索到的规律,试比较19°,36°,52°,65°,85°这些锐角的余弦值的大小;
(3)比较大小.(填“>”“<”或“=”)
若∠α=45°,则sinα________cosα;
若∠α<45°,则sinα________cosα;
若∠α>45°,则sinα________cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小.
sin10°,cos30°,sin50°,cos70°.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,下列不能表示cos A的是( C )
A. B. C. D.
【点拨】∵∠A+∠ABD=90°,∠CBD+∠ABD=90°,∴∠A=∠CBD,∴cos A=cos∠CBD===.
第1题图 第2题图 第3题图 第5题图
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( C )
A. B. C. D.
3.如图所示,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,BC=10,cos∠DCA=,则AB的值是 ( C )
A.9 B.8 C.6 D.3
4.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( C )
A. B. C.或 D.或
5.【中考·湖州】如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cos B的值是( A )
A. B. C. D.
6.【2020·柳州】如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB=( C )
A. B. C. D.
第6题图 第7题图 第12题图
7.在Rt△ABC中,∠C=90°,若AB=2AC,则cosA的值是( B )
A. B. C. D.
8.【中考·广东】如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是( D )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( A )
A. B. C. D.
【点拨】在Rt△ABC中,若∠C=90°,则cosB=sinA.
10.已知α,β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( B )
A.α=β B.α+β=90° C.α-β=90° D.β-α=90°
11.已知锐角三角形ABC中,|2cosA-1|+(1-2cos2B)2=0,则∠C=( D )
A.30° B.45° C.60° D.75°
【点拨】∵在锐角三角形ABC中,|2cos A-1|+(1-2cos2B)2=0,∴cosA=,cosB=(负值已舍去),∴∠A=60°,∠B=45°,∴∠C=75°.
12.【2020·安徽】如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为( C )
A. B. C. D.4
【点拨】在Rt△ABC中,∵AC=4,cosA=,
∴AB=5,根据勾股定理得BC==3,
∵∠DBC=∠A,∠C=∠C,∴△CBD∽△CAB,∴=,即=,∴BD=.
二、填空题
13.cos30°=______________,cos45°=____________,cos60°=____________.
【答案】;;
14.【中考·绵阳改编】在△ABC中,若∠B=45°,AB=10,AC=5,则BC的长是________.
【答案】15或5
15.【中考·白色】计算:+-(3-π)0-=________.
【答案】2
16.【中考·贵港】计算:+(+π)0--2cos60°=________.
【答案】-1
17.【中考·杭州】在直角三角形ABC中,若2AB=AC,则cosC=____________.
【点拨】若∠B=90°,设AB=x,则AC=2x,所以BC==x,所以cos C==;若∠A=90°,设AB=x,则AC=2x,所以BC==x,所以cos C==.综上所述,cos C的值为或.
【答案】或
18.如图,已知每个小正方形的边长为1,点A,B,C是小正方形的顶点,则cos∠BAC的值为______.
【点拨】如图,连接BC,由勾股定理得AB=BC=,AC=,∴AB2+BC2=AC2,∴△ABC是等腰直角三角形,∴∠BAC=45°,∴cos∠BAC=.本题易错点是没有先连接BC并判断△ABC是直角三角形,而直接运用cos∠BAC=得出结论.
【答案】
三、解答题
19.计算.
(1)【2020·岳阳】+2 cos 60°-(4-π)0+|-|;
解:原式=2+2×-1+=2+1-1+=2+.
(2)2cos245°+cos260°-3cos230°+2sin30°.
原式=2×+-3×+2×=1+-+1=-1+1=0.
(3)【2021·张家界】
【答案】
【解析】
解:
.
(4)【2021·泸州】计算:.
【答案】12.
【分析】根据零指数幂,负整指数幂,去括号法则,特殊角的三角函数值化简,然后再计算即可.
解:原式=1+4+4+2×
=1+4+4+3
=12
(5)2sin 30°+cos 60°-cos245°;
解:原式=2sin 30°+cos 60°-cos245°
=2×+-
=1+-
=1.
(6)-sin 60°(1-sin 30°).
解:原式=-×=-×=.
20.【2020·哈尔滨】先化简,再求值:÷,其中x=4cos 30°-1.
解:原式=÷
=·=.
∵x=4 cos 30°-1=4×-1=2 -1,
∴原式===.
21.如图,在平面直角坐标系中,点P的坐标是(6,y),且OP与x轴的正半轴的夹角α的余弦值是,求角α的正弦值.
解:如图,过点P作PC⊥x轴于C.
∵角α的余弦值是,∴=.
又∵OC=6,
∴OP=10,根据勾股定理得PC=8.
∴sinα==.
22.如图,在Rt△ABC中,∠ACB=90°,BC=5,CD⊥AB于D,AC=12,试求:
(1)sin A的值;
解:在Rt△ABC中,由BC=5,AC=12,得AB=13,
sin A=.
(2)cos∠ACD的值;
解:∵CD⊥AB,∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴cos∠ACD=sinA=.
(3)CD的长.
∵sin A=,
∴CD=AC·sin A=12×=.
23.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
求:(1)点B的坐标;(2)cos∠BAO的值.
解:(1)作BH⊥OA,垂足为H,在Rt△OHB中,
∵BO=5,sin∠BOA=,
∴BH=3,∴OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,
∴AB=3,
∴cos∠BAO==.
24.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的余弦值的变化规律;
解:在图中,cos∠B1AC=,cos∠B2AC=,
cos∠B3AC=.
∵AB3
∴余弦值随锐角度数的增大而减小.
(2)根据你探索到的规律,试比较19°,36°,52°,65°,85°这些锐角的余弦值的大小;
解:cos85°<cos65°<cos52°<cos36°<cos19°.
(3)比较大小.(填“>”“<”或“=”)
若∠α=45°,则sinα________cosα;
若∠α<45°,则sinα________cosα;
若∠α>45°,则sinα________cosα;
【答案】= < >
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小.
sin10°,cos30°,sin50°,cos70°.
解:cos30°>sin50°>cos70°>sin10°.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
