4.2　正切 同步练习（含解析）

4.2　正　切
一、选择题
1.【中考·黄冈】下列运算结果正确的是(　　)
A．3a3·2a2＝6a6 B．(－2a)2＝－4a2 C．tan45°＝ D．cos30°＝
2.在等腰△ABC中，∠C＝90°，则tanB＝(　　)
A. B. C. D．1
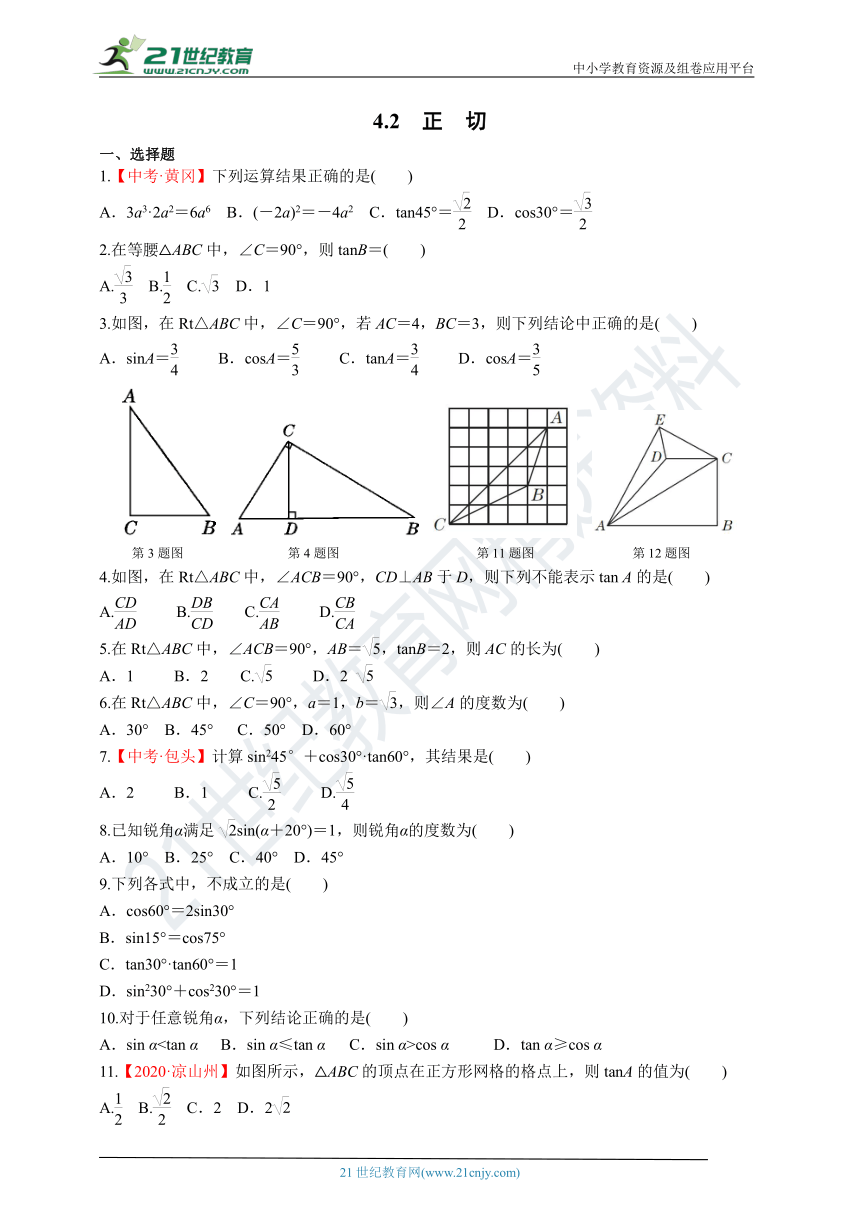
3.如图，在Rt△ABC中，∠C＝90°，若AC＝4，BC＝3，则下列结论中正确的是(　　)
A．sinA＝ B．cosA＝ C．tanA＝ D．cosA＝
第3题图 第4题图 第11题图 第12题图
4.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，则下列不能表示tan A的是(　　)
A. B. C. D.
5.在Rt△ABC中，∠ACB＝90°，AB＝，tanB＝2，则AC的长为(　　)
A．1 B．2 C. D．2
6.在Rt△ABC中，∠C＝90°，a＝1，b＝，则∠A的度数为(　　)
A．30° B．45° C．50° D．60°
7.【中考·包头】计算sin245°＋cos30°·tan60°，其结果是(　　)
A．2 B．1 C. D.
8.已知锐角α满足sin(α＋20°)＝1，则锐角α的度数为(　　)
A．10° B．25° C．40° D．45°
9.下列各式中，不成立的是(　　)
A．cos60°＝2sin30°
B．sin15°＝cos75°
C．tan30°·tan60°＝1
D．sin230°＋cos230°＝1
10.对于任意锐角α，下列结论正确的是(　　)
A．sin αcos α D．tan α≥cos α
11.【2020·凉山州】如图所示，△ABC的顶点在正方形网格的格点上，则tanA的值为(　　)
A. B. C．2 D．2
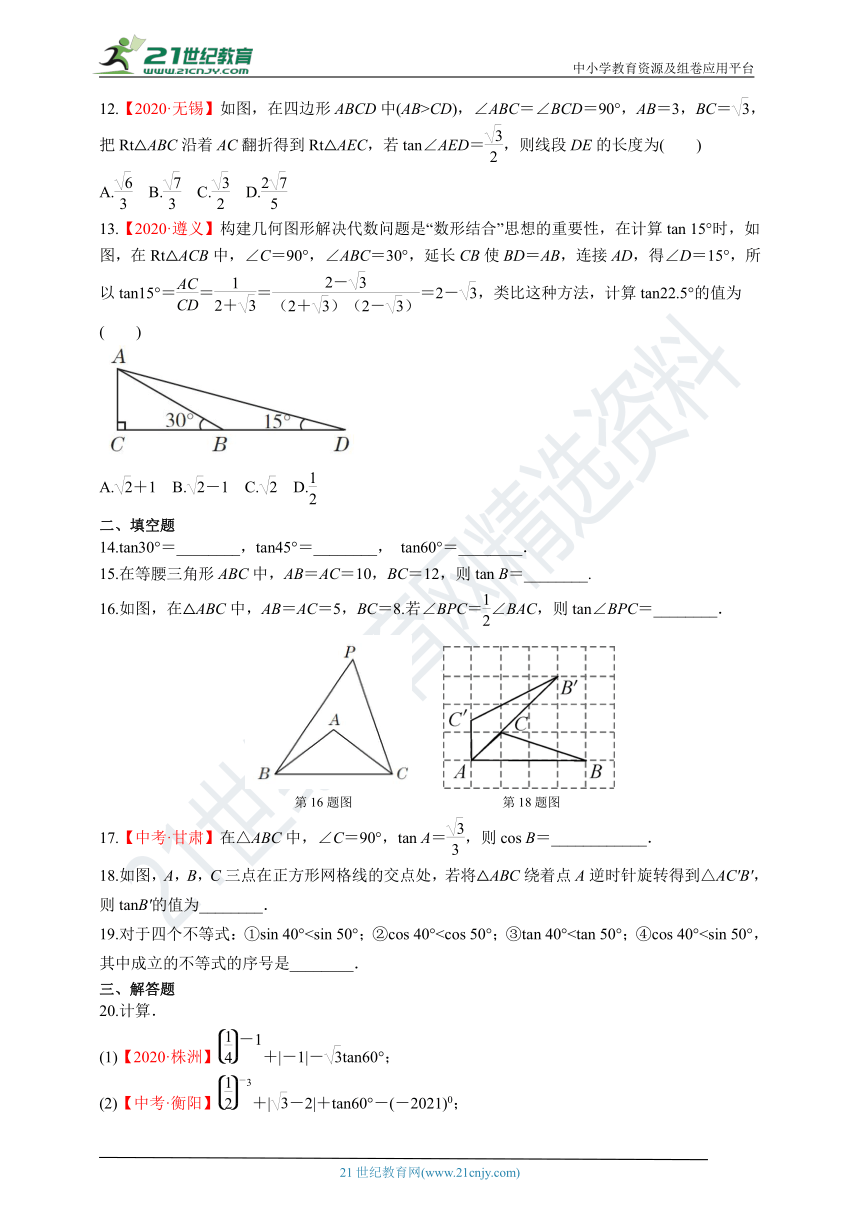
12.【2020·无锡】如图，在四边形ABCD中(AB>CD)，∠ABC＝∠BCD＝90°，AB＝3，BC＝，把Rt△ABC沿着AC翻折得到Rt△AEC，若tan∠AED＝，则线段DE的长度为(　　)
A. B. C. D.
13.【2020·遵义】构建几何图形解决代数问题是“数形结合”思想的重要性，在计算tan 15°时，如图，在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，得∠D＝15°，所以tan15°＝＝＝＝2－，类比这种方法，计算tan22.5°的值为(　　)
A.＋1 B.－1 C. D.
二、填空题
14.tan30°＝________，tan45°＝________， tan60°＝________．
15.在等腰三角形ABC中，AB＝AC＝10，BC＝12，则tan B＝________.
16.如图，在△ABC中，AB＝AC＝5，BC＝8.若∠BPC＝∠BAC，则tan∠BPC＝________．
第16题图 第18题图
17.【中考·甘肃】在△ABC中，∠C＝90°，tan A＝，则cos B＝____________．
18.如图，A，B，C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC'B'，则tanB'的值为________．
19.对于四个不等式：①sin 40°三、解答题
20.计算．
(1)【2020·株洲】＋|－1|－tan60°；
(2)【中考·衡阳】＋|－2|＋tan60°－(－2021)0；
(3)【2021·遂宁】计算：
(4)sin45°·cos45°＋＋3tan230°－.
(5)；
(6).
21.在如图所示的直角三角形中，我们知道sin α＝，cos α＝，tan α＝.
(1)试探究sin α，cos α与tan α之间的关系；
(2)请你利用上面探究的结论解答下面的问题：已知α为锐角，且tan α＝.求的值．
22.在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，∠C＝90°.若定义cot A＝＝，则称它为∠A的余切，我们把sin A，cos A，tan A，cot A叫作∠A的三角函数．根据这个定义解答下列问题：
(1)cot30°＝________；
(2)已知tan A＝，其中∠A为锐角，试求cot A的值；
(3)试说明：tanA＝cot(90°－∠A)．
23.【2020·黄冈】已知：如图，一次函数的图象与反比例函数的图象交于A，B两点，与y轴正半轴交于点C，与x轴负半轴交于点D，OB＝，tan∠DOB＝.
(1)求反比例函数的表达式；
(2)当S△ACO＝S△OCD时，求点C的坐标．
24.如图，在直角梯形ABCD中，AB∥DC，∠DAB＝90°，AB＝8，CD＝5，BC＝3.
(1)求梯形ABCD的面积；
(2)连接BD，求∠DBC的正切值．
25.有两张完全重合的矩形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图①)，连接BD，MF，若此时他测得BD＝8 cm，∠ADB＝30°.
(1)请直接写出AF的长；
(2)小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得到△AB1D1，AD1交FM于点K(如图②)，设旋转角为β(0°<β<90°)，当△AFK为等腰三角形时，求△AFK的面积(保留根号)．
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·黄冈】下列运算结果正确的是(　D　)
A．3a3·2a2＝6a6 B．(－2a)2＝－4a2 C．tan45°＝ D．cos30°＝
2.在等腰△ABC中，∠C＝90°，则tanB＝(　D　)
A. B. C. D．1
3.如图，在Rt△ABC中，∠C＝90°，若AC＝4，BC＝3，则下列结论中正确的是(　C　)
A．sinA＝ B．cosA＝ C．tanA＝ D．cosA＝
第3题图 第4题图 第11题图 第12题图
4.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，则下列不能表示tan A的是(　　)
A. B. C. D.
【点拨】∵在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，
∴易得△ACD∽△ABC∽△CBD.
∴∠A＝∠BCD.
在Rt△ACD中，tan A＝.
在Rt△BCD中，tan A＝tan ∠BCD＝.
在Rt△ABC中，tan A＝.
【答案】C
5.在Rt△ABC中，∠ACB＝90°，AB＝，tanB＝2，则AC的长为(　B　)
A．1 B．2 C. D．2
【点拨】在Rt△ABC中，∠ACB＝90°，tan B＝2，∴＝2，∴BC＝AC，由勾股定理，得AB2＝AC2＋BC2，即()2＝AC2＋，解得AC＝2(负值已舍去)．
6.在Rt△ABC中，∠C＝90°，a＝1，b＝，则∠A的度数为(　A　)
A．30° B．45° C．50° D．60°
【点拨】tan A＝＝＝.∴∠A＝30°.不能准确选用合适的边角关系式与对30°，60°角的正切值不能准确区分是本题的易错点．
7.【中考·包头】计算sin245°＋cos30°·tan60°，其结果是(　A　)
A．2 B．1 C. D.
8.已知锐角α满足sin(α＋20°)＝1，则锐角α的度数为(　B　)
A．10° B．25° C．40° D．45°
【点拨】∵sin(α＋20°)＝1，
∴sin (α＋20°)＝.∵α为锐角，
∴α＋20°＝45°，∴α＝45°－20°＝25°.
9.下列各式中，不成立的是(　A　)
A．cos60°＝2sin30°
B．sin15°＝cos75°
C．tan30°·tan60°＝1
D．sin230°＋cos230°＝1
【点拨】A.cos 60°＝sin 30°，错误； B．sin 15°＝cos 75°，正确；C.tan 30°·tan 60°＝1，正确；D.sin230°＋cos230°＝1，正确．
10.对于任意锐角α，下列结论正确的是(　A　)
A．sin αcos α D．tan α≥cos α
11.【2020·凉山州】如图所示，△ABC的顶点在正方形网格的格点上，则tanA的值为(　　)
A. B. C．2 D．2
【点拨】如图，连接BD，由网格的特点可得，
BD⊥AC，∵AD＝＝2，BD＝
＝，∴tan A＝＝＝，故选A.
12.【2020·无锡】如图，在四边形ABCD中(AB>CD)，∠ABC＝∠BCD＝90°，AB＝3，BC＝，把Rt△ABC沿着AC翻折得到Rt△AEC，若tan∠AED＝，则线段DE的长度为(　B　)
A. B. C. D.
【点拨】如图，延长ED交AC于点M，过点M作MN⊥AE于点N，设MN＝m，
∵tan∠AED＝，∴＝，∴NE＝2m，
∵∠ABC＝90°，AB＝3，BC＝，∴易得∠CAB＝30°.由翻折可知：∠EAC＝30°，∴AM＝2MN＝2m，∴AN＝MN＝3m，
∵AE＝AB＝3，∴5m＝3，∴m＝，
∴MN＝，AM＝，易知AC＝2，
∴CM＝AC－AM＝，
∵MN＝，NE＝2m＝，
∴EM＝＝，
∵∠ABC＝∠BCD＝90°，∴CD∥AB，∴∠DCA＝∠CAB＝30°，易知∠ECA＝∠BCA＝60°，
∴∠ECD＝30°，∴CD是∠ECM的平分线，
∴＝＝，∵CE＝BC＝，
∴＝，解得ED＝.故选B.
13.【2020·遵义】构建几何图形解决代数问题是“数形结合”思想的重要性，在计算tan 15°时，如图，在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，得∠D＝15°，所以tan15°＝＝＝＝2－，类比这种方法，计算tan22.5°的值为(　B　)
A.＋1 B.－1 C. D.
【点拨】如图，在Rt△ACB中，∠C＝90°，∠ABC＝45°，延长CB使BD＝AB，连接AD，得∠D＝22.5°.
设AC＝BC＝1，则AB＝BD＝，
∴tan22.5°＝＝＝－1.
二、填空题
14.tan30°＝________，tan45°＝________， tan60°＝________．
【答案】；1；
15.在等腰三角形ABC中，AB＝AC＝10，BC＝12，则tanB＝________.
【点拨】本题易忽略求正切值的前提是将∠B放在一个直角三角形中．
【答案】
16.如图，在△ABC中，AB＝AC＝5，BC＝8.若∠BPC＝∠BAC，则tan∠BPC＝________．
【答案】
第16题图 第18题图
17.【中考·甘肃】在△ABC中，∠C＝90°，tan A＝，则cos B＝____________．
【点拨】利用三角函数的定义及勾股定理求解．∵在△ABC中，∠C＝90°，tan A＝，设BC＝x，AC＝3x，则AB＝2x，∴cosB＝＝.
【答案】
18.如图，A，B，C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC'B'，则tanB'的值为________．
【答案】
19.对于四个不等式：①sin40°【点拨】由锐角的正弦值随锐角度数的增大而增大，余弦值随锐角度数的增大而减小，正切值随锐角度数的增大而增大，得sin40°＜sin50°，cos40°＞cos50°，tan40°＜tan50°，故①③正确，②错误．∵cos40°＝sin50°，故④错误．
【答案】①③
三、解答题
20.计算．
(1)【2020·株洲】＋|－1|－tan60°；
解：原式＝4＋1－×＝4＋1－3＝2.
(2)【中考·衡阳】＋|－2|＋tan 60°－(－2021)0；
解：原式＝8＋2－＋－1＝9.
(3)【2021·遂宁】计算：
【解析】解：
(4)sin45°·cos45°＋＋3tan230°－.
原式＝×＋＋3×－＝＋＋＋1－＝2.
(5)；
原式＝＝＝1.
(6).
原式＝＝＝1.
21.在如图所示的直角三角形中，我们知道sin α＝，cos α＝，tan α＝.
(1)试探究sinα，cosα与tanα之间的关系；
解：∵sin α＝，cos α＝，tan α＝，
∴＝＝，∴tan α＝.
(2)请你利用上面探究的结论解答下面的问题：已知α为锐角，且tan α＝.求的值．
解：∵tan α＝，∴＝，
∴2sin α＝cos α，
∴＝＝－.
22.在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，∠C＝90°.若定义cot A＝＝，则称它为∠A的余切，我们把sin A，cos A，tan A，cot A叫作∠A的三角函数．根据这个定义解答下列问题：
(1)cot 30°＝________；
【答案】
(2)已知tan A＝，其中∠A为锐角，试求cot A的值；
解：在Rt△ABC中，∠C＝90°，
∵tan A＝＝，
∴可设BC＝3k，则AC＝4k，
∴cot A＝＝＝.
(3)试说明：tan A＝cot(90°－∠A)．
解：在Rt△ABC中，∠C＝90°，
则∠A＋∠B＝90°，
即∠B＝90°－∠A.
∵tan A＝，cot B＝，
∴tan A＝cot B，
即tan A＝cot (90°－∠A)．
23.【2020·黄冈】已知：如图，一次函数的图象与反比例函数的图象交于A，B两点，与y轴正半轴交于点C，与x轴负半轴交于点D，OB＝，tan∠DOB＝.
(1)求反比例函数的表达式；
解：分别过点B，A作BM⊥x轴，AN⊥y轴，垂足分别为点M，N，如图．
设反比例函数的表达式为y＝(k≠0)．
在Rt△BOM中，OB＝，tan∠DOB＝.
易得BM＝1，OM＝2.
∴点B的坐标为(－2，－1)，∴k＝(－2)×(－1)＝2.
∴反比例函数的表达式为y＝.
(2)当S△ACO＝S△OCD时，求点C的坐标．
解：∵S△ACO＝S△OCD，S△ACO＝×OC×AN，
S△OCD＝×OC×OD，∴OD＝2AN.
易得△ANC∽△DOC，∴＝＝.
设AN＝a，CN＝b，则OD＝2a，OC＝2b.
∵S△OAN＝|k|＝1＝ON·AN＝×3b×a，
∴ab＝.①易得△BMD∽△CNA，
∴＝，即＝，∴a＝.②
由①②可求得b1＝1，b2＝－(舍去)．
∴OC＝2，∴点C的坐标为(0，2)．
24.如图，在直角梯形ABCD中，AB∥DC，∠DAB＝90°，AB＝8，CD＝5，BC＝3.
(1)求梯形ABCD的面积；
【点拨】过C作CE⊥AB于E，推出四边形ADCE是矩形，得到AD＝CE，AE＝CD＝5，根据勾股定理得到CE＝＝6，于是得到梯形ABCD的面积＝×(5＋8)×6＝39；
解：过C作CE⊥AB于E，如图，
∵AB∥DC，∠DAB＝90°，∴∠D＝90°，
∴∠A＝∠D＝∠AEC＝90°，
∴四边形ADCE是矩形，
∴AD＝CE，AE＝CD＝5，
∴BE＝AB－AE＝3，
∵BC＝3，∴CE＝＝6，
∴梯形ABCD的面积＝×(5＋8)×6＝39；
(2)连接BD，求∠DBC的正切值．
【点拨】过C作CH⊥BD于H，由题可知△CDH∽△DBA，根据相似三角形的性质得到＝，根据勾股定理得到BD＝＝＝10，BH＝＝＝6，于是得到结论．
解：过C作CH⊥BD于H，如图，
∵CD∥AB，∴∠CDB＝∠ABD，
∵∠CHD＝∠A＝90°，∴△CDH∽△DBA，
∴＝，∵BD＝＝＝10，
∴＝，∴CH＝3，
∴BH＝＝＝6，
∴tan∠DBC＝＝＝.
25.有两张完全重合的矩形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图①)，连接BD，MF，若此时他测得BD＝8 cm，∠ADB＝30°.
(1)请直接写出AF的长；
解：AF＝4 cm.
(2)小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得到△AB1D1，AD1交FM于点K(如图②)，设旋转角为β(0°<β<90°)，当△AFK为等腰三角形时，求△AFK的面积(保留根号)．
解：当△AFK为等腰三角形时，分两种情况：
①当AK＝FK时，如图①.
过点K作KN⊥AF于点N，
则AN＝NF＝AF＝2 cm.
在Rt△NFK中，∠KNF＝90°，∠F＝30°，
∴KN＝NF·tan F＝2 cm.
∴△AFK的面积为AF·KN＝4 cm2；
②当AF＝FK时，如图②.过点K作KP⊥AF于点P.
在Rt△PFK中，
∠KPF＝90°，∠F＝30°，
∴KP＝KF＝2 cm.
∴△AFK的面积为AF·KP＝12 cm2.
综上所述，当△AFK为等腰三角形时，△AFK的面积为4 cm2或12 cm2.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)