4.3 解直角三角形 同步练习(含解析)
文档属性
| 名称 | 4.3 解直角三角形 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 00:00:00 | ||
图片预览




文档简介
4.3 解直角三角形
一、选择题
1.下列条件中,可解的直角三角形是( )
A.已知b=3,∠C=90°
B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90°
D.已知∠B=15°,c=6,
2.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边.下列结论中错误的是( )
A.a= B.a=c·sin A C.c= D.b=a·tanB
3.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cosA的值是( )
A. B. C. D.
第3题图 第4题图 第5题图
4.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
5.【2019·凉山州】如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为( )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为( )
A.90° B.60° C.45° D.30°
7.【2020·福建改编】等腰三角形ABC的底边与底边上的中线的比是2∶,则△ABC的顶角为( )
A.60° B.90° C.120° D.150°
8.如图,在△ABC中,∠A=30°,tanB=,AC=2,则AB的长是( )
A.4 B.3+ C.5 D.2+2
第8题图 第11题图 第12题图
9.【2020·铜仁】已知等边三角形一边上的高为2,则它的边长为( )
A.2 B.3 C.4 D.4
10.在△ABC中,已知∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,c=,则下列解该直角三角形所得的结果中完全正确的一组是( )
A.∠A=30°,∠B=60°,b= B.∠A=30°,∠B=60°,b=
C.∠A=45°,∠B=45°,b= D.∠A=30°,∠B=60°,b=
11.如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,则AB的长为( )
A.4 B.3 C.5 D.4
12.如图,要在宽AB为22 m的道路两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应该设计为( )
A.(11-2)m B.(11-2)m C.(11-2)m D.(11-4)m
二、填空题
13.【2020·南通】如图,测角仪CD竖直放在距建筑物AB底部5 m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为________m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠A=45°,AC=,AB=+1,则边BC的长为________.
15.【中考·乐山】如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB边的长为________.
16.在△ABC中,AB=2,AC=2,∠B=30°,则BC的长为________.
17.【2020·枣庄】如图,人字梯AB,AC的长都为2 m,当α=50°时,人字梯顶端离地面的高度AD约是________m(结果精确到0.1 m,参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19).
第17题图 第18题图
18.【2020·荆州】“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”的号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了________km.
三、解答题
19.如图,在△ABC中,∠B=60°,AB=2,BC=3,AD⊥BC,垂足为D,求AC的长.
20.如图,在△ABC中,AD是BC边上的高,tan C=,AC=3 ,AB=4,求△ABC的周长.
21.【中考·襄阳】如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
22.【2021·广东】如图,在中,,作的垂直平分线交于点,延长至点,使.
(1)若,求的周长;
(2)若,求的值.
23.【2021·上海】如图,已知在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
24.如图,在平面直角坐标系中,点A在第一象限内,点B的坐标为(3,0),OA=2,∠AOB=60°.
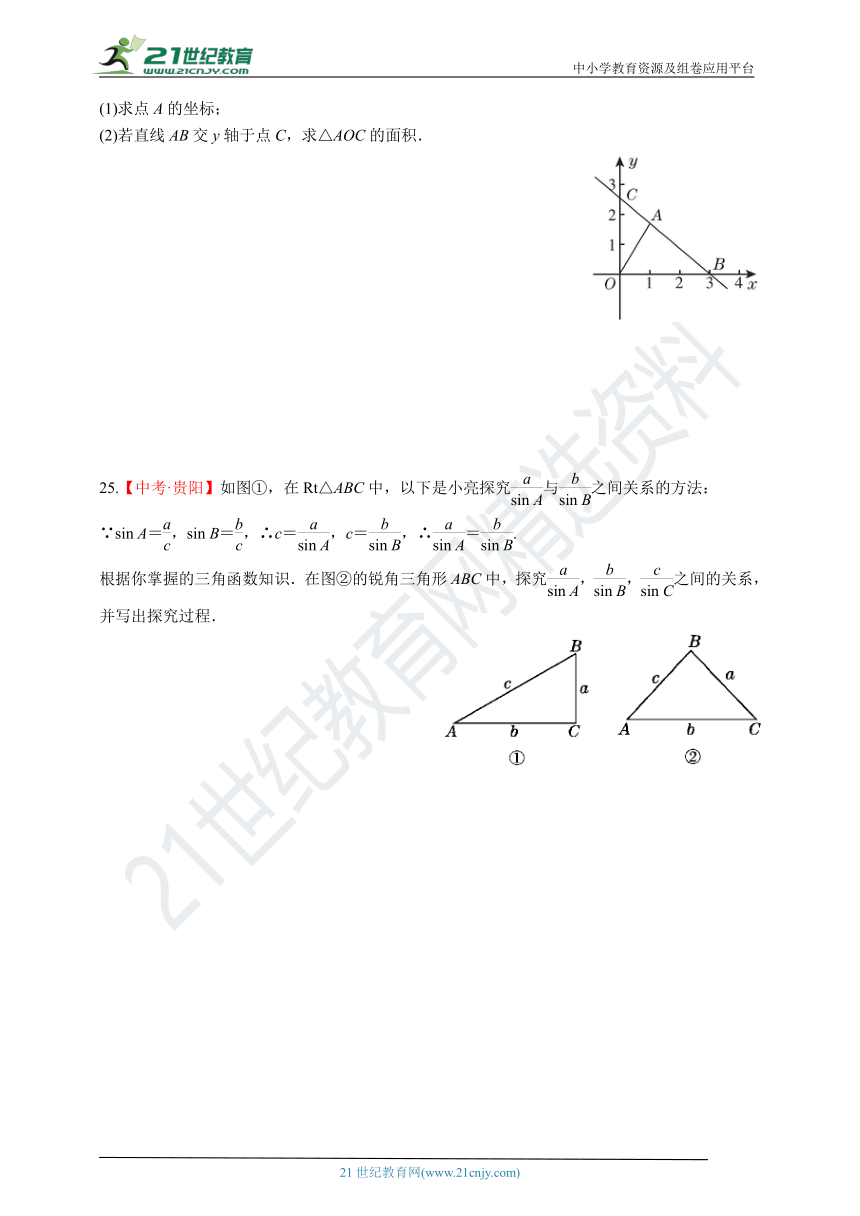
(1)求点A的坐标;
(2)若直线AB交y轴于点C,求△AOC的面积.
25.【中考·贵阳】如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sin A=,sin B=,∴c=,c=,∴=.
根据你掌握的三角函数知识.在图②的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列条件中,可解的直角三角形是( C )
A.已知b=3,∠C=90°
B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90°
D.已知∠B=15°,c=6,
2.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边.下列结论中错误的是( )
A.a= B.a=c·sinA C.c= D.b=a·tanB
【点拨】在Rt△ABC中,tan A=,∴a=b·tan A,选项A错误;∵sin A=,∴a=c·sin A, 选项B正确;
∵cos A=,∴c=,选项C正确;∵tan B=,∴b=a·tan B, 选项D正确.
【答案】A
3.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cosA的值是( D )
A. B. C. D.
第3题图 第4题图 第5题图
4.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )
A. B.4 C.8 D.4
5.【2019·凉山州】如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为( D )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为( B )
A.90° B.60° C.45° D.30°
7.【2020·福建改编】等腰三角形ABC的底边与底边上的中线的比是2∶,则△ABC的顶角为( A )
A.60° B.90° C.120° D.150°
8.如图,在△ABC中,∠A=30°,tanB=,AC=2,则AB的长是( C )
A.4 B.3+ C.5 D.2+2
第8题图 第11题图 第12题图
9.【2020·铜仁】已知等边三角形一边上的高为2,则它的边长为( C )
A.2 B.3 C.4 D.4
10.在△ABC中,已知∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,c=,则下列解该直角三角形所得的结果中完全正确的一组是( C )
A.∠A=30°,∠B=60°,b= B.∠A=30°,∠B=60°,b=
C.∠A=45°,∠B=45°,b= D.∠A=30°,∠B=60°,b=
11.如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,则AB的长为( A )
A.4 B.3 C.5 D.4
【点拨】如图,过点A作AD⊥BC于点D.在Rt△ACD中,
∠C=45°,AC=2 ,∴AD=AC·sin 45°=2.∵在Rt△ABD中,∠B=30°,∴sin 30°=,∴AB==4.
12.如图,要在宽AB为22 m的道路两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应该设计为( D )
A.(11-2)m B.(11-2)m C.(11-2)m D.(11-4)m
【点拨】如图,延长OD,BC交于点P.
易知∠ODC=∠B=90°,∠P=30°,OB=11 m,CD=2 m,∴在Rt△CPD中,DP==2 m, PC==4 m.
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO.∴=.
∴PB===11(m),
∴BC=PB-PC=(11-4)m.
二、填空题
13.【2020·南通】如图,测角仪CD竖直放在距建筑物AB底部5 m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为________m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
【点拨】如图,过点D作DE⊥AB,垂足为E,则DE=BC=5 m,DC=BE=1.5 m,
在Rt△ADE中,∵tan∠ADE=,
∴AE=tan∠ADE·DE=tan 50°×5≈5.95 m,
∴AB=AE+BE≈5.95+1.5≈7.5(m).
【答案】7.5
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠A=45°,AC=,AB=+1,则边BC的长为________.
【答案】2
15.【中考·乐山】如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB边的长为________.
【答案】
16.在△ABC中,AB=2,AC=2,∠B=30°,则BC的长为________.
【答案】4或2
17.【2020·枣庄】如图,人字梯AB,AC的长都为2 m,当α=50°时,人字梯顶端离地面的高度AD约是________m(结果精确到0.1 m,参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19).
【答案】1.5
第17题图 第18题图
18.【2020·荆州】“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”的号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了________km.
【点拨】过D点作DF⊥BC.
设EF=x km,则DF=x km,BF=x km,
在Rt△BFD中,BD==x km,
∵D地在AB正中位置,∴AB=2BD=x km.
∵tan∠ABC=,∴cos∠ABC=,
∴=,解得x=3.
即BC=8 km,AC=6 km,AB=10 km,
∴小张某天沿A→C→E→B→D→A路线跑一圈,他跑了6+8+10=24(km).
【答案】24
三、解答题
19.如图,在△ABC中,∠B=60°,AB=2,BC=3,AD⊥BC,垂足为D,求AC的长.
解:∵AD⊥BC,垂足为D,∴∠ADB=∠ADC=90°.
在Rt△ABD中,∠ADB=90°,∠B=60°,AB=2,
∴sin B===,cos B===,
解得AD=,BD=1.
∵BC=3,∴CD=2.
在Rt△ADC中,AC==.
20.如图,在△ABC中,AD是BC边上的高,tan C=,AC=3 ,AB=4,求△ABC的周长.
解:在Rt△ADC中,tan C==,
设AD=k,则CD=2k,AC==k.
∵AC=3,∴k=3,解得k=3,
∴AD=3,CD=6.
在Rt△ABD中,BD===,
∴△ABC的周长=AB+AC+BD+CD=4+3++6=10+3+.
21.【中考·襄阳】如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
解:如图,过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°.
在Rt△ACE中,
CE=AC·cos C=1,∴AE=CE=1.
在Rt△ABE中,tan B=,即=,
∴BE=3AE=3,∴BC=BE+CE=4.
(2)sin∠ADC的值.
解:∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD-CE=1.
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
22.【2021·广东】如图,在中,,作的垂直平分线交于点,延长至点,使.
(1)若,求的周长;
(2)若,求的值.
解:(1)如图,连接BD,设BC垂直平分线交BC于点F,DF为BC垂直平分线,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵CE=AB,
∴C△ABD=AC+CE=AE=1.
(2)设AD=k,则BD=3k,
又∵BD=CD,∴AC=AD+CD=4k
在Rt△ABC中,由勾股定理可得AB=2k
∴tan∠ABC==
23.【2021·上海】如图,已知在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
【考点】解直角三角形,中位线,勾股定理
【解答】解:(1)∵AC⊥BD cos∠ABC=,BC=8
∴AB=8×=10,由勾股定理得:AC=6
(2)过F作FG⊥CD于G点,
AC=6,CD=4,由勾股定理得:AD=2
∵BF为AD边上的中线
∴F为AD中点
∵FG⊥BD,AC⊥BD
∴FG∥AC,FG为△ACD的中位线
∴G为CD中点
∴BG=BC+CG=8-2=10,FG=AC=3
∴tan∠FBD==
24.如图,在平面直角坐标系中,点A在第一象限内,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
解:如图,过点A作AD⊥x轴,垂足为D.
∵OA=2,∠AOB=60°,
∴在Rt△OAD中,sin60°=,
cos60°=.∴AD=OA·sin60°=2sin60°=2×=,
OD=OA·cos60°=2cos60°=2×=1.
∴点A的坐标是(1,).
(2)若直线AB交y轴于点C,求△AOC的面积.
解:设直线AB的表达式为y=kx+b.∵直线AB过点A(1,)和B(3,0),
∴解得
∴直线AB的表达式为y=-x+. 令x=0,则y=.
∴OC=.∴S△AOC=OC·OD=××1=.
【点拨】过平面直角坐标系中的一点向x轴或向y轴作垂线是求点的坐标及三角形的面积的主要方法.在直角三角形中运用三角函数的知识,求出相关线段的长是解题的关键.
25.【中考·贵阳】如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:∵sin A=,sin B=, ∴c=,c=,∴=.
根据你掌握的三角函数知识.在图②的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
解:==,探究过程:如图,过A作AD⊥BC,垂足为D.
在Rt△ABD中,sin B=,即AD=c·sin B,
在Rt△ADC中,sin C=,即AD=b·sin C,
∴c·sin B=b·sin C,即=.
同理可得=,
则==.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
一、选择题
1.下列条件中,可解的直角三角形是( )
A.已知b=3,∠C=90°
B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90°
D.已知∠B=15°,c=6,
2.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边.下列结论中错误的是( )
A.a= B.a=c·sin A C.c= D.b=a·tanB
3.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cosA的值是( )
A. B. C. D.
第3题图 第4题图 第5题图
4.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
5.【2019·凉山州】如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为( )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为( )
A.90° B.60° C.45° D.30°
7.【2020·福建改编】等腰三角形ABC的底边与底边上的中线的比是2∶,则△ABC的顶角为( )
A.60° B.90° C.120° D.150°
8.如图,在△ABC中,∠A=30°,tanB=,AC=2,则AB的长是( )
A.4 B.3+ C.5 D.2+2
第8题图 第11题图 第12题图
9.【2020·铜仁】已知等边三角形一边上的高为2,则它的边长为( )
A.2 B.3 C.4 D.4
10.在△ABC中,已知∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,c=,则下列解该直角三角形所得的结果中完全正确的一组是( )
A.∠A=30°,∠B=60°,b= B.∠A=30°,∠B=60°,b=
C.∠A=45°,∠B=45°,b= D.∠A=30°,∠B=60°,b=
11.如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,则AB的长为( )
A.4 B.3 C.5 D.4
12.如图,要在宽AB为22 m的道路两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应该设计为( )
A.(11-2)m B.(11-2)m C.(11-2)m D.(11-4)m
二、填空题
13.【2020·南通】如图,测角仪CD竖直放在距建筑物AB底部5 m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为________m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠A=45°,AC=,AB=+1,则边BC的长为________.
15.【中考·乐山】如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB边的长为________.
16.在△ABC中,AB=2,AC=2,∠B=30°,则BC的长为________.
17.【2020·枣庄】如图,人字梯AB,AC的长都为2 m,当α=50°时,人字梯顶端离地面的高度AD约是________m(结果精确到0.1 m,参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19).
第17题图 第18题图
18.【2020·荆州】“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”的号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了________km.
三、解答题
19.如图,在△ABC中,∠B=60°,AB=2,BC=3,AD⊥BC,垂足为D,求AC的长.
20.如图,在△ABC中,AD是BC边上的高,tan C=,AC=3 ,AB=4,求△ABC的周长.
21.【中考·襄阳】如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
22.【2021·广东】如图,在中,,作的垂直平分线交于点,延长至点,使.
(1)若,求的周长;
(2)若,求的值.
23.【2021·上海】如图,已知在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
24.如图,在平面直角坐标系中,点A在第一象限内,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交y轴于点C,求△AOC的面积.
25.【中考·贵阳】如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sin A=,sin B=,∴c=,c=,∴=.
根据你掌握的三角函数知识.在图②的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列条件中,可解的直角三角形是( C )
A.已知b=3,∠C=90°
B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90°
D.已知∠B=15°,c=6,
2.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边.下列结论中错误的是( )
A.a= B.a=c·sinA C.c= D.b=a·tanB
【点拨】在Rt△ABC中,tan A=,∴a=b·tan A,选项A错误;∵sin A=,∴a=c·sin A, 选项B正确;
∵cos A=,∴c=,选项C正确;∵tan B=,∴b=a·tan B, 选项D正确.
【答案】A
3.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cosA的值是( D )
A. B. C. D.
第3题图 第4题图 第5题图
4.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )
A. B.4 C.8 D.4
5.【2019·凉山州】如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为( D )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,AB=2,AC=,则∠B的度数为( B )
A.90° B.60° C.45° D.30°
7.【2020·福建改编】等腰三角形ABC的底边与底边上的中线的比是2∶,则△ABC的顶角为( A )
A.60° B.90° C.120° D.150°
8.如图,在△ABC中,∠A=30°,tanB=,AC=2,则AB的长是( C )
A.4 B.3+ C.5 D.2+2
第8题图 第11题图 第12题图
9.【2020·铜仁】已知等边三角形一边上的高为2,则它的边长为( C )
A.2 B.3 C.4 D.4
10.在△ABC中,已知∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,c=,则下列解该直角三角形所得的结果中完全正确的一组是( C )
A.∠A=30°,∠B=60°,b= B.∠A=30°,∠B=60°,b=
C.∠A=45°,∠B=45°,b= D.∠A=30°,∠B=60°,b=
11.如图,在△ABC中,∠B=30°,∠C=45°,AC=2 ,则AB的长为( A )
A.4 B.3 C.5 D.4
【点拨】如图,过点A作AD⊥BC于点D.在Rt△ACD中,
∠C=45°,AC=2 ,∴AD=AC·sin 45°=2.∵在Rt△ABD中,∠B=30°,∴sin 30°=,∴AB==4.
12.如图,要在宽AB为22 m的道路两边安装路灯,路灯的灯臂CD长2 m,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应该设计为( D )
A.(11-2)m B.(11-2)m C.(11-2)m D.(11-4)m
【点拨】如图,延长OD,BC交于点P.
易知∠ODC=∠B=90°,∠P=30°,OB=11 m,CD=2 m,∴在Rt△CPD中,DP==2 m, PC==4 m.
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO.∴=.
∴PB===11(m),
∴BC=PB-PC=(11-4)m.
二、填空题
13.【2020·南通】如图,测角仪CD竖直放在距建筑物AB底部5 m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为________m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
【点拨】如图,过点D作DE⊥AB,垂足为E,则DE=BC=5 m,DC=BE=1.5 m,
在Rt△ADE中,∵tan∠ADE=,
∴AE=tan∠ADE·DE=tan 50°×5≈5.95 m,
∴AB=AE+BE≈5.95+1.5≈7.5(m).
【答案】7.5
第13题图 第14题图 第15题图
14.如图,在△ABC中,∠A=45°,AC=,AB=+1,则边BC的长为________.
【答案】2
15.【中考·乐山】如图,在△ABC中,∠B=30°,AC=2,cos C=,则AB边的长为________.
【答案】
16.在△ABC中,AB=2,AC=2,∠B=30°,则BC的长为________.
【答案】4或2
17.【2020·枣庄】如图,人字梯AB,AC的长都为2 m,当α=50°时,人字梯顶端离地面的高度AD约是________m(结果精确到0.1 m,参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19).
【答案】1.5
第17题图 第18题图
18.【2020·荆州】“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”的号召,坚持在某环形步道上跑步.已知此步道外形近似于如图所示的Rt△ABC,其中∠C=90°,AB与BC间另有步道DE相连,D地在AB正中位置,E地与C地相距1km.若tan∠ABC=,∠DEB=45°,小张某天沿A→C→E→B→D→A路线跑一圈,则他跑了________km.
【点拨】过D点作DF⊥BC.
设EF=x km,则DF=x km,BF=x km,
在Rt△BFD中,BD==x km,
∵D地在AB正中位置,∴AB=2BD=x km.
∵tan∠ABC=,∴cos∠ABC=,
∴=,解得x=3.
即BC=8 km,AC=6 km,AB=10 km,
∴小张某天沿A→C→E→B→D→A路线跑一圈,他跑了6+8+10=24(km).
【答案】24
三、解答题
19.如图,在△ABC中,∠B=60°,AB=2,BC=3,AD⊥BC,垂足为D,求AC的长.
解:∵AD⊥BC,垂足为D,∴∠ADB=∠ADC=90°.
在Rt△ABD中,∠ADB=90°,∠B=60°,AB=2,
∴sin B===,cos B===,
解得AD=,BD=1.
∵BC=3,∴CD=2.
在Rt△ADC中,AC==.
20.如图,在△ABC中,AD是BC边上的高,tan C=,AC=3 ,AB=4,求△ABC的周长.
解:在Rt△ADC中,tan C==,
设AD=k,则CD=2k,AC==k.
∵AC=3,∴k=3,解得k=3,
∴AD=3,CD=6.
在Rt△ABD中,BD===,
∴△ABC的周长=AB+AC+BD+CD=4+3++6=10+3+.
21.【中考·襄阳】如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
解:如图,过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°.
在Rt△ACE中,
CE=AC·cos C=1,∴AE=CE=1.
在Rt△ABE中,tan B=,即=,
∴BE=3AE=3,∴BC=BE+CE=4.
(2)sin∠ADC的值.
解:∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD-CE=1.
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
22.【2021·广东】如图,在中,,作的垂直平分线交于点,延长至点,使.
(1)若,求的周长;
(2)若,求的值.
解:(1)如图,连接BD,设BC垂直平分线交BC于点F,DF为BC垂直平分线,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵CE=AB,
∴C△ABD=AC+CE=AE=1.
(2)设AD=k,则BD=3k,
又∵BD=CD,∴AC=AD+CD=4k
在Rt△ABC中,由勾股定理可得AB=2k
∴tan∠ABC==
23.【2021·上海】如图,已知在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
【考点】解直角三角形,中位线,勾股定理
【解答】解:(1)∵AC⊥BD cos∠ABC=,BC=8
∴AB=8×=10,由勾股定理得:AC=6
(2)过F作FG⊥CD于G点,
AC=6,CD=4,由勾股定理得:AD=2
∵BF为AD边上的中线
∴F为AD中点
∵FG⊥BD,AC⊥BD
∴FG∥AC,FG为△ACD的中位线
∴G为CD中点
∴BG=BC+CG=8-2=10,FG=AC=3
∴tan∠FBD==
24.如图,在平面直角坐标系中,点A在第一象限内,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
解:如图,过点A作AD⊥x轴,垂足为D.
∵OA=2,∠AOB=60°,
∴在Rt△OAD中,sin60°=,
cos60°=.∴AD=OA·sin60°=2sin60°=2×=,
OD=OA·cos60°=2cos60°=2×=1.
∴点A的坐标是(1,).
(2)若直线AB交y轴于点C,求△AOC的面积.
解:设直线AB的表达式为y=kx+b.∵直线AB过点A(1,)和B(3,0),
∴解得
∴直线AB的表达式为y=-x+. 令x=0,则y=.
∴OC=.∴S△AOC=OC·OD=××1=.
【点拨】过平面直角坐标系中的一点向x轴或向y轴作垂线是求点的坐标及三角形的面积的主要方法.在直角三角形中运用三角函数的知识,求出相关线段的长是解题的关键.
25.【中考·贵阳】如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:∵sin A=,sin B=, ∴c=,c=,∴=.
根据你掌握的三角函数知识.在图②的锐角三角形ABC中,探究,,之间的关系,并写出探究过程.
解:==,探究过程:如图,过A作AD⊥BC,垂足为D.
在Rt△ABD中,sin B=,即AD=c·sin B,
在Rt△ADC中,sin C=,即AD=b·sin C,
∴c·sin B=b·sin C,即=.
同理可得=,
则==.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
