第4章　锐角三角形 章末复习（含答案）

中小学教育资源及组卷应用平台
第4章　锐角三角形
章末复习
一、选择题
1.如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是 (　　)
A．2 B. C. D.
第1题图 第2题图 第8题图 第9题图
2.已知，将如图所示的三角板的直角顶点放置在直线AB上的点O处，使斜边CD∥AB，则∠α的余弦值为 (　　)
A. B. C. D．1
3.在Rt△ABC中，∠C＝90°，BC＝，AC＝，则∠A等于(　　)
A．90° B．60° C．45° D．30°
4.锐角α满足sinα>，且tanα<，则α的取值范围为(　　)
A．30°＜α＜45° B．45°＜α＜60° C．60°＜α＜90° D．30°＜α＜60°
5.式子2cos30°－tan45°－的值是(　　)
A．2－2 B．0 C．2 D．2
6.在△ABC中，若cos A＝cos B＝，则△ABC是 (　　)
A．钝角三角形 B．锐角三角形 C．直角三角形 D．不能确定
7.△ABC中，∠B＝90°，AC＝，tanC＝，则BC边的长为(　　)
A．2 B．2 C. D．4
8.【中考·营口】如图，在四边形ABCD中，∠DAB＝90°，AD∥BC，BC＝AD，AC与BD交于点E，AC⊥BD，则tan∠BAC的值是 (　　)
A. B. C. D.
9.【2021·长春德惠期末】如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC＝α，∠ADC＝β，则竹竿AB与AD的长度之比为(　　)
A. B. C. D.
10.如图，已知在平行四边形ABCD中，AB＝a，BC＝b，∠B＝α，那么这个平行四边形的面积等于(　　)
A．absinα B．abcosα C．ab·tanα D.absinα
第10题图 第12题图 第13题图 第17题图
11.若α，β都是锐角，以下结论：①若α<β，则tan αA．①② B．①②③ C．①③④ D．①②③④
12.【2020·无锡】如图，在四边形ABCD中(AB>CD)，∠ABC＝∠BCD＝90°，AB＝3，BC＝，把Rt△ABC沿着AC翻折得到Rt△AEC，若tan∠AED＝，则线段DE的长度为(　　)
A. B. C. D.
二、填空题
13.如图，△ABC中，D为AB中点，DC⊥AC于点C，DE∥AC交BC于点E，若DE＝BD，则cosA＝________．
14.【滨州中考】在△ABC中，∠C＝90°，若tanA＝，则sinB＝________．
15.若α为锐角，且sinα＝3m－2，则m的取值范围是________．
16.【来宾期末】已知锐角A满足4sin2A＝3，则∠A＝________．
17.【柳州中考】如图，在△ABC中，sinB＝，tanC＝，若AB＝3，则AC的长为________．
18.如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.给出下列四个结论：①sinα＝sinB；②sinβ＝sinC；③sinB＝cosC；④sinα＝cosβ.其中正确结论的序号是________．
三、解答题
19.计算：(1)tan30°sin60°＋cos230°－sin245°tan45°.
(2)tan30°sin60°＋cos230°－sin245°tan45°；
(3)tan245°＋－3cos230°＋－.
(4)【百色期末】2cos45°－tan30°cos30°＋sin260°；
(5)tan30°cos60°＋tan45°cos30°.
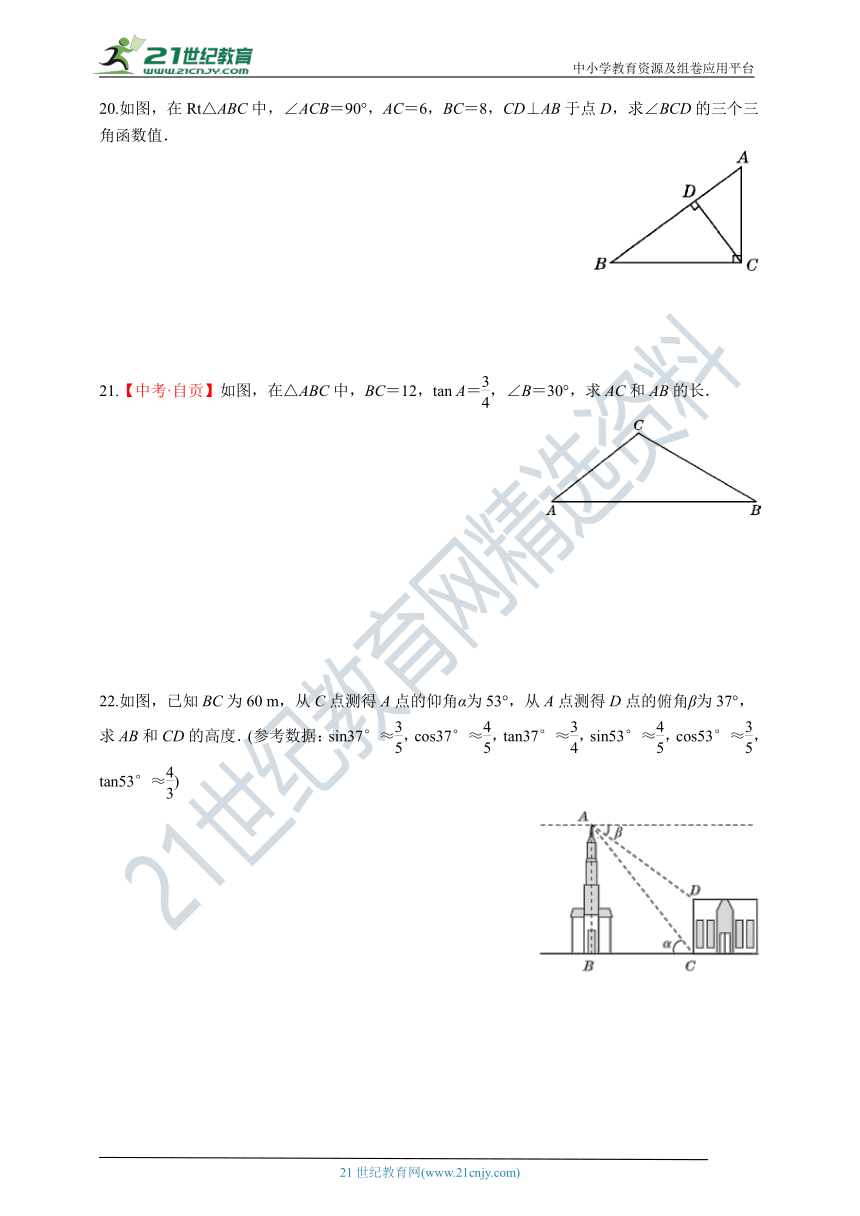
20.如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，CD⊥AB于点D，求∠BCD的三个三角函数值．
21.【中考·自贡】如图，在△ABC中，BC＝12，tan A＝，∠B＝30°，求AC和AB的长．
22.如图，已知BC为60 m，从C点测得A点的仰角α为53°，从A点测得D点的俯角β为37°，求AB和CD的高度．(参考数据：sin37°≈，cos37°≈，tan37°≈，sin53°≈，cos53°≈，tan53°≈)
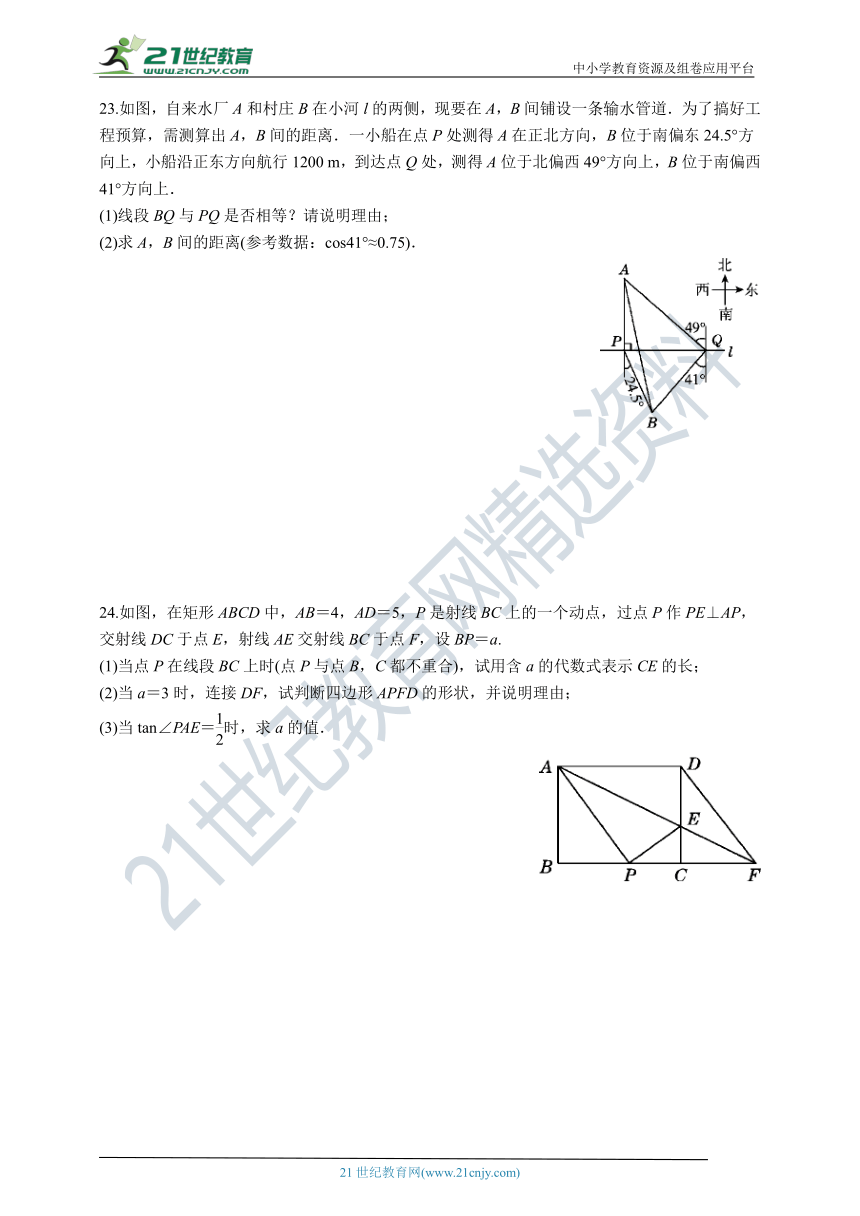
23.如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水管道．为了搞好工程预算，需测算出A，B间的距离．一小船在点P处测得A在正北方向，B位于南偏东24.5°方向上，小船沿正东方向航行1200 m，到达点Q处，测得A位于北偏西49°方向上，B位于南偏西41°方向上．
(1)线段BQ与PQ是否相等？请说明理由；
(2)求A，B间的距离(参考数据：cos41°≈0.75)．
24.如图，在矩形ABCD中，AB＝4，AD＝5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP＝a.
(1)当点P在线段BC上时(点P与点B，C都不重合)，试用含a的代数式表示CE的长；
(2)当a＝3时，连接DF，试判断四边形APFD的形状，并说明理由；
(3)当tan∠PAE＝时，求a的值．
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是 (　D　)
A．2 B. C. D.
第1题图 第2题图 第8题图 第9题图
2.已知，将如图所示的三角板的直角顶点放置在直线AB上的点O处，使斜边CD∥AB，则∠α的余弦值为 (　A　)
A. B. C. D．1
3.在Rt△ABC中，∠C＝90°，BC＝，AC＝，则∠A等于(　D　)
A．90° B．60° C．45° D．30°
4.锐角α满足sinα>，且tanα<，则α的取值范围为(　B　)
A．30°＜α＜45° B．45°＜α＜60° C．60°＜α＜90° D．30°＜α＜60°
5.式子2cos30°－tan45°－的值是(　B　)
A．2－2 B．0 C．2 D．2
6.在△ABC中，若cos A＝cos B＝，则△ABC是 (　B　)
A．钝角三角形 B．锐角三角形 C．直角三角形 D．不能确定
7.△ABC中，∠B＝90°，AC＝，tan C＝，则BC边的长为(　B　)
A．2 B．2 C. D．4
8.【中考·营口】如图，在四边形ABCD中，∠DAB＝90°，AD∥BC，BC＝AD，AC与BD交于点E，AC⊥BD，则tan∠BAC的值是 (　C　)
A. B. C. D.
9.【2021·长春德惠期末】如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC＝α，∠ADC＝β，则竹竿AB与AD的长度之比为(　B　)
A. B. C. D.
10.如图，已知在平行四边形ABCD中，AB＝a，BC＝b，∠B＝α，那么这个平行四边形的面积等于(　A　)
A．absinα B．abcosα C．ab·tanα D.absinα
【点拨】∵AB＝a，BC＝b，∠B＝α，
∴平行四边形ABCD的边BC上的高为a·sin α，
∴平行四边形ABCD的面积＝底×高＝b·a·sin α＝ab·sin α.
第10题图 第12题图 第13题图 第17题图
11.若α，β都是锐角，以下结论：①若α<β，则tan αA．①② B．①②③ C．①③④ D．①②③④
【点拨】①∵tan α随锐角α的增大而增大，∴若α＜β，则tan α＜tan β，此结论正确；
②∵cos α随锐角α的增大而减小，∴若α＜β，则cos α＞cos β，此结论错误；
③∵α与β互余，∴tan α·tan β＝1，此结论正确；
④∵α＋β＝90°，∴sin α＝cos (90°－α)＝cos β，此结论正确．
综上，正确的结论为①③④.
【答案】C
12.【2020·无锡】如图，在四边形ABCD中(AB>CD)，∠ABC＝∠BCD＝90°，AB＝3，BC＝，把Rt△ABC沿着AC翻折得到Rt△AEC，若tan∠AED＝，则线段DE的长度为(　　)
A. B. C. D.
【点拨】如图，延长CD交AE于F，过点D作DG⊥EF于G.
∵∠ABC＝90°，BC＝，AB＝3，
∴tan∠BAC＝＝.
∴∠BAC＝30°.
∵∠ABC＝∠DCB＝90°，∴CD∥AB，
∴∠DCA＝∠BAC＝30°，由题意可得CE＝BC＝，
∠AEC＝∠ABC＝90°，∠CAE＝∠CAB＝30°，
∴∠EFC＝60°. ∴EF＝＝1.
设GF＝x，则GD＝GF·tan 60°＝x.
∵tan ∠AED＝，∴＝＝，∴EG＝2x.
∵EF＝EG＋FG，∴1＝2x＋x，∴x＝.
∴EG＝，GD＝. ∴由勾股定理得ED＝.
故选B.
【答案】B
二、填空题
13.如图，△ABC中，D为AB中点，DC⊥AC于点C，DE∥AC交BC于点E，若DE＝BD，则cosA＝________．
【答案】
14.【滨州中考】在△ABC中，∠C＝90°，若tanA＝，则sinB＝________．
【答案】
15.若α为锐角，且sinα＝3m－2，则m的取值范围是________．
【答案】＜m＜1
16.【来宾期末】已知锐角A满足4sin2A＝3，则∠A＝________．
【答案】60°
17.【柳州中考】如图，在△ABC中，sinB＝，tanC＝，若AB＝3，则AC的长为________．
【答案】
18.如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.给出下列四个结论：①sinα＝sinB；②sinβ＝sinC；③sinB＝cosC；④sinα＝cosβ.其中正确结论的序号是________．
【点拨】∵∠BAC＝90°，AD⊥BC，∴∠α＋∠β＝90°，∠B＋∠β＝90°，∠B＋∠C＝90°，∴∠α＝∠B，∠β＝∠C，∴sinα＝sinB，故①正确；sinβ＝sinC，故②正确；
∵在Rt△ABC中，sinB＝，cosC＝，
∴sinB＝cosC，故③正确；
∵sinα＝sinB，cosβ＝cosC，
∴sinα＝cosβ，故④正确．
【答案】①②③④
三、解答题
19.计算：(1)tan 30°sin60°＋cos230°－sin245°tan45°.
解：原式＝×＋－×1＝＋－＝.
(2)tan30°sin60°＋cos230°－sin245°tan45°；
解：原式＝×＋－×1
＝＋－
＝．
(3)tan245°＋－3cos230°＋－.
解：原式＝×12＋－3×＋－1
＝＋4－3×＋2－1
＝3．
(4)【百色期末】2cos45°－tan30°cos30°＋sin260°；
解：原式＝2×－××＋
＝－＋
＝.
(5)tan30°cos60°＋tan45°cos30°.
解：原式＝×＋1×
＝＋
＝.
20.如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，CD⊥AB于点D，求∠BCD的三个三角函数值．
解：∵∠ACB＝90°，∴∠BCD＋∠ACD＝90°.
∵CD⊥AB，∴∠ACD＋∠A＝90°，∴∠BCD＝∠A.
由勾股定理，得AB＝＝10，
∴sin∠BCD＝sinA＝＝，
cos∠BCD＝cosA＝＝，
tan∠BCD＝tanA＝＝.
21.【中考·自贡】如图，在△ABC中，BC＝12，tan A＝，∠B＝30°，求AC和AB的长．
解：如图，过点C作CD⊥AB，交AB于点D，
在Rt△BCD中，∠B＝30°，BC＝12，
∴CD＝BC·sin B＝12×＝6，BD＝BC·cos B＝12×＝6.
∴在Rt△ACD中，tan A＝＝＝，∴AD＝8，
∴AC＝＝＝10，AB＝AD＋BD＝8＋6.
22.如图，已知BC为60 m，从C点测得A点的仰角α为53°，从A点测得D点的俯角β为37°，求AB和CD的高度．(参考数据：sin37°≈，cos37°≈，tan37°≈，sin53°≈，cos53°≈，tan53°≈)
解：如图，过点D作DE⊥AB于点E，
则DE＝BC＝60 m，BE＝CD.
∵在Rt△ABC中，tan α＝，α＝53°，
∴≈，即≈，∴AB≈80 m.
∵在Rt△ADE中，tan∠ADE＝，∠ADE＝β＝37°，
∴≈，即≈，∴AE≈45 m，
∴CD＝BE＝AB－AE≈80－45＝35 (m)．
答：AB和CD的高度分别约为80 m和 35 m.
23.如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水管道．为了搞好工程预算，需测算出A，B间的距离．一小船在点P处测得A在正北方向，B位于南偏东24.5°方向上，小船沿正东方向航行1200 m，到达点Q处，测得A位于北偏西49°方向上，B位于南偏西41°方向上．
(1)线段BQ与PQ是否相等？请说明理由；
解：相等．理由如下：
由已知条件易知，∠BPQ＝90°－24.5°＝65.5°，∠PQB＝90°－41°＝49°，
∴∠PBQ＝180°－65.5°－49°＝65.5°.
∴∠PBQ＝∠BPQ.∴BQ＝PQ.
(2)求A，B间的距离(参考数据：cos 41°≈0.75)．
解：由(1)得BQ＝PQ＝1 200 m.
由已知条件易知∠AQP＝90°－49°＝41°.
∴∠AQP＋∠PQB＝90°.
在Rt△APQ中，AQ＝≈＝1 600(m)．
∴在Rt△AQB中，
AB＝≈＝2 000(m)．
∴A，B间的距离约是2000 m.
24.如图，在矩形ABCD中，AB＝4，AD＝5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP＝a.
(1)当点P在线段BC上时(点P与点B，C都不重合)，试用含a的代数式表示CE的长；
解：设CE＝y.
∵四边形ABCD是矩形，∴BC＝AD＝5，∠B＝∠BCD＝90°.
∵BP＝a，∴PC＝5－a.
∵AP⊥PE，∴∠APE＝90°，∴∠APB＋∠CPE＝90°，
又∵∠APB＋∠BAP＝180°－∠B＝90°，
∴∠BAP＝∠CPE，∴△ABP∽△PCE，
∴＝，即＝，
∴y＝，即CE＝.
(2)当a＝3时，连接DF，试判断四边形APFD的形状，并说明理由；
解：四边形APFD是菱形，理由如下：当a＝3时，点P在线段BC上，由(1)可得CE＝＝.
∵四边形ABCD是矩形，∴AD∥BF，CD＝AB＝4，
∴△AED∽△FEC，DE＝.
∴＝，即＝，∴CF＝3，
又∵PC＝5－3＝2，∴PF＝PC＋CF＝5.
∴PF＝AD，∴四边形APFD是平行四边形，
在Rt△APB中，AB＝4，BP＝3，∠B＝90°，
∴AP＝5＝PF，∴四边形APFD是菱形．
(3)当tan∠PAE＝时，求a的值．
解：根据tan ∠PAE＝可得＝2.
当点P在线段BC上时，由(1)知△ABP∽△PCE，
∴＝＝2，即＝2，解得a＝3；
当点P在BC的延长线上时，PC＝PB－BC＝a－5，
易证△ABP∽△PCE，∴＝＝2，即＝2，解得a＝7.
综上，a＝3或a＝7.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)