苏科版八年级数学上册 3.1 勾股定理(2)(教案)
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理(2)(教案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 07:50:37 | ||
图片预览


文档简介
3.1 勾股定理(2)
教学目标 1.让学生经历验证探索勾股定理的过程,培养学生主动探究意识,发展合情推理的能力,体会数形结合思想. 2.经历用多种拼图方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考与表达的能力,感受勾股定理蕴含的数学文化和丰富的数学思想.
教学重点 通过综合运用已有知识解决问题的过程,加深对数形结合的思想的认识.
教学难点 通过拼图验证勾股定理的过程,使学生获得一些研究问题与合作交流的方法与经验.
教学过程(教师) 学生活动 设计思路
(一)创设情境 提出问题 同学们,上一节可我们学习了著名的数学定理——《勾股定理》.大家还记得勾股定理的内容是什么吗?它用符号语言又可以如何表示呢? 上一节课,我们主要通过观察、测量、猜想得到了勾股定理.我们知道仅仅靠观察、测量、猜想并不严谨.因此,本节课我们一起来验证勾股定理. 复习回顾,兴趣盎然. 这是对上一节课勾股定理内容的回顾,从学生的原有认知出发,揭示这节课产生的根源,符合学生的认知心理,也自然地引出本节课的目标.
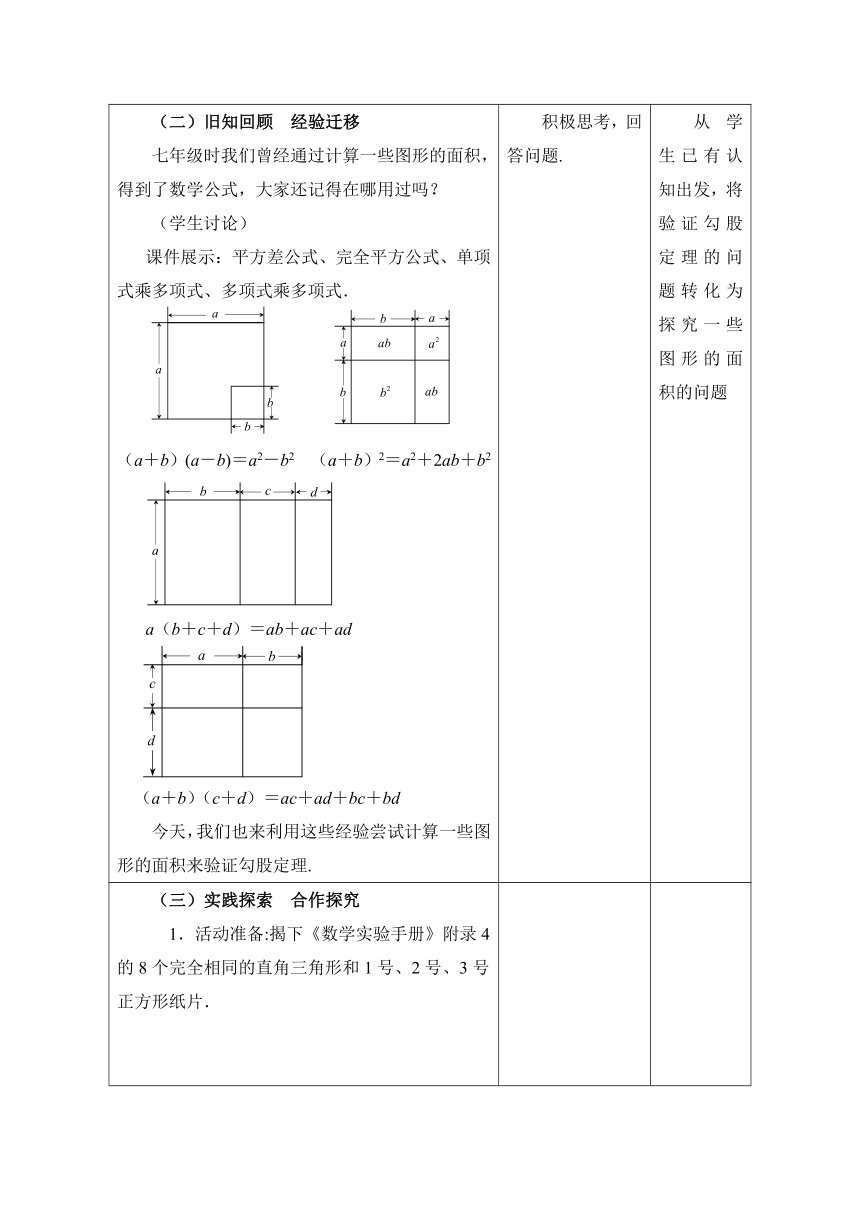
(二)旧知回顾 经验迁移 七年级时我们曾经通过计算一些图形的面积,得到了数学公式,大家还记得在哪用过吗? (学生讨论) 课件展示:平方差公式、完全平方公式、单项式乘多项式、多项式乘多项式. (a+b)(a-b)=a2-b2 (a+b)2=a2+2ab+b2 a(b+c+d)=ab+ac+ad (a+b)(c+d)=ac+ad+bc+bd 今天,我们也来利用这些经验尝试计算一些图形的面积来验证勾股定理. 积极思考,回答问题. 从学生已有认知出发,将验证勾股定理的问题转化为探究一些图形的面积的问题
(三)实践探索 合作探究 1.活动准备:揭下《数学实验手册》附录4的8个完全相同的直角三角形和1号、2号、3号正方形纸片. (不妨设两直角边分别为a、b ,且a≤b ,斜边为 c) 2. 活动一: 选用4个完全相同的直角三角形和1 号正方形纸片,拼成1个新的正方形; 选用4个完全相同的直角三角形和2 号、3号正方形纸片,拼成1个新的正方形; (3) 你能利用所拼成的2个正方形证明验证勾股定理吗? 其实,再来观察这两幅图形,两幅图形都是边长为a+b的正方形,面积相等.减去里面四个完全相同的直角三角形,剩余的部分面积也应该相等.而第一幅图形中剩余部分是正方形,边长为c,因此剩余部分面积为c2,第二幅图形中剩余部分为两个边长分别为a,b的正方形,面积和为a2+b2.这样可以不用动笔计算,直接得到勾股定理. 这是勾股定理最早的证明,它是著名的毕达哥拉斯学派的贡献,因此这种证明勾股定理的方法叫做“毕达哥拉斯证法”.这种证法不仅最早,而且也是最直观的图形验证的方法,它可以不用图形之外的语言让我们看明白勾股定理的正确性. 然而,这种证明勾股定理的方法弊端是图形涉及两个正方形,图形构造不容易想到. 3.活动二: 你能只利用这一个图形验证勾股定理吗? 这种证明勾股定理的方法是我国数学家邹元治的证法,只用了毕达哥拉斯证法中的一个图形,就验证了勾股定理. 邹元治证法涉及的图形,也可以理解为用四个完全相同的直角三角形拼成了边长为c的正方形. 你还能只利用4个完全相同的直角三角形拼成边长为c的正方形验证勾股定理吗? 这个图案是我国古代著名的数学家赵爽在注解《周髀算经》时所给出.因此人们为了纪念赵爽,将这副图案叫做赵爽弦图.这也是我国对于勾股定理的第一个证明,代表了我国古代数学的成就. 正因为如此,2002年世界数学家大会,正是以赵爽弦图为大会的会徽.它也像是一个转动的风车,欢迎全世界各国的数学家到我国进行思想的交流和智慧的碰撞. 以上活动中的验证方法至少涉及四个直角三角形,能否再简化证明的图形呢? 活动三: 你能只利用2个完全相同的直角三角形所拼 成的图形验证勾股定理吗? 这种证明勾股定理的方法是美国第二十届总统伽菲尔德的证法,人们为了纪念伽菲尔德,将这种证明勾股定理的方法,叫做总统证法.总统证法相比前面的验证方法,图形更加的简洁,明了. 其实,从古至今,人们对验证勾股定理的方法不断地探索创新,产生了许多的奇思妙想.下面让我们一起再来跟随历史的步伐,感受一种神奇的验证勾股定理的方法. 动手操作,合作拼图,小组探究. 动笔从不同的角度,计算图形的面积. 继续动手操作,合作拼图,小组探究. 继续动笔从不同的角度,计算图形的面积. 拼图活动,引发了学生的猜想,增加了研究的趣味性,锻炼了学生的空间思维能力和动手能力. 在毕达哥拉斯“两图”证明简化为“一图”证明.通过学生相互讨论使学生主动参与到学习活动中来,感悟数与形的完美结合,同时感悟勾股定理所蕴含的数学文化. 在邹元治和赵爽证法“一图”证明的基础上再次简化为“半图”证明.
(四)追溯历史 丰富认识 活动四:如何把两个正方形纸片通过裁剪拼成一个正方形? (几何画板展示)两个正方形的面积正好为a2+b2,因此,将这两个正方形剪裁拼成一个边长为多少的正方形就可以验证勾股定理了?(边长为c)图中有没有隐含了长度为c的线段呢?你能找出来吗?正方形如何画?所构造出来的正方形外面的部分如何已入到内部呢? 这种验证勾股定理的方法是我国古代著名的数学家刘徽给出.因为所涉及到两个的正方形的颜色为青色和红色,把这个图形形象地成为“青朱出入图”.这种验证方法无须著一字,让人们对于勾股定理心领神会.因此,也称这种方法为“无字证明”. 积极思考,代表回答. 通过问题串,提高学生的观察分析能力,培养学生善于思考的良好习惯.
(五)课堂练习 应用新知 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的"面积法"给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1摆放时,都可以用"面积法"来证明,请你帮助小聪. 求证:a2+b2=c2 变式:当两个全等的直角三角形如图2摆放时,请你帮助小聪利用图2,求证:a2+b2=c2 动笔计算,小组讨论 再次让学生感悟到对于同一个对象从不同的角度加以研究,常常可以发现新的结论.
(六)总结反思 提炼精华 谈谈通过本节课的学习,你有哪些收获和感悟呢? 讨论后共同小结. 师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力.
(七)课后作业 拓展延伸 课后上网搜集更多的勾股定理的验证方法,和同学交流讨论. 课后交流讨论. 拓宽视角,提升兴趣.
教学目标 1.让学生经历验证探索勾股定理的过程,培养学生主动探究意识,发展合情推理的能力,体会数形结合思想. 2.经历用多种拼图方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考与表达的能力,感受勾股定理蕴含的数学文化和丰富的数学思想.
教学重点 通过综合运用已有知识解决问题的过程,加深对数形结合的思想的认识.
教学难点 通过拼图验证勾股定理的过程,使学生获得一些研究问题与合作交流的方法与经验.
教学过程(教师) 学生活动 设计思路
(一)创设情境 提出问题 同学们,上一节可我们学习了著名的数学定理——《勾股定理》.大家还记得勾股定理的内容是什么吗?它用符号语言又可以如何表示呢? 上一节课,我们主要通过观察、测量、猜想得到了勾股定理.我们知道仅仅靠观察、测量、猜想并不严谨.因此,本节课我们一起来验证勾股定理. 复习回顾,兴趣盎然. 这是对上一节课勾股定理内容的回顾,从学生的原有认知出发,揭示这节课产生的根源,符合学生的认知心理,也自然地引出本节课的目标.
(二)旧知回顾 经验迁移 七年级时我们曾经通过计算一些图形的面积,得到了数学公式,大家还记得在哪用过吗? (学生讨论) 课件展示:平方差公式、完全平方公式、单项式乘多项式、多项式乘多项式. (a+b)(a-b)=a2-b2 (a+b)2=a2+2ab+b2 a(b+c+d)=ab+ac+ad (a+b)(c+d)=ac+ad+bc+bd 今天,我们也来利用这些经验尝试计算一些图形的面积来验证勾股定理. 积极思考,回答问题. 从学生已有认知出发,将验证勾股定理的问题转化为探究一些图形的面积的问题
(三)实践探索 合作探究 1.活动准备:揭下《数学实验手册》附录4的8个完全相同的直角三角形和1号、2号、3号正方形纸片. (不妨设两直角边分别为a、b ,且a≤b ,斜边为 c) 2. 活动一: 选用4个完全相同的直角三角形和1 号正方形纸片,拼成1个新的正方形; 选用4个完全相同的直角三角形和2 号、3号正方形纸片,拼成1个新的正方形; (3) 你能利用所拼成的2个正方形证明验证勾股定理吗? 其实,再来观察这两幅图形,两幅图形都是边长为a+b的正方形,面积相等.减去里面四个完全相同的直角三角形,剩余的部分面积也应该相等.而第一幅图形中剩余部分是正方形,边长为c,因此剩余部分面积为c2,第二幅图形中剩余部分为两个边长分别为a,b的正方形,面积和为a2+b2.这样可以不用动笔计算,直接得到勾股定理. 这是勾股定理最早的证明,它是著名的毕达哥拉斯学派的贡献,因此这种证明勾股定理的方法叫做“毕达哥拉斯证法”.这种证法不仅最早,而且也是最直观的图形验证的方法,它可以不用图形之外的语言让我们看明白勾股定理的正确性. 然而,这种证明勾股定理的方法弊端是图形涉及两个正方形,图形构造不容易想到. 3.活动二: 你能只利用这一个图形验证勾股定理吗? 这种证明勾股定理的方法是我国数学家邹元治的证法,只用了毕达哥拉斯证法中的一个图形,就验证了勾股定理. 邹元治证法涉及的图形,也可以理解为用四个完全相同的直角三角形拼成了边长为c的正方形. 你还能只利用4个完全相同的直角三角形拼成边长为c的正方形验证勾股定理吗? 这个图案是我国古代著名的数学家赵爽在注解《周髀算经》时所给出.因此人们为了纪念赵爽,将这副图案叫做赵爽弦图.这也是我国对于勾股定理的第一个证明,代表了我国古代数学的成就. 正因为如此,2002年世界数学家大会,正是以赵爽弦图为大会的会徽.它也像是一个转动的风车,欢迎全世界各国的数学家到我国进行思想的交流和智慧的碰撞. 以上活动中的验证方法至少涉及四个直角三角形,能否再简化证明的图形呢? 活动三: 你能只利用2个完全相同的直角三角形所拼 成的图形验证勾股定理吗? 这种证明勾股定理的方法是美国第二十届总统伽菲尔德的证法,人们为了纪念伽菲尔德,将这种证明勾股定理的方法,叫做总统证法.总统证法相比前面的验证方法,图形更加的简洁,明了. 其实,从古至今,人们对验证勾股定理的方法不断地探索创新,产生了许多的奇思妙想.下面让我们一起再来跟随历史的步伐,感受一种神奇的验证勾股定理的方法. 动手操作,合作拼图,小组探究. 动笔从不同的角度,计算图形的面积. 继续动手操作,合作拼图,小组探究. 继续动笔从不同的角度,计算图形的面积. 拼图活动,引发了学生的猜想,增加了研究的趣味性,锻炼了学生的空间思维能力和动手能力. 在毕达哥拉斯“两图”证明简化为“一图”证明.通过学生相互讨论使学生主动参与到学习活动中来,感悟数与形的完美结合,同时感悟勾股定理所蕴含的数学文化. 在邹元治和赵爽证法“一图”证明的基础上再次简化为“半图”证明.
(四)追溯历史 丰富认识 活动四:如何把两个正方形纸片通过裁剪拼成一个正方形? (几何画板展示)两个正方形的面积正好为a2+b2,因此,将这两个正方形剪裁拼成一个边长为多少的正方形就可以验证勾股定理了?(边长为c)图中有没有隐含了长度为c的线段呢?你能找出来吗?正方形如何画?所构造出来的正方形外面的部分如何已入到内部呢? 这种验证勾股定理的方法是我国古代著名的数学家刘徽给出.因为所涉及到两个的正方形的颜色为青色和红色,把这个图形形象地成为“青朱出入图”.这种验证方法无须著一字,让人们对于勾股定理心领神会.因此,也称这种方法为“无字证明”. 积极思考,代表回答. 通过问题串,提高学生的观察分析能力,培养学生善于思考的良好习惯.
(五)课堂练习 应用新知 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的"面积法"给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1摆放时,都可以用"面积法"来证明,请你帮助小聪. 求证:a2+b2=c2 变式:当两个全等的直角三角形如图2摆放时,请你帮助小聪利用图2,求证:a2+b2=c2 动笔计算,小组讨论 再次让学生感悟到对于同一个对象从不同的角度加以研究,常常可以发现新的结论.
(六)总结反思 提炼精华 谈谈通过本节课的学习,你有哪些收获和感悟呢? 讨论后共同小结. 师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力.
(七)课后作业 拓展延伸 课后上网搜集更多的勾股定理的验证方法,和同学交流讨论. 课后交流讨论. 拓宽视角,提升兴趣.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
