1.3 第一课时 并集和交集(共40张PPT)
文档属性
| 名称 | 1.3 第一课时 并集和交集(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 21:26:25 | ||
图片预览








文档简介
(共40张PPT)
1.3 集合的基本运算
第一课时 并集和交集
明学习目标 知结构体系
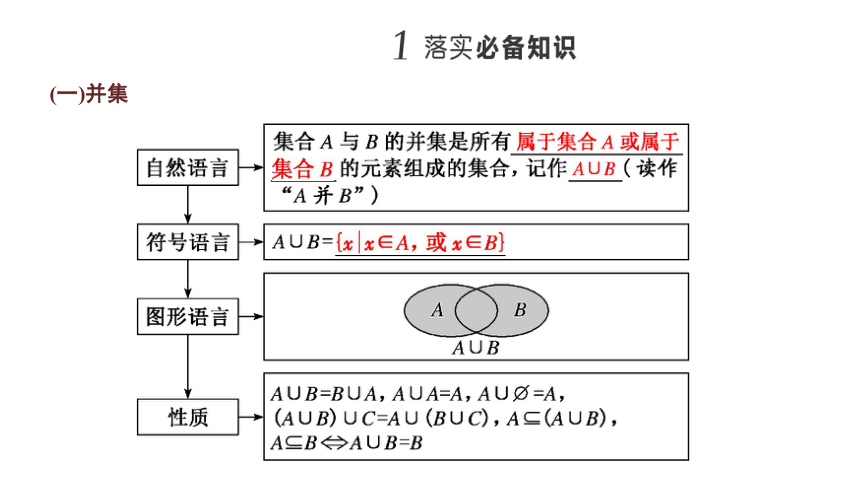
课标 要求 1.理解两个集合的并集的含义. 2.理解两个集合的交集的含义. 3.理解并集、交集的基本性质,会求两个集合的并集与交集. 4.能使用Venn图表达集合的交集与并集.
重点 难点 重点:集合的并集与交集运算. 难点:利用运算的性质求参数. (一)并集
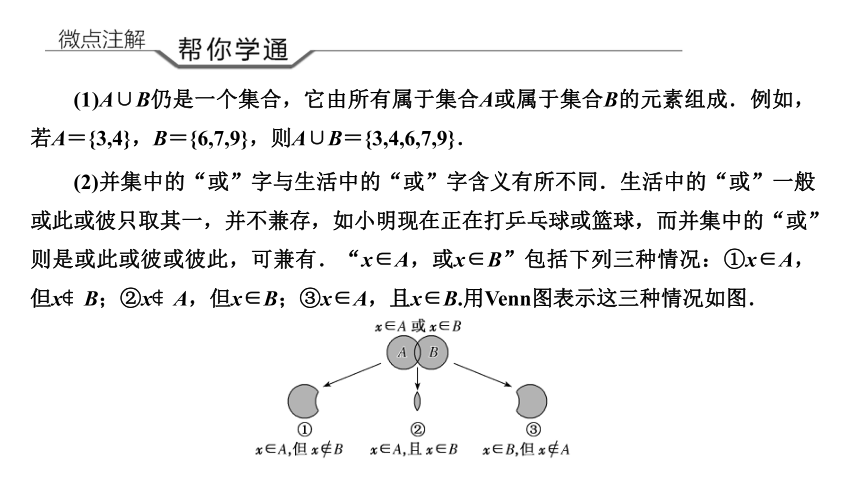
(1)A∪B仍是一个集合,它由所有属于集合A或属于集合B的元素组成.例如,若A={3,4},B={6,7,9},则A∪B={3,4,6,7,9}.
(2)并集中的“或”字与生活中的“或”字含义有所不同.生活中的“或”一般或此或彼只取其一,并不兼存,如小明现在正在打乒乓球或篮球,而并集中的“或”则是或此或彼或彼此,可兼有.“x∈A,或x∈B”包括下列三种情况:①x∈A,但x B;②x A,但x∈B;③x∈A,且x∈B.用Venn图表示这三种情况如图.
(3)因为集合中的元素具有互异性,所以集合A和B的公共元素在并集中只能出现一次,如A={1,2,3},B={1,2},则A∪B={1,2,3},而不能写成A∪B={1,1,2,2,3},因此不能简单地认为A∪B是由A的所有元素和B的所有元素并在一起组成的集合.
[即时小练]
1.若集合M={-1,0},N={0,1},则M∪N=________.
解析:M∪N表示属于M或属于N的元素构成的集合,故M∪N={-1,0,1}.
答案:{-1,0,1}
2.已知集合A={x|x>0},B={x|1≤x≤2},则A∪B=________.
解析:A∪B={x|x>0}∪{x|1≤x≤2}={x|x>0}.
答案:{x|x>0}
(二)交集
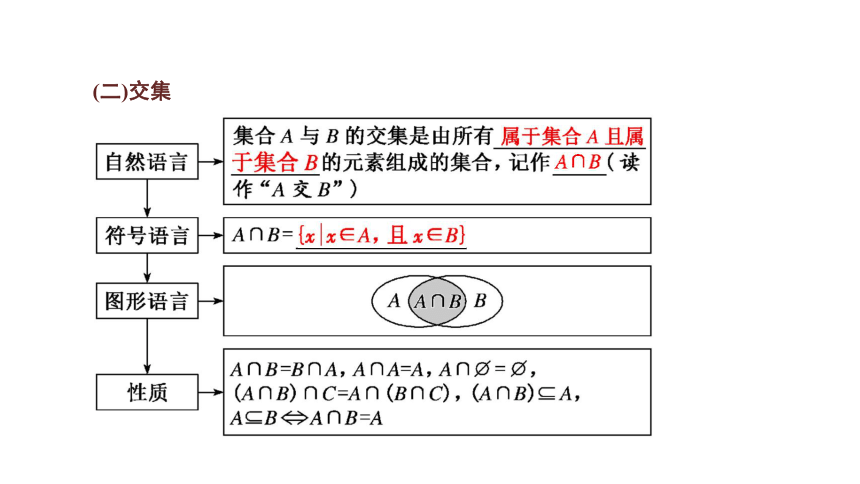
(1)交集概念中的“且”即“同时”的意思,两个集合交集中的元素必须同时是两个集合中的元素.
(2)交集概念中的“所有”两字不能省略,否则将会漏掉一些元素,一定要将相同的元素全部找出来.如A={1,2,3,4},B={2,3,4,5},则A∩B={2,3,4},而不是{2,3},{2,4}或{3,4}.
(3)集合A与B没有公共元素,不能说两个集合没有交集,而是A∩B= .例如:A={x|y=2x+3},B={(x,y)|y=x2+3},则A∩B= .原因是A为数集,B为点集,两者不可能有公共元素,故A∩B= .
[即时小练]
1.设集合M={0,1,2},N={1,2,3},则M∩N=________,M∪N=________.
解析:∵M={0,1,2},N={1,2,3},∴M∩N={1,2},M∪N={0,1,2,3}.
答案:{1,2} {0,1,2,3}
2.已知集合A={x|1解析:因为A={x|1答案:{x|1[题点一]
并 集
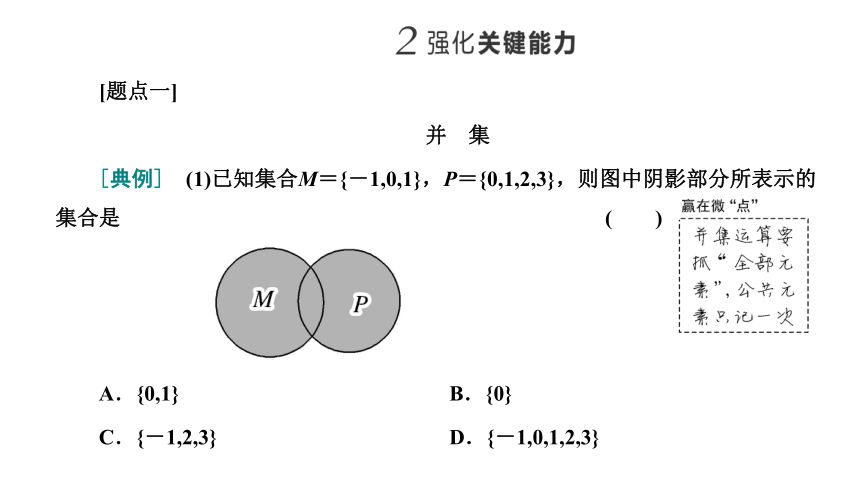
[典例] (1)已知集合M={-1,0,1},P={0,1,2,3},则图中阴影部分所表示的集合是 ( )
A.{0,1} B.{0}
C.{-1,2,3} D.{-1,0,1,2,3}
(2)设集合A={x|-1A.{x|-1C.{x|1[解析] (1)由Venn图,可知阴影部分所表示的集合是M∪P.因为M={-1,0,1},P={0,1,2,3},
故M∪P={-1,0,1,2,3}.
(2)在数轴上表示出A,B,如图所示.
由图知A∪B={x|-1[答案] (1)D (2)A
[方法技巧]
求两个集合的并集的方法
(1)对于元素个数有限的集合,可直接根据集合的并集定义求解,但要注意集合中元素的互异性.
(2)对于元素个数无限的集合,进行并集运算时,可借助数轴求解.注意两个集合的并集等于两个集合在数轴上的相应图形所覆盖的全部范围,建立不等式时,要注意端点值是否能取到,最好是把端点值代入题目验证.
[对点训练]
1.已知集合A={1,2},集合B满足A∪B={1,2,3},则满足条件的集合B有 ( )
A.2个 B.3个
C.4个 D.1个
解析:因为集合A={1,2},
集合B满足A∪B={1,2,3},
所以集合B={3},{1,3},{2,3},{1,2,3}.
答案:C
2.若集合M={x|-35},则M∪N= ( )
A.{x|x<-3或x>5} B.{x|-5C.{x|-3-3}
解析:因为M={x|-3N={x|x<-5或x>5},
所以M∪N={x|x<-5或x>-3},故选D.
答案:D
[题点二]
交 集
[典例] (1)已知集合A={x∈N|1≤x≤9},B={x|0A.{2,3,4} B.{1,2,3,4}
C.{x|1≤x≤5} D.{x|1≤x<5}
(2)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于 ( )
A.{x|0≤x≤2} B.{x|1≤x≤2}
C.{x|0≤x≤4} D.{x|1≤x≤4}
[解析] (1)由题意,集合A={x∈N|1≤x≤9}={1,2,3,4,5,6,7,8,9},B={x|0则A∩B={1,2,3,4}.
(2)在数轴上表示出集合A与B,如图所示.
则由交集的定义,知A∩B={x|0≤x≤2}.
[答案] (1)B (2)A
[方法技巧]
求两个集合的交集的方法
(1)对于元素个数有限的集合,可逐个挑出两个集合的相同元素,但要注意集合中元素的互异性.
(2)对于元素个数无限的集合,可借助数轴求交集,两集合的交集对应的是表示两集合的相应图形所覆盖的公共区域.
[对点训练]
1.已知集合A={1,2,3,4},B={2,4,6},则图中阴影部分表示的集合为 ( )
A.{2,4} B.{2,6}
C.{2,4,6} D.{1,2,3,4}
解析:图中阴影部分表示的集合为A∩B={2,4},故选A.
答案:A
2.已知集合A={x|x=3n-1,n∈N},B={6,8,10,12,14},则集合A∩B中元素的个数为 ( )
A.5 B.4
C.3 D.2
解析:求x=3n-1=6,8,10,12,14的整数解,易知x=3n-1=8,14有整数解,此时n=3,5,所以A∩B={8,14}有2个元素,故选D.
答案:D
3.(2021·全国乙卷)已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T= ( )
A. B.S
C.T D.Z
解析:集合S是由奇数组成的集合,集合T是由被4除余1的整数组成的集合,所以T S,则S∩T=T.故选C.
答案:C
[题点三]
根据并集、交集运算求参数
[典例] 已知集合A={x|-3<x≤4},集合B={x|k+1≤x≤2k-1},
且A∪B=A,试求实数k的取值范围.
[方法技巧]
利用集合的运算结果求参数问题的解题思路
对于已知集合的运算结果求参数值或范围的问题,一般先观察得到不同集合中元素之间的关系,再列方程(组)或不等式(组)求解.在处理有关含参数的集合问题时,要注意对求解结果进行检验.
答案:D
2.已知集合A={x|x2-3x+2=0},B={x|mx-1=0},若A∪B=A,则实数m构成的集合为________.
一、在典题训练中内化学科素养
本节突出对数学语言的理解,数学运算、逻辑推理素养的考查,常与函数方程、不等式等知识综合,提升学生分析问题、解决综合问题的能力.
1.(2020·新高考全国卷Ⅱ)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B=( )
A.{1,8} B.{2,5}
C.{2,3,5} D.{1,2,3,5,8}
答案:C
2.(2020·新高考全国卷Ⅰ)设集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|1解析:A={x|1≤x≤3},B={x|2则A∪B={x|1≤x<4},故选C.
答案:C
3.(2021·新高考Ⅰ卷)设集合A={x|-2<x<4},B={2,3,4,5},则A∩B= ( )
A.{2} B.{2,3}
C.{3,4} D.{2,3,4}
解析:因为A={x|-2<x<4},
B={2,3,4,5},
所以A∩B={2,3}.故选B.
答案:B
4.(2020·全国卷Ⅰ)设集合A={x|x2-4≤0},B={x|2x+a≤0},且A∩B={x|-2≤x≤1},则a= ( )
A.-4 B.-2
C.2 D.4
答案:B
内化素养
数学 运算 考查集合的并集运算与交集运算,连续的数集运算注意端点值的取舍
逻辑 推理 利用集合的交、并集进行逆向求参,逻辑推理求出参数的值
5.(2020·新高考全国卷Ⅰ)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是 ( )
A.62% B.56%
C.46% D.42%
解析: 设集合A为喜欢足球的学生,B为喜欢游泳的学生,如
图所示.故既喜欢足球又喜欢游泳的学生总数占该校学生总
数的比例是60%+82%-96%=46%.
答案:C
内化素养
数学建模 用集合表示有关实际问题,并利用集合知识来分析、解决问题
直观想象 利用Venn图的形象直观分析解决问题
二、在导向训练中品悟核心价值
?发展理性思维
1.已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为 ( )
A.3 B.2
C.1 D.0
解析:因为A表示圆x2+y2=1上的点的集合,B表示直线y=x上的点的集合,直线y=x与圆x2+y2=1有两个交点,所以A∩B中元素的个数为2.
答案:B
2.满足M {a1,a2,a3,a4},且M∩{a1,a2,a3}={a1,a2}的集合M的个数是( )
A.1 B.2
C.3 D.4
解析:由题意知集合M一定含有元素a1,a2,并且不含元素a3,故M={a1,a2}或M={a1,a2,a4}.
答案:B
?体察数学文化
3.中国古代重要的数学著作《孙子算经》下卷有题:今有物,不知其数.三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何?现有如下表示:已知A={x|x=3n+2,n∈N*},B={x|x=5n+3,n∈N*},C={x|x=7n+2,n∈N*},若x∈A∩B∩C,则下列选项中符合题意的整数x为 ( )
A.8 B.127
C.37 D.23
解析:因为8=7×1+1,则8 C,选项A错误;
127=3×42+1,则127 A,选项B错误;
37=3×12+1,则37 A,选项C错误;
23=3×7+2,故23∈A;23=5×4+3,故23∈B;23=7×3+2,故23∈C,则23∈A∩B∩C,选项D正确.
答案:D
4. 集合论是德国数学家康托尔(G.Cantor)于19世纪末创立的.在他的集合理论中,用card(A)表示有限集合中元素的个数,例如:A={a,b,c},则card(A)=3.若对于任意两个有限集合A,B,有card(A∪B)=card(A)+card(B)-card(A∩B).某校举办运动会,高一(1)班参加田赛的学生有14人,参加径赛的学生有9人,两项都参加的有5人,那么高一(1)班参加本次运动会的人数共有 ( )
A.28 B.23
C.18 D.16
解析:设参加田赛的学生组成集合A,则card(A)=14,参加径赛的学生组成集合B,则card(B)=9,由题意得card(A∩B)=5,
所以card(A∪B)=card(A)+card(B)-card(A∩B)=14+9-5=18,
所以高一(1)班参加本次运动会的人数共有18.
答案:C
?强化拓广探索
5.设M,P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)= ( )
A.M∩P B.M∪P
C.M D.P
解析:由新定义知M-(M-P)表示由属于M且属于P的所有元素构成的集合,即集合M∩P.故选A.
答案:A
答案:C
1.3 集合的基本运算
第一课时 并集和交集
明学习目标 知结构体系
课标 要求 1.理解两个集合的并集的含义. 2.理解两个集合的交集的含义. 3.理解并集、交集的基本性质,会求两个集合的并集与交集. 4.能使用Venn图表达集合的交集与并集.
重点 难点 重点:集合的并集与交集运算. 难点:利用运算的性质求参数. (一)并集
(1)A∪B仍是一个集合,它由所有属于集合A或属于集合B的元素组成.例如,若A={3,4},B={6,7,9},则A∪B={3,4,6,7,9}.
(2)并集中的“或”字与生活中的“或”字含义有所不同.生活中的“或”一般或此或彼只取其一,并不兼存,如小明现在正在打乒乓球或篮球,而并集中的“或”则是或此或彼或彼此,可兼有.“x∈A,或x∈B”包括下列三种情况:①x∈A,但x B;②x A,但x∈B;③x∈A,且x∈B.用Venn图表示这三种情况如图.
(3)因为集合中的元素具有互异性,所以集合A和B的公共元素在并集中只能出现一次,如A={1,2,3},B={1,2},则A∪B={1,2,3},而不能写成A∪B={1,1,2,2,3},因此不能简单地认为A∪B是由A的所有元素和B的所有元素并在一起组成的集合.
[即时小练]
1.若集合M={-1,0},N={0,1},则M∪N=________.
解析:M∪N表示属于M或属于N的元素构成的集合,故M∪N={-1,0,1}.
答案:{-1,0,1}
2.已知集合A={x|x>0},B={x|1≤x≤2},则A∪B=________.
解析:A∪B={x|x>0}∪{x|1≤x≤2}={x|x>0}.
答案:{x|x>0}
(二)交集
(1)交集概念中的“且”即“同时”的意思,两个集合交集中的元素必须同时是两个集合中的元素.
(2)交集概念中的“所有”两字不能省略,否则将会漏掉一些元素,一定要将相同的元素全部找出来.如A={1,2,3,4},B={2,3,4,5},则A∩B={2,3,4},而不是{2,3},{2,4}或{3,4}.
(3)集合A与B没有公共元素,不能说两个集合没有交集,而是A∩B= .例如:A={x|y=2x+3},B={(x,y)|y=x2+3},则A∩B= .原因是A为数集,B为点集,两者不可能有公共元素,故A∩B= .
[即时小练]
1.设集合M={0,1,2},N={1,2,3},则M∩N=________,M∪N=________.
解析:∵M={0,1,2},N={1,2,3},∴M∩N={1,2},M∪N={0,1,2,3}.
答案:{1,2} {0,1,2,3}
2.已知集合A={x|1
并 集
[典例] (1)已知集合M={-1,0,1},P={0,1,2,3},则图中阴影部分所表示的集合是 ( )
A.{0,1} B.{0}
C.{-1,2,3} D.{-1,0,1,2,3}
(2)设集合A={x|-1
故M∪P={-1,0,1,2,3}.
(2)在数轴上表示出A,B,如图所示.
由图知A∪B={x|-1
[方法技巧]
求两个集合的并集的方法
(1)对于元素个数有限的集合,可直接根据集合的并集定义求解,但要注意集合中元素的互异性.
(2)对于元素个数无限的集合,进行并集运算时,可借助数轴求解.注意两个集合的并集等于两个集合在数轴上的相应图形所覆盖的全部范围,建立不等式时,要注意端点值是否能取到,最好是把端点值代入题目验证.
[对点训练]
1.已知集合A={1,2},集合B满足A∪B={1,2,3},则满足条件的集合B有 ( )
A.2个 B.3个
C.4个 D.1个
解析:因为集合A={1,2},
集合B满足A∪B={1,2,3},
所以集合B={3},{1,3},{2,3},{1,2,3}.
答案:C
2.若集合M={x|-3
A.{x|x<-3或x>5} B.{x|-5
解析:因为M={x|-3
所以M∪N={x|x<-5或x>-3},故选D.
答案:D
[题点二]
交 集
[典例] (1)已知集合A={x∈N|1≤x≤9},B={x|0
C.{x|1≤x≤5} D.{x|1≤x<5}
(2)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于 ( )
A.{x|0≤x≤2} B.{x|1≤x≤2}
C.{x|0≤x≤4} D.{x|1≤x≤4}
[解析] (1)由题意,集合A={x∈N|1≤x≤9}={1,2,3,4,5,6,7,8,9},B={x|0
(2)在数轴上表示出集合A与B,如图所示.
则由交集的定义,知A∩B={x|0≤x≤2}.
[答案] (1)B (2)A
[方法技巧]
求两个集合的交集的方法
(1)对于元素个数有限的集合,可逐个挑出两个集合的相同元素,但要注意集合中元素的互异性.
(2)对于元素个数无限的集合,可借助数轴求交集,两集合的交集对应的是表示两集合的相应图形所覆盖的公共区域.
[对点训练]
1.已知集合A={1,2,3,4},B={2,4,6},则图中阴影部分表示的集合为 ( )
A.{2,4} B.{2,6}
C.{2,4,6} D.{1,2,3,4}
解析:图中阴影部分表示的集合为A∩B={2,4},故选A.
答案:A
2.已知集合A={x|x=3n-1,n∈N},B={6,8,10,12,14},则集合A∩B中元素的个数为 ( )
A.5 B.4
C.3 D.2
解析:求x=3n-1=6,8,10,12,14的整数解,易知x=3n-1=8,14有整数解,此时n=3,5,所以A∩B={8,14}有2个元素,故选D.
答案:D
3.(2021·全国乙卷)已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T= ( )
A. B.S
C.T D.Z
解析:集合S是由奇数组成的集合,集合T是由被4除余1的整数组成的集合,所以T S,则S∩T=T.故选C.
答案:C
[题点三]
根据并集、交集运算求参数
[典例] 已知集合A={x|-3<x≤4},集合B={x|k+1≤x≤2k-1},
且A∪B=A,试求实数k的取值范围.
[方法技巧]
利用集合的运算结果求参数问题的解题思路
对于已知集合的运算结果求参数值或范围的问题,一般先观察得到不同集合中元素之间的关系,再列方程(组)或不等式(组)求解.在处理有关含参数的集合问题时,要注意对求解结果进行检验.
答案:D
2.已知集合A={x|x2-3x+2=0},B={x|mx-1=0},若A∪B=A,则实数m构成的集合为________.
一、在典题训练中内化学科素养
本节突出对数学语言的理解,数学运算、逻辑推理素养的考查,常与函数方程、不等式等知识综合,提升学生分析问题、解决综合问题的能力.
1.(2020·新高考全国卷Ⅱ)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B=( )
A.{1,8} B.{2,5}
C.{2,3,5} D.{1,2,3,5,8}
答案:C
2.(2020·新高考全国卷Ⅰ)设集合A={x|1≤x≤3},B={x|2
答案:C
3.(2021·新高考Ⅰ卷)设集合A={x|-2<x<4},B={2,3,4,5},则A∩B= ( )
A.{2} B.{2,3}
C.{3,4} D.{2,3,4}
解析:因为A={x|-2<x<4},
B={2,3,4,5},
所以A∩B={2,3}.故选B.
答案:B
4.(2020·全国卷Ⅰ)设集合A={x|x2-4≤0},B={x|2x+a≤0},且A∩B={x|-2≤x≤1},则a= ( )
A.-4 B.-2
C.2 D.4
答案:B
内化素养
数学 运算 考查集合的并集运算与交集运算,连续的数集运算注意端点值的取舍
逻辑 推理 利用集合的交、并集进行逆向求参,逻辑推理求出参数的值
5.(2020·新高考全国卷Ⅰ)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是 ( )
A.62% B.56%
C.46% D.42%
解析: 设集合A为喜欢足球的学生,B为喜欢游泳的学生,如
图所示.故既喜欢足球又喜欢游泳的学生总数占该校学生总
数的比例是60%+82%-96%=46%.
答案:C
内化素养
数学建模 用集合表示有关实际问题,并利用集合知识来分析、解决问题
直观想象 利用Venn图的形象直观分析解决问题
二、在导向训练中品悟核心价值
?发展理性思维
1.已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为 ( )
A.3 B.2
C.1 D.0
解析:因为A表示圆x2+y2=1上的点的集合,B表示直线y=x上的点的集合,直线y=x与圆x2+y2=1有两个交点,所以A∩B中元素的个数为2.
答案:B
2.满足M {a1,a2,a3,a4},且M∩{a1,a2,a3}={a1,a2}的集合M的个数是( )
A.1 B.2
C.3 D.4
解析:由题意知集合M一定含有元素a1,a2,并且不含元素a3,故M={a1,a2}或M={a1,a2,a4}.
答案:B
?体察数学文化
3.中国古代重要的数学著作《孙子算经》下卷有题:今有物,不知其数.三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何?现有如下表示:已知A={x|x=3n+2,n∈N*},B={x|x=5n+3,n∈N*},C={x|x=7n+2,n∈N*},若x∈A∩B∩C,则下列选项中符合题意的整数x为 ( )
A.8 B.127
C.37 D.23
解析:因为8=7×1+1,则8 C,选项A错误;
127=3×42+1,则127 A,选项B错误;
37=3×12+1,则37 A,选项C错误;
23=3×7+2,故23∈A;23=5×4+3,故23∈B;23=7×3+2,故23∈C,则23∈A∩B∩C,选项D正确.
答案:D
4. 集合论是德国数学家康托尔(G.Cantor)于19世纪末创立的.在他的集合理论中,用card(A)表示有限集合中元素的个数,例如:A={a,b,c},则card(A)=3.若对于任意两个有限集合A,B,有card(A∪B)=card(A)+card(B)-card(A∩B).某校举办运动会,高一(1)班参加田赛的学生有14人,参加径赛的学生有9人,两项都参加的有5人,那么高一(1)班参加本次运动会的人数共有 ( )
A.28 B.23
C.18 D.16
解析:设参加田赛的学生组成集合A,则card(A)=14,参加径赛的学生组成集合B,则card(B)=9,由题意得card(A∩B)=5,
所以card(A∪B)=card(A)+card(B)-card(A∩B)=14+9-5=18,
所以高一(1)班参加本次运动会的人数共有18.
答案:C
?强化拓广探索
5.设M,P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x P},则M-(M-P)= ( )
A.M∩P B.M∪P
C.M D.P
解析:由新定义知M-(M-P)表示由属于M且属于P的所有元素构成的集合,即集合M∩P.故选A.
答案:A
答案:C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
