1.5.2 全称量词命题与存在量词命题的否定(共29张PPT)
文档属性
| 名称 | 1.5.2 全称量词命题与存在量词命题的否定(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 21:28:44 | ||
图片预览








文档简介
(共29张PPT)
1.5.2 全称量词命题与存在量词命题的否定
明学习目标 知结构体系
课标 要求 1.能正确使用存在量词对全称量词命题进行否定. 2.能正确使用全称量词对存在量词命题进行否定.
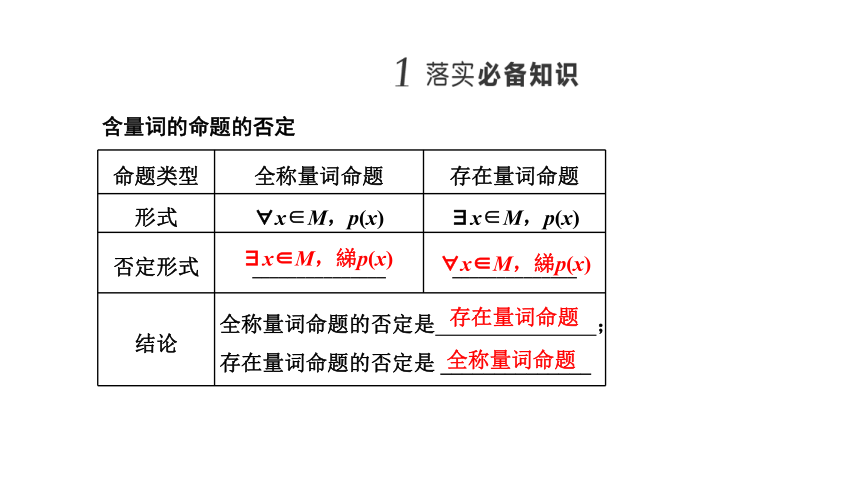
重点 难点 重点:全称量词命题与存在量词命题的否定. 难点:根据全称量词命题与存在量词命题求参数. 含量词的命题的否定
命题类型 全称量词命题 存在量词命题
形式 x∈M,p(x) x∈M,p(x)
否定形式 _______________ ______________
结论 全称量词命题的否定是 ; 存在量词命题的否定是 ______________ x∈M,綈p(x)
x∈M,綈p(x)
存在量词命题
全称量词命题
1.对含量词的命题的否定的理解
(1)要否定全称量词命题“ x∈M,p(x)”,只需在M中找到一个x,使得p(x)不成立,也就是命题“ x∈M,綈p(x)”成立;
(2)要否定存在量词命题“ x∈M,p(x)”,需要验证对M中的每一个x,均有p(x)不成立,也就是命题“ x∈M,綈p(x)”成立.
即在书写这两种命题的否定时,要将相应的存在量词变为全称量词,全称量词变为存在量词.
2.否定一个含有量词的命题的三点注意
(1)弄清命题是全称量词命题还是存在量词命题,是正确写出命题否定的关键;
(2)注意命题的否定与否命题的区别;
(3)当命题否定的真假不易判断时,可以转化为去判断原命题的真假,当原命题为真时,命题的否定为假,当原命题为假时,命题的否定为真.
[即时小练]
1.命题“ x∈R,|x|+x2≥0”的否定是 ( )
A. x∈R,|x|+x2<0
B. x∈R,|x|+x2≤0
C. x∈R,|x|+x2<0
D. x∈R,|x|+x2≥0
解析:此全称量词命题的否定为 x∈R,|x|+x2<0.
答案:C
2.命题“ x>0,2x2=5x-1”的否定是 ( )
A. x>0,2x2≠5x-1
B. x≤0,2x2=5x-1
C. x>0,2x2≠5x-1
D. x≤0,2x2=5x-1
解析:存在量词命题的否定是全称量词命题.
答案:A
3.命题:“有的三角形是直角三角形”的否定是:____________________.
解析:命题:“有的三角形是直角三角形”是存在量词命题,其否定是全称量词命题,即所有的三角形都不是直角三角形.
答案:所有的三角形都不是直角三角形
[题点一]
全称量词命题的否定
[典例] 写出下列全称量词命题的否定:
(1)所有自然数的平方都是正数;
(2)任何实数x都是方程5x-12=0的根;
(3)对任意实数x,x2+1≥0.
[方法技巧]
全称量词命题否定的关注点
(1)全称量词命题p: x∈M,p(x),它的否定: x∈M,綈p(x).
(2)全称量词命题的否定是存在量词命题,对省略全称量词的全称量词命题可补上量词后再进行否定.
[对点训练]
1.命题“ x∈R,x2-x+1=0”的否定为 ( )
A. x∈R,x2-x+1≠0 B. x∈R,x2-x+1=0
C. x∈R,x2-x+1≠0 D. x R,x2-x+1≠0
解析:根据全称量词命题的否定是存在量词命题,所以“ x∈R,x2-x+1=0”的否定为 “ x∈R,x2-x+1≠0”.
答案:C
2.命题“对任意的x∈R,x3-2x+1≤0”的否定是 ( )
A.不存在x∈R,x3-2x+1≤0
B.存在x∈R,x3-2x+1≤0
C.存在x∈R,x3-2x+1>0
D.对任意的x∈R,x3-2x+1>0
解析:命题“对任意的x∈R,x3-2x+1≤0”的否定是“存在x∈R,x3-2x+1>0”.
答案:C
[方法技巧]
存在量词命题否定的关注点
(1)存在量词命题的否定是全称量词命题,写命题的否定时要分别改变其中的量词和判断词.即p: x∈M,p(x),它的否定: x∈M,綈p(x).
(2)存在量词命题的否定是全称量词命题,对省略存在量词的存在量词命题可补上量词后进行否定.
[对点训练]
1.命题“存在x∈R,使得x2+2x<1”的否定是 ( )
A.对任意x∈R,都有x2+2x>1
B.对任意x∈R,都有x2+2x≥1
C.存在x∈R,使得x2+2x>1
D.存在x∈R,使得x2+2x≥1
解析:命题“存在x∈R,使得x2+2x<1”为存在量词命题,该命题的否定为对任意x∈R,都有x2+2x≥1.
答案:B
答案:D
[方法技巧]
解决含有量词的命题求参问题的思路
(1)全称量词命题求参的问题,常以一次函数、二次函数等为载体进行考查,一般在题目中会出现“恒成立”等词语.解决此类问题时,可构造函数,利用数形结合求参数范围,也可用分离参数法求参数范围.
(2)存在量词命题求参数范围的问题中常出现“存在”等词语,对于此类问题,通常是假设存在满足条件的参数,然后利用条件求参数范围,若能求出参数范围,则假设成立;否则,假设不成立.解决有关存在量词命题的参数的取值范围问题时,应尽量分离参数.
一、在典题训练中内化学科素养
本节考查的重点是两种命题的否定及其真假判断,一般与其他知识相综合,同时考查逻辑推理和数学运算的核心素养.
1.设命题p: n∈N,n2>2n,则綈p为 ( )
A. n∈N,n2>2n B. n∈N,n2≤2n
C. n∈N,n2≤2n D. n∈N,n2=2n
解析:将“ ”改写成“ ”,“>”改写为“≤”即可,故选C.
答案:C
2.命题“ x∈R, n∈N*,使得n≥x2”的否定形式是 ( )
A. x∈R, n∈N*,使得nB. x∈R, n∈N*,使得nC. x∈R, n∈N*,使得nD. x∈R, n∈N*,使得n解析:将“ ”改写为“ ”,“ ”改写为“ ”,再否定结论可得命题的否定为“ x∈R, n∈N*,使得n答案:D
[内化素养/逻辑推理]
掌握含量词的命题的否定格式,注意“至少”“至多”等量词的否定.
二、在导向训练中品悟核心价值
?发展理性思维
1.命题“同位角相等”的否定为______________________.
解析:全称量词命题的否定是存在量词命题,故否定为:有的同位角不相等.
答案:有的同位角不相等
2.若命题“ x∈R,x2-4x+a≠0”为假命题,则实数a的取值范围是_______.
解析:∵命题 x∈R,x2-4x+a≠0为假命题,
∴ x∈R,x2-4x+a=0是真命题,
∴方程x2-4x+a=0有实数根,则Δ=(-4)2-4a≥0,解得a≤4.
答案:{a|a≤4}
?体察数学文化
3.马克·吐温是美国著名的幽默讽刺作家,他的小说揭露和讽刺了美国社会的一些黑暗现象.他曾痛骂美国国会“有些议员是笨蛋”,因此被要求道歉,否则被控告诽谤罪.于是马克·吐温登报表示歉意并纠正道:美国国会“有些议员不是笨蛋”.请问“有些议员不是笨蛋”的否定是 ( )
A.有些议员是笨蛋 B.每个议员都是笨蛋
C.每个议员都不是笨蛋 D.有些议员不是笨蛋
解析:根据题意可得:“有些议员不是笨蛋”的否定为“每个议员都是笨蛋”.
A:“有些议员”不正确;B:正确;C:“都不是笨蛋”与“不是笨蛋”意思相近,没有否定;D:与题干一致.
答案:B
4.假设我们要否定命题“所有水生动物都用鳃呼吸”,可以这样做:
画出表示用鳃呼吸的动物的集合,并包含表示所有水生动物的集合,如图(1)所示,那么此图就表示“所有水生动物都用鳃呼吸”.
再将图(1)中水生动物的集合部分地移出用鳃呼吸的动物的集合,如图(2),那么此图就表示“并非所有水生动物用鳃呼吸”,即“一些水生动物不用鳃呼吸”,这就得到了原命题的否定.
可以看出,当我们否定一个含有全称量词的命题时,就会得到一个含有存在量词的命题.
试举出社会生活或其他学科中命题的例子,并图示命题及该命题的否定.
解:答案不唯一,举例如下:
命题:高一(3)班所有的女生都是寄宿生.
图示如下:
1.5.2 全称量词命题与存在量词命题的否定
明学习目标 知结构体系
课标 要求 1.能正确使用存在量词对全称量词命题进行否定. 2.能正确使用全称量词对存在量词命题进行否定.
重点 难点 重点:全称量词命题与存在量词命题的否定. 难点:根据全称量词命题与存在量词命题求参数. 含量词的命题的否定
命题类型 全称量词命题 存在量词命题
形式 x∈M,p(x) x∈M,p(x)
否定形式 _______________ ______________
结论 全称量词命题的否定是 ; 存在量词命题的否定是 ______________ x∈M,綈p(x)
x∈M,綈p(x)
存在量词命题
全称量词命题
1.对含量词的命题的否定的理解
(1)要否定全称量词命题“ x∈M,p(x)”,只需在M中找到一个x,使得p(x)不成立,也就是命题“ x∈M,綈p(x)”成立;
(2)要否定存在量词命题“ x∈M,p(x)”,需要验证对M中的每一个x,均有p(x)不成立,也就是命题“ x∈M,綈p(x)”成立.
即在书写这两种命题的否定时,要将相应的存在量词变为全称量词,全称量词变为存在量词.
2.否定一个含有量词的命题的三点注意
(1)弄清命题是全称量词命题还是存在量词命题,是正确写出命题否定的关键;
(2)注意命题的否定与否命题的区别;
(3)当命题否定的真假不易判断时,可以转化为去判断原命题的真假,当原命题为真时,命题的否定为假,当原命题为假时,命题的否定为真.
[即时小练]
1.命题“ x∈R,|x|+x2≥0”的否定是 ( )
A. x∈R,|x|+x2<0
B. x∈R,|x|+x2≤0
C. x∈R,|x|+x2<0
D. x∈R,|x|+x2≥0
解析:此全称量词命题的否定为 x∈R,|x|+x2<0.
答案:C
2.命题“ x>0,2x2=5x-1”的否定是 ( )
A. x>0,2x2≠5x-1
B. x≤0,2x2=5x-1
C. x>0,2x2≠5x-1
D. x≤0,2x2=5x-1
解析:存在量词命题的否定是全称量词命题.
答案:A
3.命题:“有的三角形是直角三角形”的否定是:____________________.
解析:命题:“有的三角形是直角三角形”是存在量词命题,其否定是全称量词命题,即所有的三角形都不是直角三角形.
答案:所有的三角形都不是直角三角形
[题点一]
全称量词命题的否定
[典例] 写出下列全称量词命题的否定:
(1)所有自然数的平方都是正数;
(2)任何实数x都是方程5x-12=0的根;
(3)对任意实数x,x2+1≥0.
[方法技巧]
全称量词命题否定的关注点
(1)全称量词命题p: x∈M,p(x),它的否定: x∈M,綈p(x).
(2)全称量词命题的否定是存在量词命题,对省略全称量词的全称量词命题可补上量词后再进行否定.
[对点训练]
1.命题“ x∈R,x2-x+1=0”的否定为 ( )
A. x∈R,x2-x+1≠0 B. x∈R,x2-x+1=0
C. x∈R,x2-x+1≠0 D. x R,x2-x+1≠0
解析:根据全称量词命题的否定是存在量词命题,所以“ x∈R,x2-x+1=0”的否定为 “ x∈R,x2-x+1≠0”.
答案:C
2.命题“对任意的x∈R,x3-2x+1≤0”的否定是 ( )
A.不存在x∈R,x3-2x+1≤0
B.存在x∈R,x3-2x+1≤0
C.存在x∈R,x3-2x+1>0
D.对任意的x∈R,x3-2x+1>0
解析:命题“对任意的x∈R,x3-2x+1≤0”的否定是“存在x∈R,x3-2x+1>0”.
答案:C
[方法技巧]
存在量词命题否定的关注点
(1)存在量词命题的否定是全称量词命题,写命题的否定时要分别改变其中的量词和判断词.即p: x∈M,p(x),它的否定: x∈M,綈p(x).
(2)存在量词命题的否定是全称量词命题,对省略存在量词的存在量词命题可补上量词后进行否定.
[对点训练]
1.命题“存在x∈R,使得x2+2x<1”的否定是 ( )
A.对任意x∈R,都有x2+2x>1
B.对任意x∈R,都有x2+2x≥1
C.存在x∈R,使得x2+2x>1
D.存在x∈R,使得x2+2x≥1
解析:命题“存在x∈R,使得x2+2x<1”为存在量词命题,该命题的否定为对任意x∈R,都有x2+2x≥1.
答案:B
答案:D
[方法技巧]
解决含有量词的命题求参问题的思路
(1)全称量词命题求参的问题,常以一次函数、二次函数等为载体进行考查,一般在题目中会出现“恒成立”等词语.解决此类问题时,可构造函数,利用数形结合求参数范围,也可用分离参数法求参数范围.
(2)存在量词命题求参数范围的问题中常出现“存在”等词语,对于此类问题,通常是假设存在满足条件的参数,然后利用条件求参数范围,若能求出参数范围,则假设成立;否则,假设不成立.解决有关存在量词命题的参数的取值范围问题时,应尽量分离参数.
一、在典题训练中内化学科素养
本节考查的重点是两种命题的否定及其真假判断,一般与其他知识相综合,同时考查逻辑推理和数学运算的核心素养.
1.设命题p: n∈N,n2>2n,则綈p为 ( )
A. n∈N,n2>2n B. n∈N,n2≤2n
C. n∈N,n2≤2n D. n∈N,n2=2n
解析:将“ ”改写成“ ”,“>”改写为“≤”即可,故选C.
答案:C
2.命题“ x∈R, n∈N*,使得n≥x2”的否定形式是 ( )
A. x∈R, n∈N*,使得n
[内化素养/逻辑推理]
掌握含量词的命题的否定格式,注意“至少”“至多”等量词的否定.
二、在导向训练中品悟核心价值
?发展理性思维
1.命题“同位角相等”的否定为______________________.
解析:全称量词命题的否定是存在量词命题,故否定为:有的同位角不相等.
答案:有的同位角不相等
2.若命题“ x∈R,x2-4x+a≠0”为假命题,则实数a的取值范围是_______.
解析:∵命题 x∈R,x2-4x+a≠0为假命题,
∴ x∈R,x2-4x+a=0是真命题,
∴方程x2-4x+a=0有实数根,则Δ=(-4)2-4a≥0,解得a≤4.
答案:{a|a≤4}
?体察数学文化
3.马克·吐温是美国著名的幽默讽刺作家,他的小说揭露和讽刺了美国社会的一些黑暗现象.他曾痛骂美国国会“有些议员是笨蛋”,因此被要求道歉,否则被控告诽谤罪.于是马克·吐温登报表示歉意并纠正道:美国国会“有些议员不是笨蛋”.请问“有些议员不是笨蛋”的否定是 ( )
A.有些议员是笨蛋 B.每个议员都是笨蛋
C.每个议员都不是笨蛋 D.有些议员不是笨蛋
解析:根据题意可得:“有些议员不是笨蛋”的否定为“每个议员都是笨蛋”.
A:“有些议员”不正确;B:正确;C:“都不是笨蛋”与“不是笨蛋”意思相近,没有否定;D:与题干一致.
答案:B
4.假设我们要否定命题“所有水生动物都用鳃呼吸”,可以这样做:
画出表示用鳃呼吸的动物的集合,并包含表示所有水生动物的集合,如图(1)所示,那么此图就表示“所有水生动物都用鳃呼吸”.
再将图(1)中水生动物的集合部分地移出用鳃呼吸的动物的集合,如图(2),那么此图就表示“并非所有水生动物用鳃呼吸”,即“一些水生动物不用鳃呼吸”,这就得到了原命题的否定.
可以看出,当我们否定一个含有全称量词的命题时,就会得到一个含有存在量词的命题.
试举出社会生活或其他学科中命题的例子,并图示命题及该命题的否定.
解:答案不唯一,举例如下:
命题:高一(3)班所有的女生都是寄宿生.
图示如下:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
