第一章 集合与常用逻辑用语章末小结复习(共30张PPT)
文档属性
| 名称 | 第一章 集合与常用逻辑用语章末小结复习(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 489.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 21:29:06 | ||
图片预览











文档简介
(共30张PPT)
一、系统认知·形成数学思维
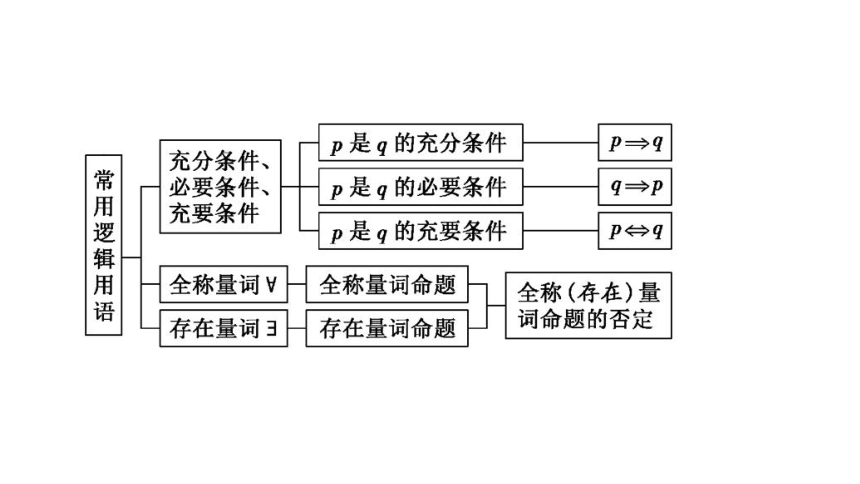
(一)贯通知识体系和联系
(二)把握数学思想和方法
1.在研究集合的关系与运算时,若给定集合是不等式刻画的数集,常用数轴来表示;若给定的集合是具体的数集,常用Venn图来表示;若给定集合是点集,常用坐标系来表示.借助图形来解题,形象直观,体现了数形结合的思想.
2.在含参数的集合中,往往需要对集合的种类和集合中的字母参数进行分类讨论,体现了分类与整合的数学思想.
3.在涉及元素与集合的关系及集合相等的题目,可利用集合中元素相等的概念,列出方程或方程组来解决问题,体现了函数与方程的思想.
4.在解决充分、必要条件问题时,若已知p与q的条件关系,可以转化为集合之间的包含关系,得到方程或不等式求解,体现了化归与转化的思想.
答案:ABD
2.设集合A={x|x2-3x+2=0},则满足A∪B={0,1,2}的集合B的个数是 ( )
A.1 B.3
C.4 D.6
解析:易知A={1,2},又A∪B={0,1,2},所以集合B可以是:{0},{0,1},{0,2},{0,1,2}.
答案:C
3.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是 ( )
A.1 B.3
C.5 D.9
解析:当x=0,y=0时,x-y=0;
当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y=-2;
当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;
当x=1,y=2时,x-y=-1;当x=2,y=0时,x-y=2;
当x=2,y=1时,x-y=1;当x=2,y=2时,x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个.
答案:C
4.已知集合M={1,m+2,m2+4},且5∈M,则m的值为________.
解析:当m+2=5时,m=3,M={1,5,13},符合题意;
当m2+4=5时,m=1或m=-1.
若m=1,M={1,3,5},符合题意;
若m=-1,则m+2=1,不满足元素的互异性,故m=3或1.
答案:3或1
[题型技法]
与集合中的元素有关问题的求解策略
(1)确定集合的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数时,要注意检验集合是否满足元素的互异性.
题型二 集合间的基本关系
1.设P={x|x>4},Q={x|-2A.P Q B.Q P
C.P ( RQ) D.Q ( RP)
解析:因为P={x|x>4},则 RP={x|x≤4},所以Q ( RP).
答案:D
2.已知集合A={x|x2-3x+2=0,x∈R},B={x|0A.1 B.2
C.3 D.4
解析:由x2-3x+2=0得x=1或x=2,∴A={1,2}.由题意知B={1,2,3,4},∴满足条件的C可为{1,2},{1,2,3},{1,2,4},{1,2,3,4}.
答案:D
答案:A
4.已知A={1,4,2x},B={1,x2},若B A,则x的值为________.
解析:由B A,则x2=4或x2=2x.当x2=4时,x=±2,但x=2时,2x=4,这与集合元素的互异性相矛盾;当x2=2x时,x=0或x=2,但x=2时,2x=4,这与集合元素的互异性相矛盾.综上所述,x=-2或x=0.
答案:0或-2
[题型技法]
(1)集合与集合之间的关系是包含和相等的关系,判断两集合之间的关系,可从元素特征入手,并注意代表元素.
(2)根据集合的关系求参数的值或取值范围.
答案:AC
2.已知集合P={x|2A.{x|2C.{x|1解析:由集合P={x|2可得:( RP)∩Q={x|x≤2或x≥4}∩{x|1答案:C
3. 已知全集U=R,集合M={x∈Z|-1≤x-1≤2}和N={x|x=2k+1,k∈N*}的关系如图所示,则阴影部分表示的集合的元素共有 ( )
A.2个 B.3个
C.4个 D.无穷多个
解析:由题意,集合M={x∈Z|-1≤x-1≤2}={x∈Z|0≤x≤3}={0,1,2,3},
N={x|x=2k+1,k∈N*},所以阴影部分表示的集合为( UN)∩M={0,1,2},有3个元素.
答案:B
4.已知集合A={x|x≤a},B={x|1≤x≤2},且A∪( RB)=R,则实数a的取值范围是__________.
解析:因为B={x|1≤x≤2},所以 RB={x|x<1或x>2},又因为A∪ RB=R,所以a≥2.
答案:{a|a≥2}
[题型技法]
集合的运算是指集合间的交、并、补这三种常见的运算,在运算过程中往往由于运算能力差或考虑不全面而出现错误,不等式解集之间的包含关系通常用数轴法,而用列举法表示的集合运算常用Venn图法,运算时特别注意对 的讨论,不要遗漏.
题型四 充分条件与必要条件
1.a>b是a>b+1的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:a>b+1>b得:“a>b+1”可推出“a>b”,而“a>b”不能推出“a>b+1”,
所以a>b是a>b+1的必要不充分条件,故选B.
答案:B
2.已知p:x>2且y>3,q:x+y>5,则p是q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:若x>2且y>3,则x+y>2+3=5,所以p是q成立的充分条件,
当x=1,y=5时,满足x+y>5,但是不满足x>2且y>3,所以p不是q成立的必要条件.
综上所述,p是q成立的充分不必要条件.
答案:A
3.若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为_____.
4.若-a解析:根据充分条件、必要条件与集合间的包含关系,应有{x|-22}.
答案:{a|a>2}
[题型技法]
充分条件、必要条件的三种判定方法
(1)定义法:根据p q,q p进行判断,适用于定义、定理判断性问题;
(2)集合法:根据p,q对应的集合之间的包含关系进行判断,多适用于命题中涉及字母范围的推断问题;
(3)等价转化法:根据一个命题与其逆否命题的等价性进行判断,适用于条件和结论带有否定性词语的命题.
题型五 全称量词命题与存在量词命题
1.命题“ x>0,x2-2x+1≥0”的否定是 ( )
A. x>0,x2-2x+1<0
B. x>0,x2-2x+1<0
C. x≤0,x2-2x+1<0
D. x≤0,x2-2x+1<0
解析:因为命题“ x>0,x2-2x+1≥0”是全称量词命题,全称量词命题的否定是存在量词命题,
所以命题“ x>0,x2-2x+1≥0”的否定是“ x>0,x2-2x+1<0”.故选A.
答案:A
2.(多选)下列命题为假命题的有 ( )
A. x∈R,|x|+1-x=0
B.存在实数x,使x2-2<0
C.若一个四边形的对角线相等,则这个四边形是矩形
D.每一个素数都是奇数
对于C,若平行四边形对角线相等,则该平行四边形是矩形,本题并不是平行四边形而是一般四边形,故不一定为矩形,故C是假命题;
对于D,2是素数,但不是奇数,故D是假命题.
故选A、C、D.
答案:ACD
答案:{m|m≥3} x∈R,+3≠m
4.若对 x∈{x|-2[题型技法]
(1)已知含量词的命题真假求参数的取值范围,实质上是对命题意义的考查.解决此类问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
(2)解决此类问题的关键是根据含量词命题的真假转化为相关数学知识,利用函数、方程、不等式等知识求解参数的取值范围,解题过程中要注意变量取值范围的限制.
一、系统认知·形成数学思维
(一)贯通知识体系和联系
(二)把握数学思想和方法
1.在研究集合的关系与运算时,若给定集合是不等式刻画的数集,常用数轴来表示;若给定的集合是具体的数集,常用Venn图来表示;若给定集合是点集,常用坐标系来表示.借助图形来解题,形象直观,体现了数形结合的思想.
2.在含参数的集合中,往往需要对集合的种类和集合中的字母参数进行分类讨论,体现了分类与整合的数学思想.
3.在涉及元素与集合的关系及集合相等的题目,可利用集合中元素相等的概念,列出方程或方程组来解决问题,体现了函数与方程的思想.
4.在解决充分、必要条件问题时,若已知p与q的条件关系,可以转化为集合之间的包含关系,得到方程或不等式求解,体现了化归与转化的思想.
答案:ABD
2.设集合A={x|x2-3x+2=0},则满足A∪B={0,1,2}的集合B的个数是 ( )
A.1 B.3
C.4 D.6
解析:易知A={1,2},又A∪B={0,1,2},所以集合B可以是:{0},{0,1},{0,2},{0,1,2}.
答案:C
3.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是 ( )
A.1 B.3
C.5 D.9
解析:当x=0,y=0时,x-y=0;
当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y=-2;
当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;
当x=1,y=2时,x-y=-1;当x=2,y=0时,x-y=2;
当x=2,y=1时,x-y=1;当x=2,y=2时,x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个.
答案:C
4.已知集合M={1,m+2,m2+4},且5∈M,则m的值为________.
解析:当m+2=5时,m=3,M={1,5,13},符合题意;
当m2+4=5时,m=1或m=-1.
若m=1,M={1,3,5},符合题意;
若m=-1,则m+2=1,不满足元素的互异性,故m=3或1.
答案:3或1
[题型技法]
与集合中的元素有关问题的求解策略
(1)确定集合的元素是什么,即集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合中元素的个数时,要注意检验集合是否满足元素的互异性.
题型二 集合间的基本关系
1.设P={x|x>4},Q={x|-2
C.P ( RQ) D.Q ( RP)
解析:因为P={x|x>4},则 RP={x|x≤4},所以Q ( RP).
答案:D
2.已知集合A={x|x2-3x+2=0,x∈R},B={x|0
C.3 D.4
解析:由x2-3x+2=0得x=1或x=2,∴A={1,2}.由题意知B={1,2,3,4},∴满足条件的C可为{1,2},{1,2,3},{1,2,4},{1,2,3,4}.
答案:D
答案:A
4.已知A={1,4,2x},B={1,x2},若B A,则x的值为________.
解析:由B A,则x2=4或x2=2x.当x2=4时,x=±2,但x=2时,2x=4,这与集合元素的互异性相矛盾;当x2=2x时,x=0或x=2,但x=2时,2x=4,这与集合元素的互异性相矛盾.综上所述,x=-2或x=0.
答案:0或-2
[题型技法]
(1)集合与集合之间的关系是包含和相等的关系,判断两集合之间的关系,可从元素特征入手,并注意代表元素.
(2)根据集合的关系求参数的值或取值范围.
答案:AC
2.已知集合P={x|2
3. 已知全集U=R,集合M={x∈Z|-1≤x-1≤2}和N={x|x=2k+1,k∈N*}的关系如图所示,则阴影部分表示的集合的元素共有 ( )
A.2个 B.3个
C.4个 D.无穷多个
解析:由题意,集合M={x∈Z|-1≤x-1≤2}={x∈Z|0≤x≤3}={0,1,2,3},
N={x|x=2k+1,k∈N*},所以阴影部分表示的集合为( UN)∩M={0,1,2},有3个元素.
答案:B
4.已知集合A={x|x≤a},B={x|1≤x≤2},且A∪( RB)=R,则实数a的取值范围是__________.
解析:因为B={x|1≤x≤2},所以 RB={x|x<1或x>2},又因为A∪ RB=R,所以a≥2.
答案:{a|a≥2}
[题型技法]
集合的运算是指集合间的交、并、补这三种常见的运算,在运算过程中往往由于运算能力差或考虑不全面而出现错误,不等式解集之间的包含关系通常用数轴法,而用列举法表示的集合运算常用Venn图法,运算时特别注意对 的讨论,不要遗漏.
题型四 充分条件与必要条件
1.a>b是a>b+1的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:a>b+1>b得:“a>b+1”可推出“a>b”,而“a>b”不能推出“a>b+1”,
所以a>b是a>b+1的必要不充分条件,故选B.
答案:B
2.已知p:x>2且y>3,q:x+y>5,则p是q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:若x>2且y>3,则x+y>2+3=5,所以p是q成立的充分条件,
当x=1,y=5时,满足x+y>5,但是不满足x>2且y>3,所以p不是q成立的必要条件.
综上所述,p是q成立的充分不必要条件.
答案:A
3.若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为_____.
4.若-a
答案:{a|a>2}
[题型技法]
充分条件、必要条件的三种判定方法
(1)定义法:根据p q,q p进行判断,适用于定义、定理判断性问题;
(2)集合法:根据p,q对应的集合之间的包含关系进行判断,多适用于命题中涉及字母范围的推断问题;
(3)等价转化法:根据一个命题与其逆否命题的等价性进行判断,适用于条件和结论带有否定性词语的命题.
题型五 全称量词命题与存在量词命题
1.命题“ x>0,x2-2x+1≥0”的否定是 ( )
A. x>0,x2-2x+1<0
B. x>0,x2-2x+1<0
C. x≤0,x2-2x+1<0
D. x≤0,x2-2x+1<0
解析:因为命题“ x>0,x2-2x+1≥0”是全称量词命题,全称量词命题的否定是存在量词命题,
所以命题“ x>0,x2-2x+1≥0”的否定是“ x>0,x2-2x+1<0”.故选A.
答案:A
2.(多选)下列命题为假命题的有 ( )
A. x∈R,|x|+1-x=0
B.存在实数x,使x2-2<0
C.若一个四边形的对角线相等,则这个四边形是矩形
D.每一个素数都是奇数
对于C,若平行四边形对角线相等,则该平行四边形是矩形,本题并不是平行四边形而是一般四边形,故不一定为矩形,故C是假命题;
对于D,2是素数,但不是奇数,故D是假命题.
故选A、C、D.
答案:ACD
答案:{m|m≥3} x∈R,+3≠m
4.若对 x∈{x|-2
(1)已知含量词的命题真假求参数的取值范围,实质上是对命题意义的考查.解决此类问题,一定要辨清参数,恰当选取主元,合理确定解题思路.
(2)解决此类问题的关键是根据含量词命题的真假转化为相关数学知识,利用函数、方程、不等式等知识求解参数的取值范围,解题过程中要注意变量取值范围的限制.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
