2021-2022学年河北省石家庄市正定县第六中学九年级(上)第一次月考数学试卷(Word版 无答案)
文档属性
| 名称 | 2021-2022学年河北省石家庄市正定县第六中学九年级(上)第一次月考数学试卷(Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 06:46:28 | ||
图片预览


文档简介
2021-2022学年河北省石家庄市正定县第六中学九年级(上)第一次月考数学试卷
一、选择题(本大题有16个小题,共42分1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若方程□﹣1=2x是关于x的一元二次方程,则□可以是( )
A.﹣2x B.22 C.x2 D.y2
2.已知x=﹣1是方程x2﹣2x+m=0的一个根,则m的值是( )
A.3 B.﹣3 C.1 D.﹣1
3.2021年正值中国共产党建党100周年,某校开展“敬建党百年,传承红色基因”读书活动.为了了解某班开展的学习党史情况,该校随机抽取了9名学生进行调查,他们读书的本数分别是3、2、3、2、5、1、2、5、4,则这组数据的众数是( )
A.2 B.3 C.3和5 D.5
4.若关于x的方程x2=﹣m有实数根,则m的取值范围是( )
A.m>0 B.m≥0 C.m<0 D.m≤0
5.在比例尺为1:5000000的地图上,甲、乙两地间的图上距离为25厘米,则两地间的实际距离用科学记数法表示为( )
A.1.25×105米 B.12.5×105米 C.1.25×106米 D.1.25×107米
6.如图,BD与CE相交于点A,DE∥BC,DE:BC=2:3,则△ABC与△ADE的面积之比为( )
A.2:3 B.3:2 C.4:9 D.9:4
7.某班在开展“节约每一滴水”的活动中,从全班4名同学中选出10名同学汇报了各自家庭一个月的节水情况,发现节水0.5m3的有2人,水1m3的有3人,节水1.5m3的有2人,节水2m3的有3人,用所学的统计知识估计全班同学的家庭一个月节约用水的总量是( )
A.20m3 B.52m3 C.60m3 D.100m3
8.若是某个一元一次方程的根,则这个一元二次方程可以是( )
A.3x2+2x﹣1=0 B.2x2+4x﹣1=0 C.﹣x2﹣2x+3=0 D.3x2﹣2x﹣1=0
9.如图,AB∥EF,AC=0.5,FC=0.75,若BM、EN分别是△ABC、△CEF的中线,则的值为( )
A. B. C. D.
10.某班级采用小组学习制,在一次数学单元测试中,第一组成员的测试成绩(单位:分)分别为95、90、100、85、95,其中得分85的同学有一道题目被老师误判,其实际得分应该为90,那么该小组的实际成绩与之前成绩相比,下列说法正确的是( )
A.数据的平均数不变 B.数据众数的不变
C.数据的中位数不变 D.数据的方差不变
11.如图,现有甲、乙两种说法
甲:∠B和∠E大小相等
乙:∠C比∠F大
对于这两种说法,正确的是( )
A.甲、乙均正确 B.甲正确,乙错误
C.甲错误,乙正确 D.甲、乙均错误
12.2022年冬季奥运会将在北京张家口举行,如表记录了四名短道速滑选手几次选拔赛成绩的平均数和方差s2.
甲 乙 丙 丁
平均数(单位:秒) 52 m 52 50
方差s2(单位:秒2) 4.5 n 12.5 17.5
根据表中数据,可以判断乙选手是这四名选手中成绩最好且发挥最稳定的运动员,则m、n的值可以是( )
A.m=50,n=4 B.m=50,n=18 C.m=54,n=4 D.m=54,n=18
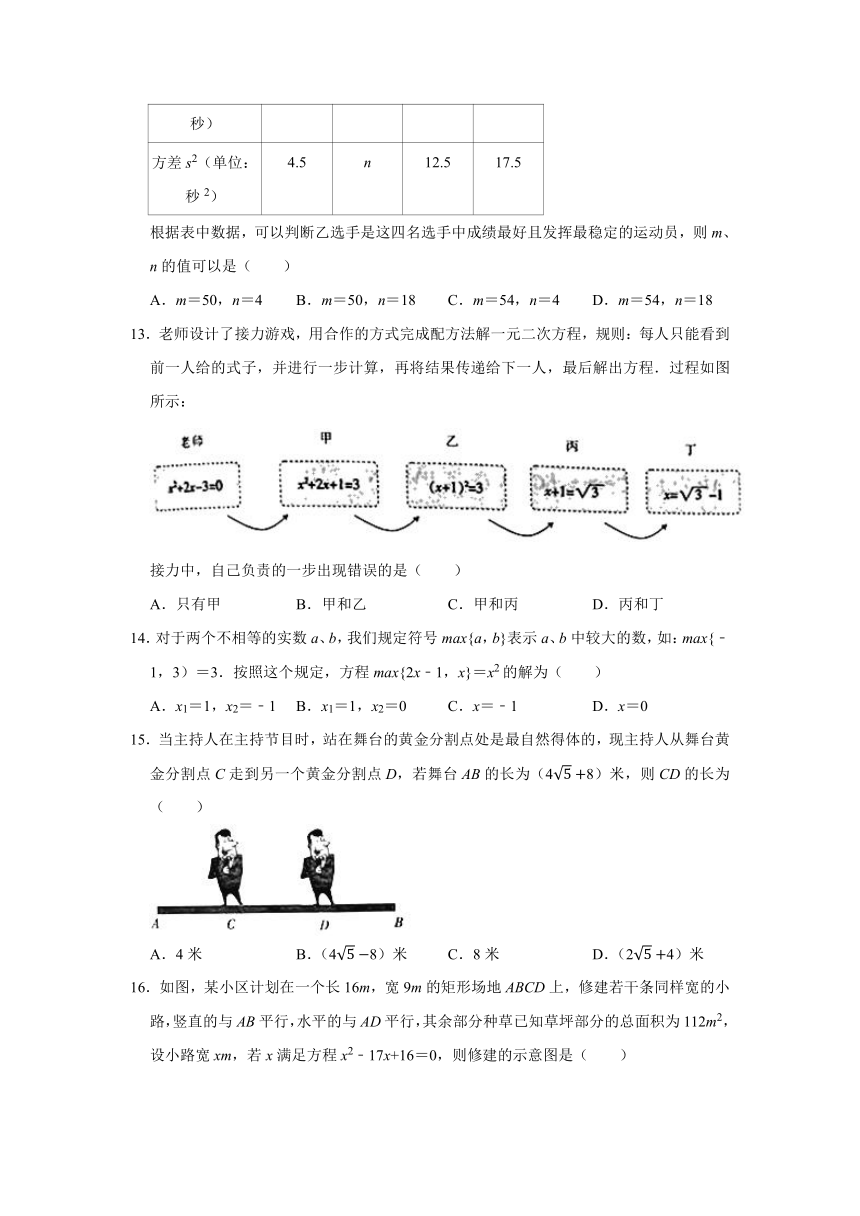
13.老师设计了接力游戏,用合作的方式完成配方法解一元二次方程,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后解出方程.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有甲 B.甲和乙 C.甲和丙 D.丙和丁
14.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{﹣1,3)=3.按照这个规定,方程max{2x﹣1,x}=x2的解为( )
A.x1=1,x2=﹣1 B.x1=1,x2=0 C.x=﹣1 D.x=0
15.当主持人在主持节目时,站在舞台的黄金分割点处是最自然得体的,现主持人从舞台黄金分割点C走到另一个黄金分割点D,若舞台AB的长为(48)米,则CD的长为( )
A.4米 B.(48)米 C.8米 D.(24)米
16.如图,某小区计划在一个长16m,宽9m的矩形场地ABCD上,修建若干条同样宽的小路,竖直的与AB平行,水平的与AD平行,其余部分种草已知草坪部分的总面积为112m2,设小路宽xm,若x满足方程x2﹣17x+16=0,则修建的示意图是( )
A. B.
C. D.
二、填空题(本大题有3个小题,每小题有2个空,每空2分,共12分)
17.把一元二次方程x2=2化成一般形式为 ,其中一次项系数是 .
18.如图,两条直线AC、DF被三条互相平行的直线l1、l2、l3所截,若AB=3,BC=4,请完成以下填空.
(1) .
(2)若AD=5,CF=19,则BE的长为 .
19.魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类证明了勾股定理.已知四边形ABCD、四边形AHGE、四边形DMNE均为正方形,AD=4,CF=3.
(1)DE的长为 .
(2)连接AG交DE于点P,则PE的长为 .
三、解答题(本大题有7个小题,共66分.解答应写出文字说明证明过程或演算步骤)
20.已知有三个数据1,2,3.
(1)求这三个数据的方差s2.
(2)若增加一个数据2,得到的四个数据的方差为s12,则s2 s12.(填“>”、“=”或“<”).
21.已知.
(1)求的值.
(2)求的值.
22.当嘉淇用因式分解法解一元二次方程2x(x﹣1)=1﹣2x时,她是这样做的:
原方程可以化简为2x(2x﹣1)=﹣(2x﹣1),第一步
方程两边同时除以(2x﹣1),得2x=0,第二步
系数化为1,得x=0.第三步
(1)嘉淇的解法是不正确的,她从第 步开始出现了错误.
(2)请用嘉淇的方法完成这个方程的正确解题过程.
23.嘉嘉和淇淇两名同学进行射箭训练,分别射箭五次,部分成绩如折线统计图所示,已知两人这五次射箭的平均成绩相同.
(1)规定射箭成绩不低于9环为“优秀”,求嘉嘉射箭成绩的优秀率.
(2)请补充完整折线统计图;
(3)设淇淇五次成绩的众数为a环,若嘉嘉补射一次后,成绩为b环,且嘉嘉六次射箭成绩的中位数恰好也是a环,求b的最大值.
24.如图所示的是一张白色卡片甲和两张灰色卡片乙、丙,上面分别写有一个整式.现从这三张卡片中进行抽取,规定抽到灰色卡片,就减去上面的整式,抽到白色卡片,就加上上面的整式.
(1)请计算抽到甲、乙两张卡片的结果;
(2)已知抽到甲、丙两张卡片,计算结果的值可能是1吗?请判断并说明理由;
(3)已知同时抽到甲、乙、丙这三张卡片,若计算结果的值为0,请直接写出x的值.
25.某超市连续四次销售某种饮料,已知第一次销售256箱,第二次、第三次的销售量持续增加,第三次的销量达到400箱.
(1)求第二次、第三次这两次销量的平均增长率;
(2)已知该种饮料的进价为每箱25元,第三次的销售价为每箱40元,第四次销售时,若该种饮料每箱每降价1元,销售量就会增加5箱,问当该种饮料每箱降价多少元时,此超市第四次销售该种饮料获利4250元?
26.如图,在矩形ABCD中,AB=6,BC=8,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度运动,过点P作PQ⊥AP,交CD于点Q,交AC于点E,设点P的运动时间为t(0<t<14)s.
(1)填空:AC的长为 .
(2)当点P在AB上时,若S△APE,求四边形PBCQ的面积.
(3)当点P在BC上,∠BAP=45°时,求点P到AC的距离.
(4)当CE时,请直接写出t的取值范围.
一、选择题(本大题有16个小题,共42分1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若方程□﹣1=2x是关于x的一元二次方程,则□可以是( )
A.﹣2x B.22 C.x2 D.y2
2.已知x=﹣1是方程x2﹣2x+m=0的一个根,则m的值是( )
A.3 B.﹣3 C.1 D.﹣1
3.2021年正值中国共产党建党100周年,某校开展“敬建党百年,传承红色基因”读书活动.为了了解某班开展的学习党史情况,该校随机抽取了9名学生进行调查,他们读书的本数分别是3、2、3、2、5、1、2、5、4,则这组数据的众数是( )
A.2 B.3 C.3和5 D.5
4.若关于x的方程x2=﹣m有实数根,则m的取值范围是( )
A.m>0 B.m≥0 C.m<0 D.m≤0
5.在比例尺为1:5000000的地图上,甲、乙两地间的图上距离为25厘米,则两地间的实际距离用科学记数法表示为( )
A.1.25×105米 B.12.5×105米 C.1.25×106米 D.1.25×107米
6.如图,BD与CE相交于点A,DE∥BC,DE:BC=2:3,则△ABC与△ADE的面积之比为( )
A.2:3 B.3:2 C.4:9 D.9:4
7.某班在开展“节约每一滴水”的活动中,从全班4名同学中选出10名同学汇报了各自家庭一个月的节水情况,发现节水0.5m3的有2人,水1m3的有3人,节水1.5m3的有2人,节水2m3的有3人,用所学的统计知识估计全班同学的家庭一个月节约用水的总量是( )
A.20m3 B.52m3 C.60m3 D.100m3
8.若是某个一元一次方程的根,则这个一元二次方程可以是( )
A.3x2+2x﹣1=0 B.2x2+4x﹣1=0 C.﹣x2﹣2x+3=0 D.3x2﹣2x﹣1=0
9.如图,AB∥EF,AC=0.5,FC=0.75,若BM、EN分别是△ABC、△CEF的中线,则的值为( )
A. B. C. D.
10.某班级采用小组学习制,在一次数学单元测试中,第一组成员的测试成绩(单位:分)分别为95、90、100、85、95,其中得分85的同学有一道题目被老师误判,其实际得分应该为90,那么该小组的实际成绩与之前成绩相比,下列说法正确的是( )
A.数据的平均数不变 B.数据众数的不变
C.数据的中位数不变 D.数据的方差不变
11.如图,现有甲、乙两种说法
甲:∠B和∠E大小相等
乙:∠C比∠F大
对于这两种说法,正确的是( )
A.甲、乙均正确 B.甲正确,乙错误
C.甲错误,乙正确 D.甲、乙均错误
12.2022年冬季奥运会将在北京张家口举行,如表记录了四名短道速滑选手几次选拔赛成绩的平均数和方差s2.
甲 乙 丙 丁
平均数(单位:秒) 52 m 52 50
方差s2(单位:秒2) 4.5 n 12.5 17.5
根据表中数据,可以判断乙选手是这四名选手中成绩最好且发挥最稳定的运动员,则m、n的值可以是( )
A.m=50,n=4 B.m=50,n=18 C.m=54,n=4 D.m=54,n=18
13.老师设计了接力游戏,用合作的方式完成配方法解一元二次方程,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后解出方程.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有甲 B.甲和乙 C.甲和丙 D.丙和丁
14.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{﹣1,3)=3.按照这个规定,方程max{2x﹣1,x}=x2的解为( )
A.x1=1,x2=﹣1 B.x1=1,x2=0 C.x=﹣1 D.x=0
15.当主持人在主持节目时,站在舞台的黄金分割点处是最自然得体的,现主持人从舞台黄金分割点C走到另一个黄金分割点D,若舞台AB的长为(48)米,则CD的长为( )
A.4米 B.(48)米 C.8米 D.(24)米
16.如图,某小区计划在一个长16m,宽9m的矩形场地ABCD上,修建若干条同样宽的小路,竖直的与AB平行,水平的与AD平行,其余部分种草已知草坪部分的总面积为112m2,设小路宽xm,若x满足方程x2﹣17x+16=0,则修建的示意图是( )
A. B.
C. D.
二、填空题(本大题有3个小题,每小题有2个空,每空2分,共12分)
17.把一元二次方程x2=2化成一般形式为 ,其中一次项系数是 .
18.如图,两条直线AC、DF被三条互相平行的直线l1、l2、l3所截,若AB=3,BC=4,请完成以下填空.
(1) .
(2)若AD=5,CF=19,则BE的长为 .
19.魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类证明了勾股定理.已知四边形ABCD、四边形AHGE、四边形DMNE均为正方形,AD=4,CF=3.
(1)DE的长为 .
(2)连接AG交DE于点P,则PE的长为 .
三、解答题(本大题有7个小题,共66分.解答应写出文字说明证明过程或演算步骤)
20.已知有三个数据1,2,3.
(1)求这三个数据的方差s2.
(2)若增加一个数据2,得到的四个数据的方差为s12,则s2 s12.(填“>”、“=”或“<”).
21.已知.
(1)求的值.
(2)求的值.
22.当嘉淇用因式分解法解一元二次方程2x(x﹣1)=1﹣2x时,她是这样做的:
原方程可以化简为2x(2x﹣1)=﹣(2x﹣1),第一步
方程两边同时除以(2x﹣1),得2x=0,第二步
系数化为1,得x=0.第三步
(1)嘉淇的解法是不正确的,她从第 步开始出现了错误.
(2)请用嘉淇的方法完成这个方程的正确解题过程.
23.嘉嘉和淇淇两名同学进行射箭训练,分别射箭五次,部分成绩如折线统计图所示,已知两人这五次射箭的平均成绩相同.
(1)规定射箭成绩不低于9环为“优秀”,求嘉嘉射箭成绩的优秀率.
(2)请补充完整折线统计图;
(3)设淇淇五次成绩的众数为a环,若嘉嘉补射一次后,成绩为b环,且嘉嘉六次射箭成绩的中位数恰好也是a环,求b的最大值.
24.如图所示的是一张白色卡片甲和两张灰色卡片乙、丙,上面分别写有一个整式.现从这三张卡片中进行抽取,规定抽到灰色卡片,就减去上面的整式,抽到白色卡片,就加上上面的整式.
(1)请计算抽到甲、乙两张卡片的结果;
(2)已知抽到甲、丙两张卡片,计算结果的值可能是1吗?请判断并说明理由;
(3)已知同时抽到甲、乙、丙这三张卡片,若计算结果的值为0,请直接写出x的值.
25.某超市连续四次销售某种饮料,已知第一次销售256箱,第二次、第三次的销售量持续增加,第三次的销量达到400箱.
(1)求第二次、第三次这两次销量的平均增长率;
(2)已知该种饮料的进价为每箱25元,第三次的销售价为每箱40元,第四次销售时,若该种饮料每箱每降价1元,销售量就会增加5箱,问当该种饮料每箱降价多少元时,此超市第四次销售该种饮料获利4250元?
26.如图,在矩形ABCD中,AB=6,BC=8,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度运动,过点P作PQ⊥AP,交CD于点Q,交AC于点E,设点P的运动时间为t(0<t<14)s.
(1)填空:AC的长为 .
(2)当点P在AB上时,若S△APE,求四边形PBCQ的面积.
(3)当点P在BC上,∠BAP=45°时,求点P到AC的距离.
(4)当CE时,请直接写出t的取值范围.
同课章节目录
