华师大版七年级数学上册4.6.2《角的比较和运算》分层练习(word版含答案)
文档属性
| 名称 | 华师大版七年级数学上册4.6.2《角的比较和运算》分层练习(word版含答案) | 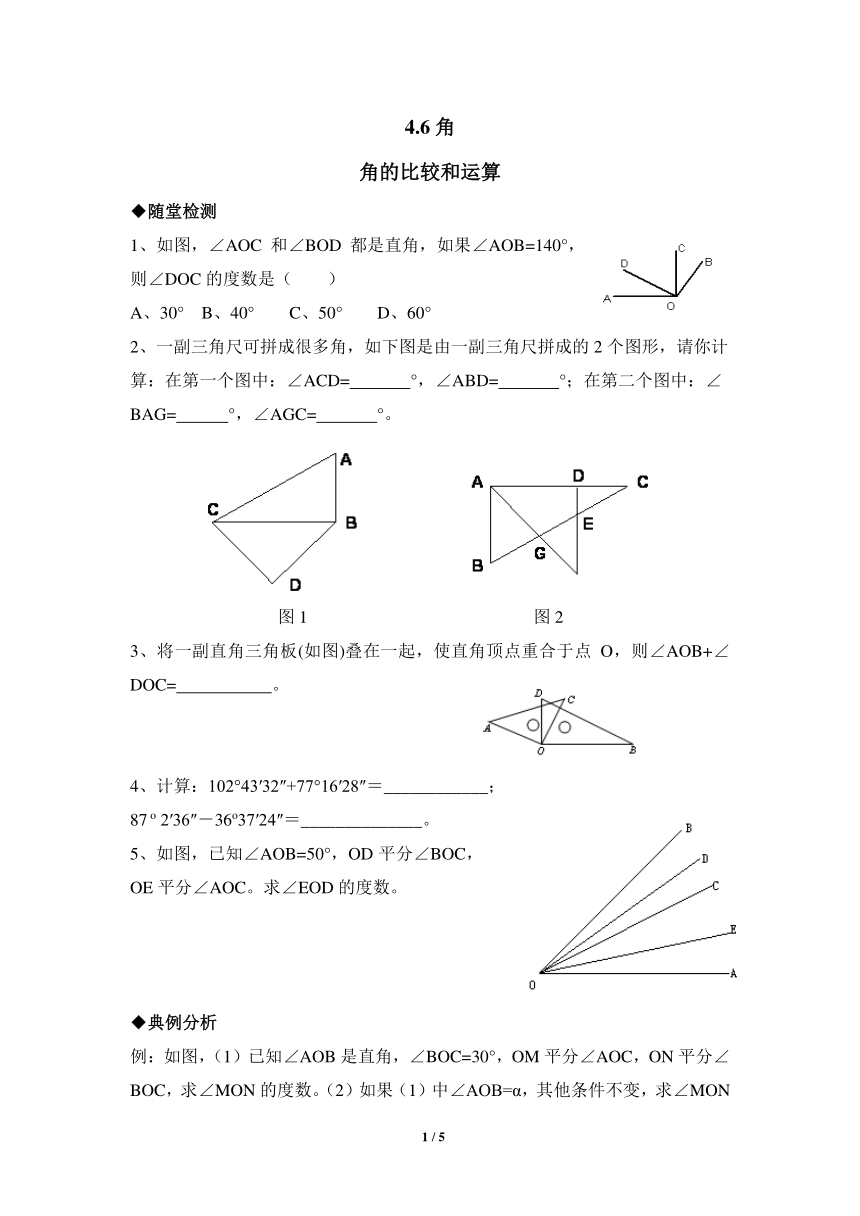 | |
| 格式 | doc | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 10:10:21 | ||
图片预览


文档简介
4.6角
角的比较和运算
◆随堂检测
1、如图,∠AOC和∠BOD都是直角,如果∠AOB=140°,则∠DOC的度数是( )
A、30° B、40° C、50° D、60°
2、一副三角尺可拼成很多角,如下图是由一副三角尺拼成的2个图形,请你计算:在第一个图中:∠ACD= °,∠ABD= °;在第二个图中:∠BAG= °,∠AGC= °。
图1 图2
3、将一副直角三角板(如图)叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 。
4、计算:102°43′32″+77°16′28″=____________;
87 o 2′36″-36o37′24″=______________。
5、如图,已知∠AOB=50°,OD平分∠BOC,OE平分∠AOC。求∠EOD的度数。
◆典例分析
例:如图,(1)已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数。(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数。
(3)你从(1)、(2)的结果中能发现什么规律?
解:(1)∵ OM平分∠AOC,ON平分∠BOC,
∴ ∠MOC=∠AOC,∠NOC=∠BOC
∴ ∠MON=∠MOC-∠NOC=∠AOC-∠BOC=∠AOB
∵ ∠AOB=90°, ∴ ∠MON=45°
(2)当∠AOB=α时,其他条件不变。总有∠MON=∠AOB=
(3)由(1)(2)的结果,可得出结论:∠MON的大小总等于∠AOB的一半。
评析:本例主要是利用角平分线的定义及角和差的意义来解。由特殊从而推断出一般性的规律。
◆课下作业
●拓展提高
1、平面内两个角∠AOB=60°,∠AOC=20°,OA为两角的公共边,则∠BOC为( )
A、40° B、80° C、40°或80° D、无法确定
2、下面一些角中,可以只用一副三角尺(不用量角器)画出来的角是( )
(1)15°的角 (2)65°的角(3)75°的角 (4)135°的角 (5)145°的角
A、(1)(3)(4) B、(1)(3)(5)
C、(1)(2)(4) D、(2)(4)(5)
3、已知:∠A=50°24’,∠B=50.24°,∠C =50°14’24”,那么下列各式正确的是( )
A、∠A>∠B>∠C B、∠A>∠B=∠C
C、∠B>∠C>∠A D、∠B=∠C>∠A
4、如图,BO、CO分别平分∠ABC和∠ACB,已知任意三角形的3个内角的和都是180°,若∠A=80°,你能求出∠BOC的度数吗?试试看。
5、如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD 的平分线,求∠MON的度数。
6、如图,将长方形纸片沿AC折痕对折,使点B落在B′,CF是∠B′CE 平分线,求∠ACF+∠B的度数。
7、如图所示,已知,OE平分,OF平分。
(1)求的度数;
(2)使条件中的,求的度数;
(3)使条件中的,求的度数;
(4)从(1)、(2)、(3)题的结论中你得出了什么结论?
(5)根据这一规律你能编一道类似的关于线段的题目吗
●体验中考
1、(湖北咸宁中考题改编)不重复使用含与含的三角板,能拼画出小于的角的个数为( )
A、 B、 C、 D、
2、(江苏镇江中考题改编)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律?
参考答案
◆随堂检测
1、B 2、75°,135°,45°,105° 3、180°
4、180°,50°25′12″ 5、25°
◆课下作业
●拓展提高
1、C 2、A 3、B 4、∠BOC=90°+∠A=130° 5、45° 6、180°
7、∵,∴。
(1);
(2) =120;
(3) ;
(4)的度数是度数的;
(5)此题开放,答案不惟一。
如:点C是线段AB上一点,D、E分别是线段AC、CB的中点,若DE=,
试求AB的长。
无论如何改变DE的值,均有AB=2DE。
● 体验中考
1、B
2、(1)因OM平分∠AOC,所以∠MOC=∠AOC。
又ON平分∠BOC,所以∠NOC=∠BOC。
所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=∠AOB。
而∠AOB=90°,所以∠MON=45°。
(2)当∠AOB=80°,其他条件不变时,∠MON=×80°=40°。
(3)当∠BOC=60°,其他条件不变时,∠MON=45°。
(4)分析(1)、(2)、(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,而与锐角∠BOC的大小变化无关。
O
A
E
B
F
C
4 / 5
角的比较和运算
◆随堂检测
1、如图,∠AOC和∠BOD都是直角,如果∠AOB=140°,则∠DOC的度数是( )
A、30° B、40° C、50° D、60°
2、一副三角尺可拼成很多角,如下图是由一副三角尺拼成的2个图形,请你计算:在第一个图中:∠ACD= °,∠ABD= °;在第二个图中:∠BAG= °,∠AGC= °。
图1 图2
3、将一副直角三角板(如图)叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 。
4、计算:102°43′32″+77°16′28″=____________;
87 o 2′36″-36o37′24″=______________。
5、如图,已知∠AOB=50°,OD平分∠BOC,OE平分∠AOC。求∠EOD的度数。
◆典例分析
例:如图,(1)已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数。(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数。
(3)你从(1)、(2)的结果中能发现什么规律?
解:(1)∵ OM平分∠AOC,ON平分∠BOC,
∴ ∠MOC=∠AOC,∠NOC=∠BOC
∴ ∠MON=∠MOC-∠NOC=∠AOC-∠BOC=∠AOB
∵ ∠AOB=90°, ∴ ∠MON=45°
(2)当∠AOB=α时,其他条件不变。总有∠MON=∠AOB=
(3)由(1)(2)的结果,可得出结论:∠MON的大小总等于∠AOB的一半。
评析:本例主要是利用角平分线的定义及角和差的意义来解。由特殊从而推断出一般性的规律。
◆课下作业
●拓展提高
1、平面内两个角∠AOB=60°,∠AOC=20°,OA为两角的公共边,则∠BOC为( )
A、40° B、80° C、40°或80° D、无法确定
2、下面一些角中,可以只用一副三角尺(不用量角器)画出来的角是( )
(1)15°的角 (2)65°的角(3)75°的角 (4)135°的角 (5)145°的角
A、(1)(3)(4) B、(1)(3)(5)
C、(1)(2)(4) D、(2)(4)(5)
3、已知:∠A=50°24’,∠B=50.24°,∠C =50°14’24”,那么下列各式正确的是( )
A、∠A>∠B>∠C B、∠A>∠B=∠C
C、∠B>∠C>∠A D、∠B=∠C>∠A
4、如图,BO、CO分别平分∠ABC和∠ACB,已知任意三角形的3个内角的和都是180°,若∠A=80°,你能求出∠BOC的度数吗?试试看。
5、如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD 的平分线,求∠MON的度数。
6、如图,将长方形纸片沿AC折痕对折,使点B落在B′,CF是∠B′CE 平分线,求∠ACF+∠B的度数。
7、如图所示,已知,OE平分,OF平分。
(1)求的度数;
(2)使条件中的,求的度数;
(3)使条件中的,求的度数;
(4)从(1)、(2)、(3)题的结论中你得出了什么结论?
(5)根据这一规律你能编一道类似的关于线段的题目吗
●体验中考
1、(湖北咸宁中考题改编)不重复使用含与含的三角板,能拼画出小于的角的个数为( )
A、 B、 C、 D、
2、(江苏镇江中考题改编)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律?
参考答案
◆随堂检测
1、B 2、75°,135°,45°,105° 3、180°
4、180°,50°25′12″ 5、25°
◆课下作业
●拓展提高
1、C 2、A 3、B 4、∠BOC=90°+∠A=130° 5、45° 6、180°
7、∵,∴。
(1);
(2) =120;
(3) ;
(4)的度数是度数的;
(5)此题开放,答案不惟一。
如:点C是线段AB上一点,D、E分别是线段AC、CB的中点,若DE=,
试求AB的长。
无论如何改变DE的值,均有AB=2DE。
● 体验中考
1、B
2、(1)因OM平分∠AOC,所以∠MOC=∠AOC。
又ON平分∠BOC,所以∠NOC=∠BOC。
所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=∠AOB。
而∠AOB=90°,所以∠MON=45°。
(2)当∠AOB=80°,其他条件不变时,∠MON=×80°=40°。
(3)当∠BOC=60°,其他条件不变时,∠MON=45°。
(4)分析(1)、(2)、(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,而与锐角∠BOC的大小变化无关。
O
A
E
B
F
C
4 / 5
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
